非线性Schrödinger方程的对称约化和精确解

曹 瑞

(菏泽学院 数学系，山东 菏泽 274015)

非线性Schrödinger方程的对称约化和精确解

曹 瑞*

(菏泽学院 数学系，山东 菏泽 274015)

本文研究一类立方非线性Schrödinger方程的对称约化和精确解问题。 首先，利用直接对称方法，得到非线性Schrödinger方程的对称；其次，根据求解相应的特征方程获得非线性Schrödinger 方程的相似约化；最后，结合辅助方程获得非线性Schrödinger方程的精确解。 这些解包括孤立波解、Jacobi椭圆函数解以及三角函数解。

非线性Schrödinger方程的对称；对称约化；精确解；孤立子

作为描述复杂非线性现象的数学模型，非线性发展方程涉及了众多自然科学领域，如物理学，化学，生物，工程等。 非线性发展方程的精确解在解释复杂非线性现象中有着重要作用。 为了寻找非线性发展方程的精确解，许多专家和学者提出了一系列行之有效的求解非线性发展方程精确解的方法，例如齐次平衡法[1]，Painleve截尾展开法[2]，Hirota直接法[3]，sine- cosine方法[4]，双曲函数法[5]，试探函数法[6]，Jacobi椭圆函数展开法[7]以及Jacobi椭圆函数展开方法一般化的F-展开法[8]，G'/G展开法[9，10]，对称约化法[11，12]等。

利用这些方法得到了非线性发展方程许多丰富的精确解，其中包括孤立波解，周期波解，激波解等。

文献[13]中研究了如下非线性Schrödinger方程

其中p，q是非零实常数，ψ=ψ(x，t) 是关于变量x，t的复值函数。 N.Taghizadeh 等运用首次积分方法构造了非线性Schrödinger方程的精确解。 当p=1，q=μ时，我们可以得到文献[14]中的方程，Ma 和Chen 利用直接方法获得了非线性Schrödinger方程的精确解。 在本文中我们讨论如下的立方非线性Schrödinger方程

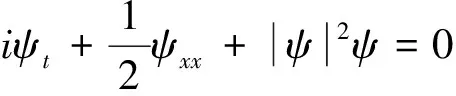
(1)

其中ψ=ψ(x，t)是复函数，i2=-1。 非线性Schrödinger方程(1)与它的各种推广形式在非线性光学、等离子物理以及玻色-爱因斯坦凝聚等领域有着广泛应用[15-17]。 本文的目的是通过直接对称方法寻找非线性Schrödinger方程(1)的精确解。

本文第一部分，介绍直接对称方法的基本思想；第二部分，利用直接对称方法构造非线性Schrödinger方程的对称；然后，根据求解相应的特征方程组得到非线性Schrödinger方程的相似约化；最后，通过一个四阶辅助方程获得了非线性Schrödinger方程的精确解；第三部分，得出一些结论。

1 直接对称方法

下面列出直接对称方法的基本步骤: 对于给定的非线性偏微分方程

F(x，t，u，ut，ux，uxx，…)=0，

(2)

其中F是关于u及其导数的函数。 利用直接对称方法求方程对称的基本步骤为：

第一步：假设方程(2)有下列形式的对称

σ=α(x，t)ut+β(x，t)ux+γ(x，t)u+δ(x，t)，

(3)

其中α，β，γ，δ都是x，t的待定函数，而函数u满足方程(2)。

(4)

将对称(3)代入(4)式，得到关于u的决定方程组，令u的各阶导数系数为零，解的α，β，γ，δ，进而可求得相应的对称σ。

第二步：通过对称σ为零求解一阶偏微分方程，可以得到群不变量。

第三步：利用第二步得到的不变量约化原方程。

2 立方非线性Schrödinger方程的对称约化和精确解

2.1 方程的对称

为了求出方程(1)的对称，我们假定

σ=a(x，t)ψt+b(x，t)ψx+c(x，t)ψ+d(x，t)，

(5)

这里a(x，t)，b(x，t)，c(x，t)，d(x，t) 是待定函数，其中σ满足下面的方程

(6)

将方程(5)代入方程(6)，并考虑方程(1)以及如下方程

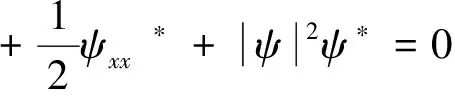
(7)

a(x，t)=2c4t+c2，b(x，t)=c4x-c3t+c1，

c(x，t)=ic3x+ic5+c4，d(x，t)=0。

(8)

其中c1，c2，c3，c4，c5是任意常数。 由此可得所求对称

σ= (2c4t+c2)ψt+(c4x-c3t+c1)ψx+

(ic3x+ic5+c4)ψ，

(9)

其交换图如图1所示。

[σi，σj]σ1σ2σ3σ4σ5σ100σ5σ10σ200-σ12σ20σ3-σ5σ10-σ30σ4-σ1-2σ2σ300σ500000

图1 交换图

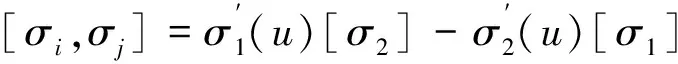
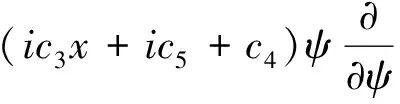
(10)

从向量场(10)，可得对应的五维李代数L={V1，V2，V3，V4，V5} ，有下列一组基

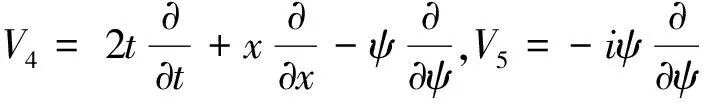
(11)

并且，可以得到与向量场(11)相对应的单参数变换群

g1:(x，t，ψ)→(x+ε，t，ψ)，

g2:(x，t，ψ)→(x，t+ε，ψ)，

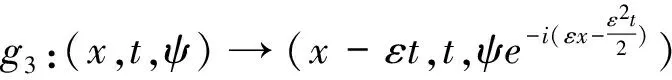
g4:(x，t，ψ)→(eεx，e2εt，e-εψ)，

g5:(x，t，ψ)→(x，t，e-iεψ)。

(12)

这里ε群参数，g1是空间变换 ，g2是时间变换，g3是伽利略变换 ，g4是尺度变换，g5是标量变换。

根据上述单参数群可知，如果f(x，t)是方程(1)的解，那么ψi(i=1，2，3，4，5)也是方程(1)的解。

ψ1(x，t)=f(x-ε，t)，

ψ2(x，t)=f(x，t-ε)，

ψ4(x，t)=e-εf(e-εx，e-2εt)，

ψ5(x，t)=e-iεf(x，t)。

(13)

2.2 方程的对称约化和精确解

本节利用方程σ=0的相容性求方程(1)的对称约化及精确解。 方程(1)的对称σ=(2c4t+c2)ψt+(c4x-c3t+c1)ψx+(ic3x+ic5+c4)ψ。

特征方程为

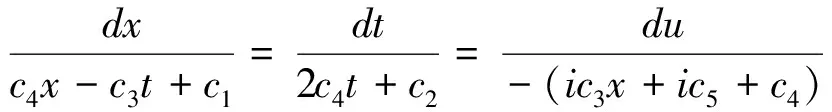
1. 当c1=0，c2=0，c3=0，c4≠0，c5=0时，求解特征方程

可得

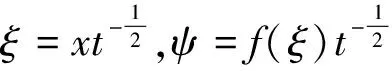
此时，f(ξ)满足方程

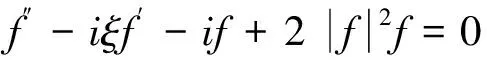
(14)

2.当 c1≠0，c2≠0，c3=0，c4=0，c5≠0时，求解特征方程

可得

ξ=x-vt，ψ=f(ξ)e-iωt。

此时，f(ξ)满足方程

(15)

并且若f(ξ)是上式的解，那么ψ=f(ξ)e-iωt就是方程(1)的解。

下面我们求方程(1)的精确解。 假设

ψ(x，t)=v(x，t)exp(iη)，η=αx+βt，

(16)

其中v(x，t)是实值函数，且α，β是实数。 把(16)代入，方程(1)成为一个实系统

vt+αvx=0，vxx-(α2+2β)v+2μv3=0。

(17)

令v(x，t)=v(ξ)，ξ=k(x-αt)，k≠0。方程(17)可化为

k2v″-(α2+2β)v+2μv3=0，

(18)

上式乘以2v′积分一次得到

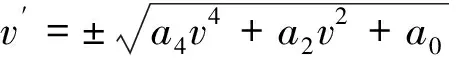
(19)

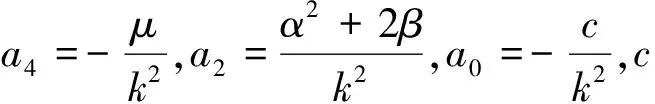
情形1 Jacobi椭圆函数解

(1.1)当a0=1，a2=-(1+m2)，a4=m2时，

ψ1=eiηsn(ξ)，ψ2=eiηcd(ξ)。

(1.2)当a0=1-m2，a2=2m2-1，a4=-m2时，v(ξ)=cn(ξ)， 此时

ψ3=eiηcn(ξ)。

(1.3)当a0=m2-1，a2=2-m2，a4=-1时，v(ξ)=dn(ξ)，此时

ψ4=eiηdn(ξ)。

(1.4)当a0=m2，a2=-(1+m2)，a4=1时，

ψ5=eiηns(ξ)，ψ6=eiηdc(ξ)。

(1.5)当a0=-m2，a2=2m2-1，a4=1-m2时，

ψ7=eiηnc(ξ)。

(1.6)当a0=-1，a2=2-m2，a4=m2-1时，v(ξ)=nd(ξ)， 此时

ψ8=eiηnd(ξ)。

(1.7)当a0=1，a2=2-m2，a4=1-m2时， v(ξ)=sc(ξ)，此时

ψ9=eiηsc(ξ)。

(1.8)当a0=1，a2=2m2-1，a4=-m2(1-m2)时，v(ξ)=sd(ξ)，此时

ψ10=eiηsd(ξ)。

(1.9)当a0=1-m2，a2=2-m2，a4=1时，v(ξ)=cs(ξ)，此时

ψ11=eiηcs(ξ)。

(1.10)当a0=-m2(1-m2)，a2=2m2-1，a4=1时，v(ξ)=ds(ξ)，此时

ψ12=eiηds(ξ)。

ψ13=eiη(ns(ξ)±cs(ξ))。

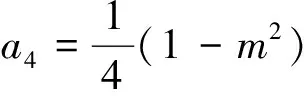
ψ14=eiη(nc(ξ)±sc(ξ))。

ψ15=eiη(ns(ξ)±ds(ξ))。

ψ16=eiη(sn(ξ)±icn(ξ))。

情形2 三角函数解

(2.3)当m→0时，情形1中的椭圆函数解ψ9退化三角函数解

ψ19=eiηtan(ξ)。

情形3 孤立子解

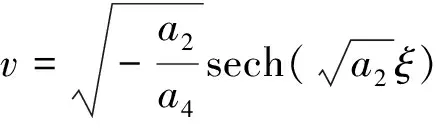
(3.3)当m→1时，情形1中的椭圆函数解ψ3退化亮孤子解

ψ22=eiηsech(ξ)。

(3.4)当m→1时，情形1中的椭圆函数解ψ1退化暗孤子解

ψ23=eiηtanh(ξ)。

注：(1)当模m→1时，Jacobi椭圆函数退化为双曲函数。

snξ→tanhξ，cnξ→sechξ，scξ→sinhξ，

csξ→cschξ，ncξ→coshξ。

(2)当模m→0时，Jacobi椭圆函数退化为三角函数。

snξ→sinξ，cnξ→cosξ，scξ→tanξ，csξ→cotξ，

ncξ→secξ，nsξ→cscξ。

3 结语

本文把直接对称方法应用于具有重要物理背景的立方非线性Schrödinger方程，成功得到了立方非线性Schrödinger方程的对称。 并根据所得对称相应的特征方程求出了方程的不变量和相似约化。 再通过行波约化，结合四阶辅助方程获得了立方非线性Schrödinger方程的丰富的精确解，这些解包括孤立波解、Jacobi椭圆函数解以及三角函数解。当Jacobi椭圆函数解中参数取特殊值时可以得到双曲函数解、孤立波解。 这些精确解丰富了立方非线性Schrödinger方程精确解的解系，同时，由于该方程是光学中的重要方程，这些得到的精确解将有助于物理上对该方程的研究。

[1] WANG M L，ZHOU Y B，LI Z B. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J]. Phys Lett A，1996，216:67-75.

[2] 张解放，陈芳跃.截断展开方法和广义变系数Kdv方程[J].物理学报，2001，50(9):1648-1650.

[3] Hirota R. The Direct Methods in Soliton Theory[M].Cambridge:Cambridge University，2004.

[4] Yan C T. A simple transformation for nonlinear waves[J].Phys Lett A，1996，224:77-84.

[5] 郭冠平，张解放. 关于双曲函数方法求孤波解的注记[J]. 物理学报，2002，51(6):1159-1162.

[6] Cao Rui，Zhang Jian.Trial function method and exact solutions to the generalized nonlinear Schrödinger equation with time- dependent coefficient[J].Chinese Physics B，2013，22(10):100507-1-100507-4.

[7] 向以华，石义霞. (2+1)维色散长波方程的扩展椭圆函数有理展开解法[J]. 数学杂志，2009(2):206-210.

[8] 曹瑞. 改进的F-展开方法和藕合Klein- Gordon方程的精确解[J]. 兰州大学学报(自然科学版)，2007，43(6):112-116.

[9] BIAN Chunquan，PANG Jing，JIN Linghua，et al. Solving two fifth order strong nonlinear evolution equations by using the (G/G')- expansion method[J]. Communications in Nonlinear Science and Numerical Simulation，2010，15(9):2337-2343.

[10] 李帮庆，马玉兰. G/G'展开法和(2+1)维非对称Nizhnik- Novikov- Veselov系统的新精确解[J].物理学报，2009，58(7):4373-4378.

[11] MIAO Q，XIN X P，CHEN Y. Nonlocal symmetries and explicit solutions of the AKNS system[J]. Applied Mathematics Letters，2014，28:713.

[12] CHEN J C，XIN X P，CHEN Y. Symmetry Analysis and Conservation Laws to the (2+1)- Dimensional Coupled Nonlinear Extension of the Reaction- Diffusion Equation[J]. Commun Theor Phys， 2014，62:173-182.

[13] Taghizadeh N，Mirzazadeh M，Farahrooz F. Exact solutions of the nonlinear Schrödinger equation by the first integral method[J]. J Math Anal Appl， 2011，374:549-553.

[14] MA W X，CHEN M. Direct search for exact solutions to the nonlinear Schrödinger equation[J]. Appl Math Comput， 2009，215:2835-2842.

[15] Zabusky N J，Kruskal M D. Interaction of "soliton" in a collisionless plasma and the recurrence of initial states[J]. Phys Rev Lett，1965，19:1095-1097.

[16] Ablowitz M J，Segur H. Solitons and the Inverse Scattering Transformation[M]. Philadelphia:SIAM，1981.

[17] Hasegawa A，Kodama Y. Solitons in Optical Communications[M].New York:Oxford University Press，1995.

[18] 刘式适，刘式达.物理学中的非线性方程[M].北京: 北京大学出版社，2000.

(责任编辑：周晓南)

Symmetry Reduction and Exact Solutions of Nonlinear Schrödinger Equation

CAO Rui*

(Department of Mathematics, Heze University, Heze 274000, China)

Symmetry of nonlinear Schrödinger equation was investigated. Applying direct symmetry method, symmetry of nonlinear Schrödinger equation was derived. By solving corresponding characteristic equation associated with the symmetry equation, symmetry reduction of nonlinear Schrödinger were obtained based on a fourth- order auxiliary equation, these solutions include solitary wave solutions, Jacobi elliptic function solutions and trigonometric function solutions.

nonlinear Schrödinger equation; direct symmetry method; exact solution; soliton

1000-5269(2016)06-0001-04

10.15958/j.cnki.gdxbzrb.2016.06.01

2016-05-30

国家自然科学基金项目资助(11347102，11401409)；山东省自然科学基金项目资助(ZR2011AL018，ZR2011AQ008)；山东省高校科技计划项目资助(J13LI02)；荷泽学院自然科学基金项目资助(xy14KJ04)

曹瑞(1979-)，女，副教授，研究方向: 孤立子和可积系统，Email:ruicao999@126.com.

曹瑞，Email:ruicao999@126.com.

O175.2

A