扩张矩阵的一些性质

孙瑞瑞,李金霞

(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)

扩张矩阵的一些性质

孙瑞瑞,李金霞

(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)

研究了相关于扩张矩阵A的扩张球和拟范数的一些性质.首先通过具体实例及欧氏范数关于A的上下界估计指出扩张矩阵与经典球及欧氏范数匹配不佳,但欧氏范数相关于A仍能保持全局伸缩性.其次研究了相适应于扩张矩阵的扩张球和拟范数关于伸缩性、凸性、可积性、微分估计及傅里叶变换的一些性质.最后通过欧氏范数与相关于扩张矩阵的拟范数的不等式估计证明了相关于拟范数的两类施瓦茨函数空间和相关于欧氏范数的经典施瓦茨函数空间都是等价的.

各向异性;扩张矩阵;扩张球;施瓦茨函数空间

1 引言

各向异性是自然界物体的一种常见属性,亦称“非均质性”,指物体的全部或部分物理、化学等性质随方向的不同而各自表现出一定的差异的特性.如晶体的各向异性具体表现在不同方向上的弹性模量、硬度、断裂抗力、屈服强度等都是不同的.在数学上可将各向异性通过离散伸缩群{Ak:k∈Z}来表达,其中A为特征值的模均严格大于1的实n×n矩阵,这样的A被称作是扩张矩阵.目前,有许多学者致力于研究各向异性的函数空间、小波及相关算子的有界性;参见文献[1-5].然而,扩张矩阵A与欧氏范数和经典球匹配的不是很好.因此,Bownik在文献[1],中引入了一类新的扩张球和拟范数来匹配这样的离散伸缩群{Ak:k∈Z}.在本文中,研究了相关于扩张矩阵A的扩张球和拟范数的一些性质.

为了方便起见,对全文做如下约定.|·|定义为Rn上的欧氏范数.N:={0,1,2,···}.Z代表整数集.对任意的α:=(α1,···,αn)∈Nn,记|α|:=α1+···+αn.设C是与主要变量无关的常量,它在不同行会表示不同的值.我们用记号D≾F来表示D≤CF.如果D≾F且F≾D,那么记做D～F.对任意的集合E⊂Rn,χE表示集合E的特征函数.

2 概念和主要结果

在数学上各向齐性的一些性质可以推广到各向异性的情况下.例如,设

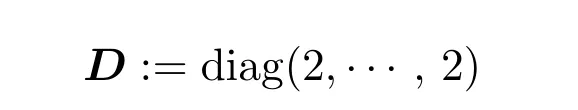
是Rn上的一个数量矩阵,φ∈L1(Rn)且满足

对所有的k∈Z和x∈Rn,记φ2k(x):=|detD|kφ(Dkx)是φ上的一个各向齐性伸缩,则对任意的p∈[1,∞]及任意给定的 f∈Lp(Rn),对几乎处处的x∈Rn,当 k→+∞时,有

一般情况下,设A是一个扩张矩阵,用各向异性伸缩群{Ak:k∈Z}来代替各向齐性伸缩群{Dk:k∈Z}时,(1)式仍然成立(参见文献[1]).设λ−,λ+是满足如下条件的两个正数：

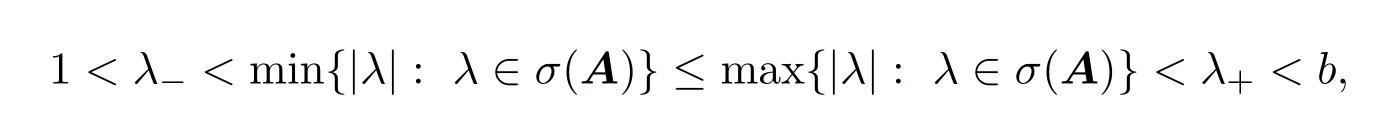
其中σ(A)定义为扩张矩阵A的全体特征值所组成的集合.在本文中,记b:=|detA|.若扩张矩阵A在复数域C上可对角化,则定义

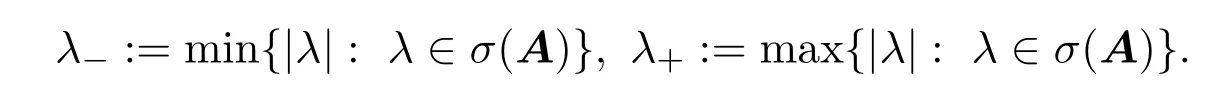
注2.1(i)扩张矩阵A和范数|·|不太匹配.例如,当用各向异性的伸缩来代替各向齐性的伸缩时,范数|·|不一定具有齐次性.即:对任意的x∈Rn和k∈Z,|Dkx|n=|detD|k|x|n,但是当A不是数量矩阵时,|Akx|n=|detA|k|x|n不一定成立.

(ii)当扩张矩阵A与范数|·|或Rn中的球相作用时,它的局部伸缩性不是很好.下面,将给出两个例子:

(a)对任意的扩张矩阵A和任意的x∈Rn,|Ax|＞|x|不一定成立.例如,取n=2, x=(1,1)且

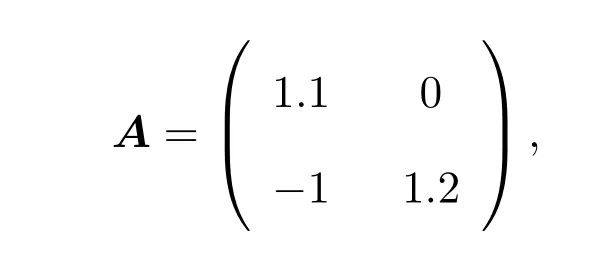
但|Ax|＜|x|.

(b)设0n:=对任意的球

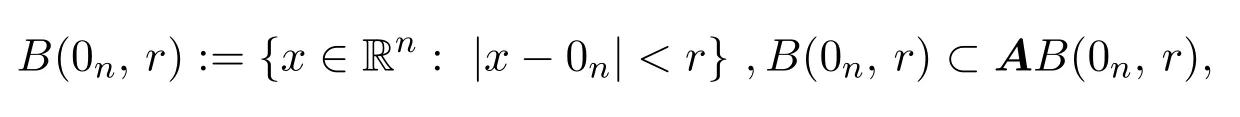
不一定成立,其中 r∈(0,+∞).例如,取B(0n,r)=B(0n,1)和

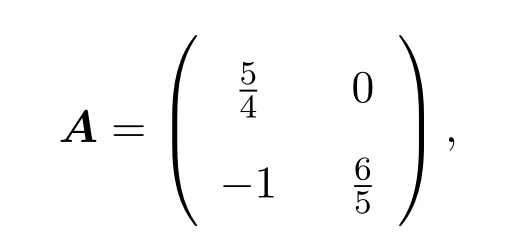
断言B(0n,1)AB(0n,1).事实上,设x1=则x1∈B(0n,1).若存在某个B(0n,1),使得则

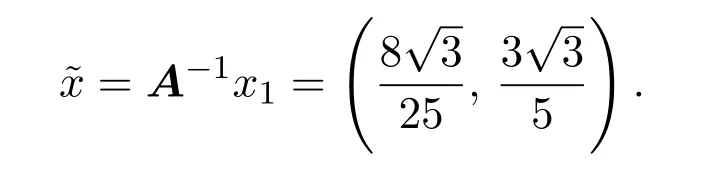
类似地,A−1B(0n,r)⊂B(0n,r)也不一定成立.

(iii)扩张矩阵A具有全局伸缩性.也就是说,对于任意的x∈Rn和j∈Z,

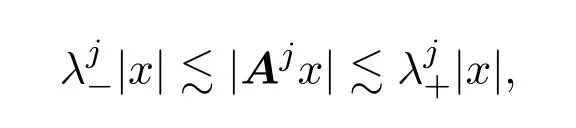
当j→+∞时,

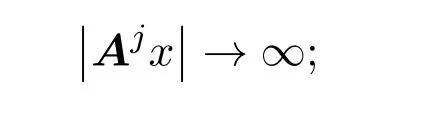
当j→−∞时,

因此,Bownik[1]引进了一类新的适应于扩张矩阵A的扩张球和拟范数.对一个给定的扩张矩阵A,存在一个实数r∈(1,∞)和一个开的椭球

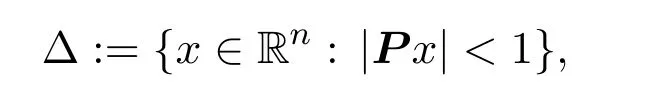
使得Δ⊂rΔ⊂AΔ,其中P是一个非退化的n×n矩阵.通过一个标量变更,不妨设|Δ|=1,其中|Δ|定义为Δ的n维勒贝格测度.设Bk:=AkΔ,k∈Z.那么Bk是开的,

并且|Bk|=bk.设E是Rn的任意子集,记EC:=RnE并且E+F定义为E⊂Rn上的代数和{x+y:x∈E,y∈F}.对任意的k,j∈Z且k≤j,以下结论成立(参见文献[1]):

其中σ是使得2B0⊂AσB0=Bσ的最小正整数.

定义 2.1若ρA:Rn→[0,∞)满足以下条件,则被称为是伴随于扩张矩阵A的拟范数:

(i)对任意x∈Rn{0n},有ρA(x)＞0;

(ii)对任意x∈Rn,ρA(Ax)=bρA(x),其中b:=|detA|;

(iii)对任意x,y∈Rn,ρA(x+y)≤H[ρA(x)+ρA(y)],其中H ∈[1,∞)是一个不依赖于x和y的常数.

这里,给出拟范数的一些例子:

(i)在标准情形A:=2In×n和ρA(x):=|x|n下,对所有的x∈Rn,ρA是一个相关于扩张矩阵A的拟范数的例子.

(ii)相关于扩张矩阵A的阶梯拟范数ρ定义为：

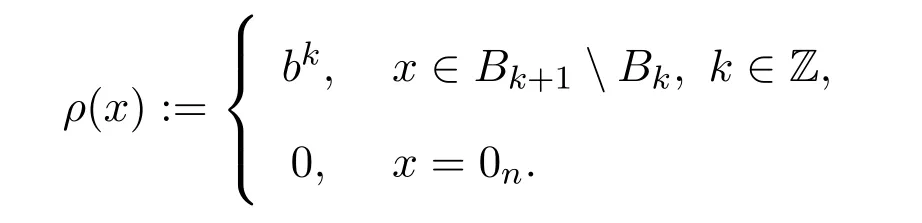
由(3)式,可以得到,对所有的x,y∈Rn,

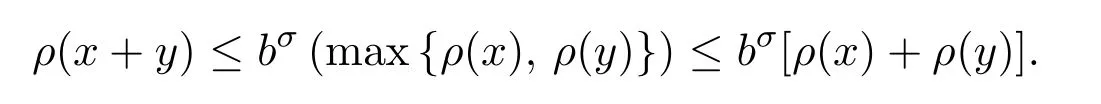
显然,ρ是一个拟范数,并且由这个拟范数ρ衍生出的ρ-球{x∈Rn:ρ(x)＜r}是凸的(参见命题2.1(ii)).此外,由文献[6]可知测度空间(Rn,ρ,dx)是一个齐型空间,其中dx表示n维勒贝格测度.

(iii)Bownik在文献[3]中指出

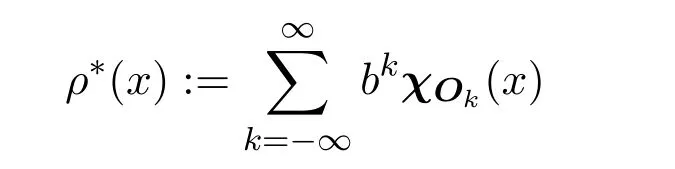
也是一个拟范数,其中

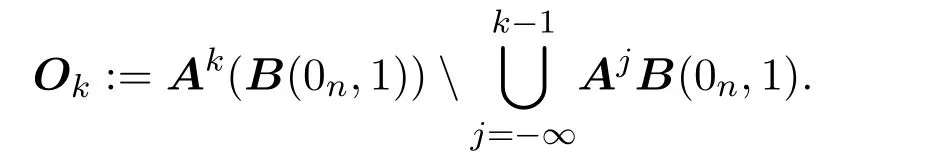
此外,Bownik还指出由这个拟范数ρ∗衍生出的ρ∗-球{x∈Rn:ρ∗(x)＜r}却不一定是凸的.但此类球与A进方体集{Aj([0,1)n+k):j∈Z,k∈Zn}有很好的几何关系,具体内容参见文献[3].

Bownik在文献[1]中证明了相关于一个固定的扩张矩阵的任何两个拟范数都是等价的.为方便起见,全文将固定使用阶梯拟范数ρ.

在本文中,为方便起见,定义B:={x+Bk:x∈Rn,k∈Z}.

注2.2(i)由定义2.1(ii),知道任意一个相关于扩张矩阵A的拟范数ρ都具有齐次性;

(ii)用拟范数ρ和扩张球集B来与扩张矩阵A作用时,A具有很好的伸缩性.

(a)由定义2.1(ii)和b＞1,可以得到,对于相关于A的任意拟范数ρ和x∈Rn,

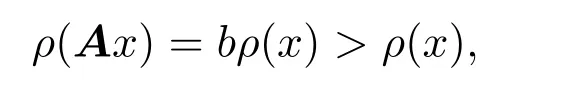
这意味着相关于A的拟范数ρ比欧氏范数扩张性好;

(b)由(2)式,对任意的x0∈Rn和k∈Z,有x0+Bk⊂x0+ABk.

此外,对扩张矩阵A有如下的一些性质.

命题 2.1设A是一个扩张矩阵,B∈B且ρ是一个相关于A的拟范数.

(i)|AB|=b|B|.

(ii)B是凸的且对任意的x∈Bk,k∈Z,有−x∈Bk.

(iii)设ϕ是一个局部可积函数,则对任意的扩张球x0+Bk,有

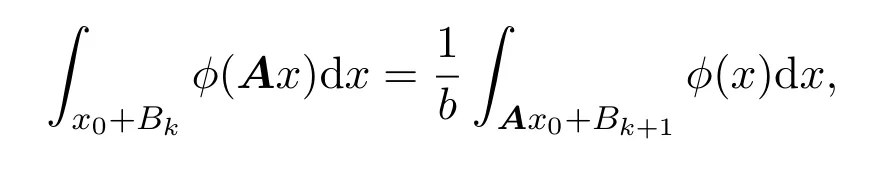
其中x0∈Rn且k∈Z.

(iv)任给ϕ∈L1(Rn),记为ϕ的傅里叶变换且ϕk(x):=bkϕ(Akx),其中x∈Rn,k∈Z,则对任意的ξ∈Rn,有

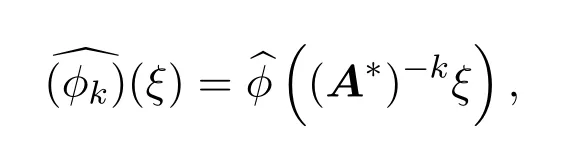
其中A∗表示A的转置矩阵.

(v)对任意的α∈Nn及α阶可微函数ϕ,存在正常数C对任意x∈Rn,有

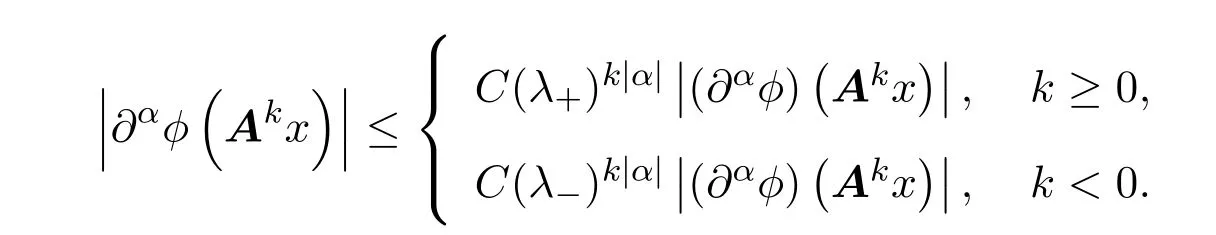
(vi)对任意的ε∈(0,∞),有

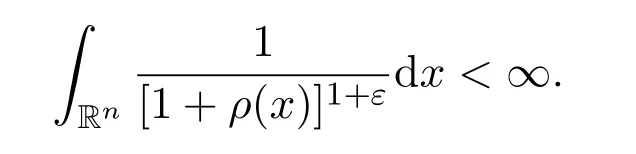
证明(i)设B:=x0+Bk,其中x0∈Rn,k∈Z.由Bk=AkΔ,|x0+Bk|=|Bk|和AB=Ax0+ABk=Ax0+Bk+1,得到

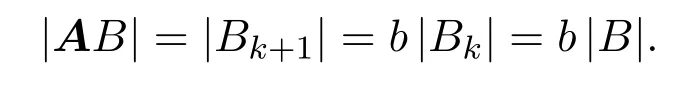
(ii)要证B是凸的,只需证明,对任意的x,y∈B和θ∈(0,1),θx+(1−θ)y∈B.事实上,对x∈B:=x0+Bk,因为Bk=AkΔ,所以存在某个Δ使得x=由＜1,我们有类似地,对y∈B,存在某个Δ使得y=且因此,

即证得B是凸的.

对任意的x∈Bk,因为Bk=AkΔ,所以存在某个∈Δ使得x=则Δ,进而可得−x∈Bk.

(iii)设y=Ax,则x=A−1y,dx=b−1dy且y∈Ax0+Bk+1.因此,

(iv)对任意的ϕ∈L1(Rn)和ξ∈Rn,

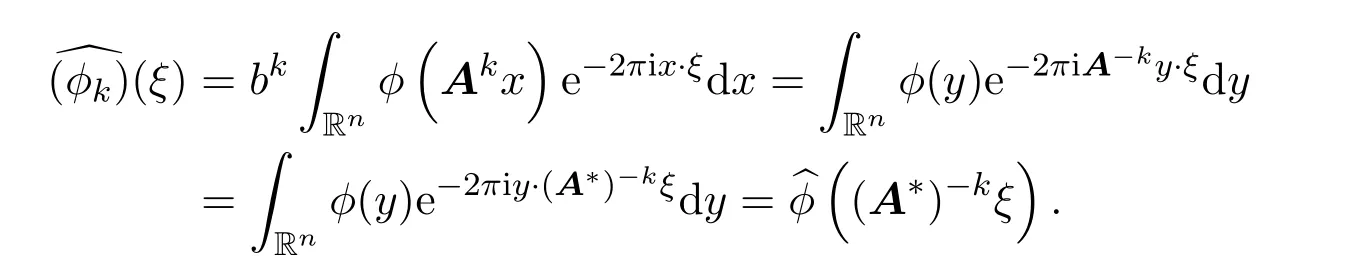
(v)详见文献[1].

(vi)对任意的ε∈(0,∞),

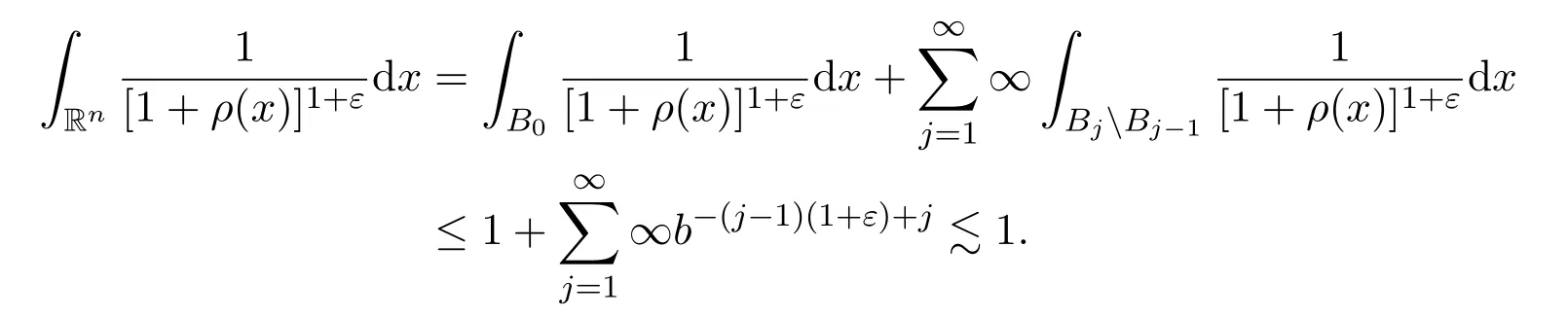
对任意的ϕ∈C∞(Rn),α∈Nn和设

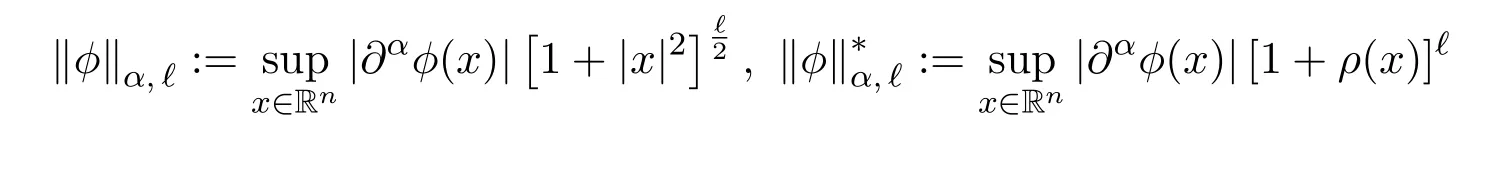
及

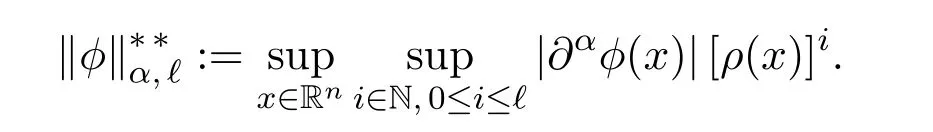
对相关于拟范数ρ的施瓦茨函数空间和相关于欧氏范数|·|的经典施瓦茨函数空间有以下定理.

定理 2.1S(Rn)=S∗(Rn)=S∗∗(Rn).

要证定理2.1,需要下面来自于文献[1]中的引理.

引理 2.1对于任意的x∈Rn,存在一个正常数C使得:

定理2.1的证明由引理2.1和λ+≥λ−＞1知,对任意的α∈Nn和N,有

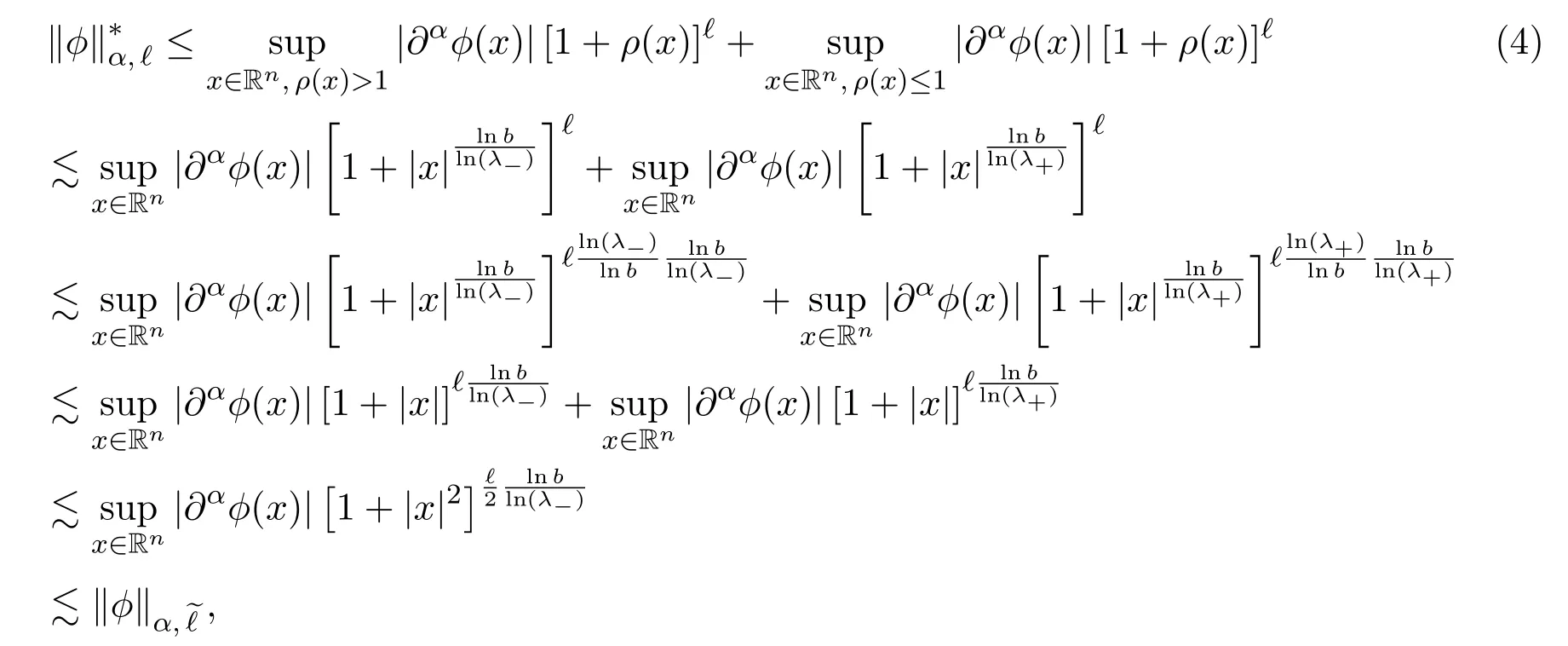
由上式和(4)式可得S(Rn)=S∗(Rn).

此外,

注2.3Bownik在文献[1]中也提到了类似于S(Rn)=S∗∗(Rn)的性质,但是没有给出证明,在定理2.1中给出了证明.

[1]Bownik M.Anisotropic Hardy spaces and wavelets[J].Mem.Amer.Math.Soc.,2003,164:781.

[2]Barrios B,Betancor J J.General characterizations of anisotropic Besov spaces[J].Publ.Math.Debrecen, 2012,80(1-2):179-198.

[3]Bownik M,Ho K P.Atomic and molecular decompositions of anisotropic Triebel-Lizorkin spaces[J].Tran. Amer.Math.Soc.,2005,358(4):1469-1510.

[4]Bownik M,Li B D,Yang D C,etal.Weighted anisotropic Hardy spaces and their applications in boundedness of sublinear operators[J].Indiana Univ.Math.J.,2008,57(7):3065-3100.

[5]Liu J,Yang D C,Yuan W.Anisotropic Hardy-Lorentz spaces and their applications[J].Sci.China Math., 2016,59(9):1669-1720.

[6]Coifman R R,Weiss G.Extensions of Hardy spaces and their use in analysis[J].Bull.Amer.Math.Soc., 1977,83(4):569-645.

Some properties of expansive matrix

Sun Ruirui,Li Jinxia
(College of Mathematics and System Science,Xinjiang University,Urumuqi830046,China)

In this paper,we study some properties of dilated balls and quasi-norms associated with expansive matrix A.Firstly,we point out that expansive matrix can not match very well with classical balls and Euclidean norm via some specific examples and the bounded estimates of Euclidean norm associated with A,but the Euclidean norm still maintains the global flexibility associated with A.Secondly,we study some properties about dilated balls and quasi-norm associated with A in terms of flexibility,convexity,integrability,differential estimate and Fourier transform.Finally,we prove that two kinds of Schwartz function spaces associated with the corresponding quasi-norms are equivalent with the classical Schwartz function space.

anisotropic,expansive matrix,dilated ball,Schwartz function space

O174.2

A

1008-5513(2017)02-0160-08

10.3969/j.issn.1008-5513.2017.02.007

2016-11-11.

国家自然科学基金(11461065);新疆维吾尔自治区青年博士培养计划(qn2015bs003).

孙瑞瑞(1989-),硕士生,研究方向:调和分析.

李金霞(1991-),硕士生,研究方向:调和分析.

2010 MSC:42B35