不确定单机排序的一个新的双目标模型和算法①
张 敏 张兴芳
(1.中央筹备粮聊城直属库,山东聊城252000; 2.聊城大学数学科学学院,山东聊城252059)
不确定单机排序的一个新的双目标模型和算法①
张 敏1张兴芳2
(1.中央筹备粮聊城直属库,山东聊城252000; 2.聊城大学数学科学学院,山东聊城252059)
在单机排序问题中,假设一些任务被分成若干组(称为链),它们分别有一个交货截止日期和权重,任务的处理时间具有不确定性,又缺乏历史的数据.以往人们关心任务链如何排序使得耽误任务的总加权数最小或任务的加权完成时间最小或它们同时最小.本文首先基于不确定理论,视任务的处理时间为不确定变量,建立了一个新的双目标整数规划模型. 然后给出了其模型的性质.
单机排序, 耽误任务总加权数, 最后一个按时完工时间, 不确定理论
0 引言
现实生活中经常遇到任务的各种排序问题.本文研究下述的单机排序问题.假设一个供应商要在一个机器上依次处理一些代理商的任务.每两个相邻任务无耽搁时间.在每个时刻,机器仅能处理一个任务.每个任务在机器上仅需要处理一次.代理商分别要求一定的交货截至日期.又假定供应商能够基于自己当前的利益和长远的利益,各代理商的任务的数量和重要程度分别赋予各代理商一定的权重.本文关心如何将这些任务进行排序使得耽误任务总加权数和最后一个按时完工的任务的完成时间同时最小.
易见, 上述问题的解(最优排序)具有每个代理商的任务组不打断的特征. 所以该问题是不中断的链单机排序问题1|chans|∑ωjUj.如果将 每个 代理商 的任务组(称链) 看做一个任务,耽误任务的总加权数可归结为问题1|∑ωjUj.本文又同时考虑最后一个按时完工的链时间最短. 因此,这是一个双目标整数规划问题.
关于单机排序的早期研究者有Smith[1]. 他们指出该问题是一个NP(non-deterministicpolynomial-time)-难问题. 因此,在近六十年里, 许多学者对此模型的算法进行了大量的研究[2-9].
关于单机排序问题的早期研究都假定任务的处理时间是一个常数[1-7]. 然而,客观现实往往并非如此.于是,随着概率论的问世,一些学者将任务的处理时间看作随机变量,应用概率论解决此类问题[8]. 注意,概率论应用的前提要有大量的历史数据.当缺乏历史数据时,于是人们采用专家赋予不确定数据信度的方法.有的学者认为这是主观概率. 然而,在主观概率下,独立事件的概率乘积运算法则得到的结果和人们直觉的结果往往不一致,如P(A∩B)=P(A)×P(B)=0.5×0.5=0.25.这里数值0.25太小,往往人们不能接受它.后来,1965年,Zadeh提出了 模糊集理论.自然地,有些学者将其应用到此问题中[9]. 在2007年,刘宝碇又基于正规性公理,对偶性公理和次可加性公理,提出了一种新的处理缺乏历史数据的不确定性的数学理论,称为不确定理论[10].2010年后他又进行了补充和完善[11,12].如今,已经形成它的许多数学分支,如不确定规划[13],不确定逻辑[14],不确定过程[15]等.本文将应用刘的不确定理论研究上述的单机排序问题.
注意,以往学者们关心这些任务链如何排序使得耽误任务的总加权数最小或任务的加权完成时间最小或它们同时最小.而本文关心耽误任务的总加权数和最后一个按时完工时间同时最小.这种情况在实际中也是时常见到的.截止目前,作者未见这种研究.
以下的组织结构如下:第二节介绍下文用到的不确定理论的基本知识.第三节,基于不确定理论,将任务的处理时间看作具有不确定分布的不确定变量,建立耽误任务的总加权数和最后一个按时完工时间同时最小模型.第四节研究其模型的性质.最后一节概括本文的主要结果.
1 准备
本节介绍下文用到的不确定理论的基本知识[10-12]和双目标规划模型的有效解和妥协解的概念[16].
不确定测度和不确定空间的概念已经众所周知,本节不再介绍它们。
定义1 如果ξ是从不确定空间(Γ,L,M)到实数集R的可测函数,即对任意Borel集{ξ∈B}={γ∈Γ|ξ(γ)∈B}是一个事件,则称ξ为(Γ,L,M)上的不确定变量.
定义2 设ξ是不确定空间(Γ,L,M)上的不确定变量.若对∀x∈R满足Φ(x)=M{ξ≤x}, 则称Φ是ξ的不确定分布.
定义3 如果不确定变量ξ的不确定分布Φ存在反函数Φ-1(α),α∈(0,1),则称不确定分布Φ是正规的,且称Φ-1(α)为ξ的逆不确定分布.
定义4 设ξ1,ξ2,…,ξm是不确定变量,如果对任意的Borel集B1,B2,…,Bm集B1,B2,…,Bm满足

则称ξ1,ξ2,…,ξm是相互独立的.
定义5 若ξ是不确定变量,则
为ξ的期望值,其中,两个积分中至少有一个是有限的.
定理1 设不确定变量ξ有不确定分布Φ,若其期望值存在,则
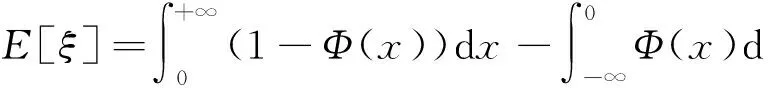
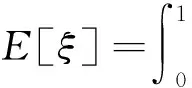
定理3 设ξ和η是存在有限的期望值并且相互独立的不确定变量,则对任意的实数a,b,我们都有E[aξ+bη]=aE[ξ]+bE[η].
定义6[16](多目标模型的有效解和妥协解)设模型
(a)
其中j=1,2,…,p,x=(x1,x2,…,xn)是一个n维决策向量,fi(x)(i=1,2,…,m)是目标函数,gi(x)(i=1,2,…,p)是系统的约束条件,S={x|gj(x)≤0,j=1,2,…,p}.一个x*∈S称为模型(a)有效解,如果不存在x∈S使得fi(x)≤fi(x*),=1=1,2,…,m.且不等号至少对一个序号j成立.
(b)
这里p1+p2+…+pm=1,j=1,2,…,p.模型(b)的解称为多目标的妥协解.
限于文章的篇幅,本文仅研究双目标的有效解,另文再研究其妥协解.
2 不确定单机排序的双目标模型
2.1 参数和变量的符号表示
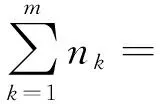
(ii)链k的第j个任务在该机器上的处理时间ξjk是一个具有正规分布Φjk的不确定变量,k=1,2,…,m,j=1,2,…,nk.
(iii)每两个相邻任务没有耽搁时间.
(iv)在每个时刻,机器仅能处理一个任务,且每个任务在机器上仅需要处理一次.



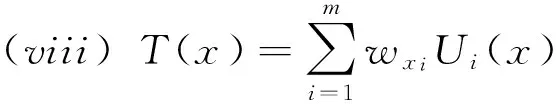
2.2 模型
基于(i)-(viii),我们提出下面的单机器排序的一个双目标不确定模型如下
(1)
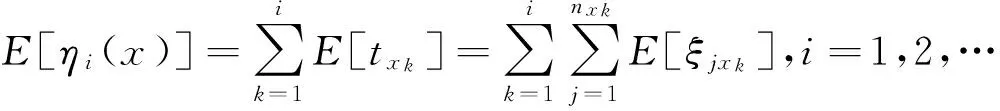
于是我们给出其对应的一个精确的数学模型如下
(2)
因为每个任务在该机器上的处理时间ξjk是一个具有正规分布Φjk的不确定变量,k=1,2,…,m,j=1,2,…,nk,所以根据定理2,模型(2)转化为如下形式:
(3)
3 模型的性质
为了求解模型(3),本节研究其性质. 首先引入下述概念.
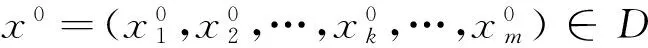
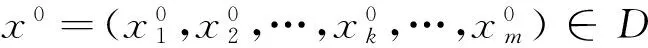

则(1)Ui(x1)=Ui(x0),i=1,2,…,k-1,k+p+1,…,m.(2)Ui(x1)≤Ui+1(x0),i=k,…,k+p-1.(3)Uk+p(x1)=Uk(x0)=1.
证明 (1)因为E[ηi(x1))=E[ηi(x0)),i=1,2,…,k-1,k+p+1,…,m,所以
Ui(x1)=Ui(x0),i=1,2,…,k-1,k+p+1,…,m.
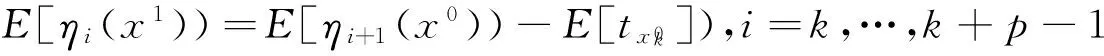
Ui(x1)≤Ui+1(x0),i=k,…,k+p-1.
(3)显然Uk+p(x1)=Uk(x0)=1.
由引理1易得下述引理.
引理2 在引理1的假设下,有T(x1)≤T(x0),即后移x0中真值为1的坐标可使模型(3)的第一个目标函数值不增.




证明 根据引理2有T(x1)≤T(x0).
因为l=max{i|Ui(x0)=0},所以根据引理1(1),有Ui(x1)=Ui(x0)=1,i>l+1.根据引理3(2),有Ul-1(x1)≤Ul(x0)=0. 故Ul-1(x1)=0.由引理1(3),Ul(x1)=1,所以

引理1-3说明模型(3)的有效解满足前边的任务对应的真值全为0,后边的任务对应的真值全为1,我们称这样的排序为0-1排序.


则它使得模型(3)的两个目标值不增.


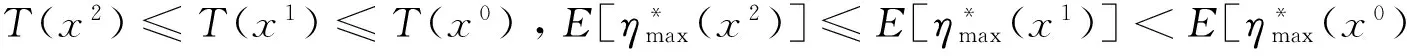

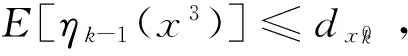
证明 (1)注意它是引理1的特别情况.
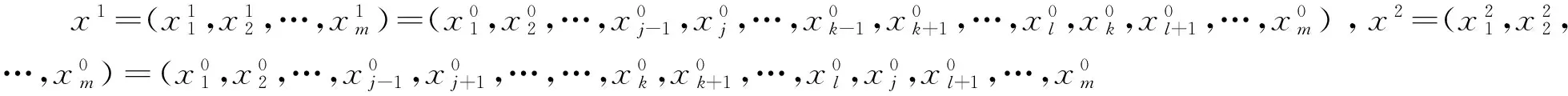
故E[ηi(x2)]=E[ηi(x1)]=E[ηi(x0)],i=1,2,…,j-1,l+1,…,m.已知Ui(x2)=Ui(x1)=Ui(x0)=0,i=1,2,…,j-1,Ui(x2)=Ui(x1)=Ui(x0)=1,i=l+1,…,m.
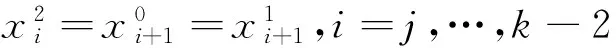

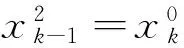

综上所述T(x1)=(0,0,…,0,Uk,…,Ul-2,0,1,1,…,1),T(x2)=(0,0,…,0,Uk,…,Ul-2,0,1,1,…,1).
这里x2,x1的前边k-1个0,后边m-(l-1)个1,第l-1个坐标是0.
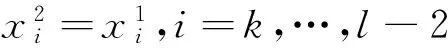
(3)该结论是显然的,证明略.

易见,定理4为我们提供了求模型(3)的有效解的方法.
5 结论
本文基于不确定理论,视任务的处理时间为不确定变量,提出了一个新的双目标整数规划模型. 引入了D-排序,1D-排序和0-1排序的概念,由此提供了该模型的性质.特别地,发现了该模型有一个0-1排序有效解,并提供了逼近模型有效解的方法.
[1]SmithWE.Variousoptimizersforsinglestageproduction[J].NavResLogistQ, 1956,3(1) 15:102-109.
[2]TangGC.Anewbranchandboundalgorithmforminimizingtheweightednumberoftardyjobs[J].AnnalsofOperationsResearch, 1990, 24:225-232.
[3]AgnetisA,PascaleG,PacciarelliD.ALagrangianapproachtosingle-machineschedulingproblemwithtwocompetingagents[J].JournalofScheduling, 2009,12: 401-415.
[4]WangD,GenM,ChengR.Schedulinggroupedjobsonsinglemachinewithgeneticalgorithm[J].Computers&industrialengineering, 1999,36 (2):309-324.
[5]LeeK,ChoiBC,LeungJYT,etal.Approximationalgorithmsformulti-agentschedulingtominimizetotalweightedcompletiontime[J].InformationProcessingLetters, 2009,109:913-917.
[6]G.Mosheiov(2001).Schedulingproblemswithalearningeffect[J].EuropeanJournalofOperationalResearch,2001,132:687-693.
[7] 李巧云,王冰,王晓明.随机机器故障下单机预测调度方法[J].系统工程理论与实践,2011,31(12):2 387-2 393.
[8]SeoDK,KleinCM,JangW.Singlemachinestochasticschedulingtominimizetheexpectednumberoftardyjobsusingmathematicalprogrammingmodels[J] .Computers&IndustrialEngineering, 2005,48(2):153-161.
[9]SaidiMehrabadM,PahlavaniA.Afuzzymulti-objectiveprogrammingforschedulingofweightedjobsonasinglemachine[J].TheInternationalJournalofAdvancedManufacturingTechnology,2009, 45(1-2): 122-139.
[10]LiuB.Uncertaintytheory[M]. 2nded,Springer-Verlag,Berlin,2007.
[11]LiuB.Uncertaintytheory:Abranchofmathematicsformodelinghumanuncertainty[M].Springer-Verlag,Berlin, 2010.
[12]LiuB.Someresearchproblemsinuncertaintytheory[J].JournalofUncertainSystems, 2009,3(1):33-10.
[13]GaoY.UncertainModelsforSingleFacilityLocationProblemsonNetworks[J].AppliedMathematicalModelling, 2012,36(6) : 2 592-2 599.
[14]ZhangX,LiX.ASemanticStudyoftheFirst-OrderPredicateLogicwithUncertaintyInvolved[J].FuzzyOptimDecisMaking, 2014,13: 357-367.
[15]ZhangX,NingY,MengG.Delayedrenewalprocesswithuncertaininterarrivaltimes[J].FuzzyOptimDecisMaking, 2013,12: 79-87.
[16]XuJ,ZhouX.Aclassofmulti-objectiveexpectedvaluedecision-makingmodelwithbirandomcoefficientsanditsapplicationtoflowshopschedulingproblem[J].InformationSciences, 2009, 179:2 997-3 017.
A New Model and Agorithm of Two Objectives for Uncertain Sngle Mchine Sheduling Problem
ZHANG Min1ZHANG Xing-fang2
(1.Grain Depot of Centra Preparations for the Food, Liaocheng 252000, China;2. School of Mathematical Sciences,Liaocheng University, Liaocheng 252059, China )
In the sngle machine scheduling problem, suppose that some jobs are divide into some groups( called chains). They have a due date and weight respectively. Processing time of job has uncertainty and no its historical data. Previous researches are concerned with how schedule a processing sequence of chains such that the total weighted number of tardy job is minimum or the total weighted completion time of chains is minimum or they is minimum simultaneously. In the paper , a new model of integral number of two objectives first is established based on uncertainty theory. Then, its properties are given.
sngle machine scheduling, the total weighted number of tardy jobs, completion time of final a job which can be finished before due date, uncertainty theory
2016-09-30
国家自然科学基金项目(11471152)资助
张兴芳,E-mail:zhangxingfang2005@126.com.
O29
A
1672-6634(2017)01-0027-06

