一类半线性椭圆型方程组边值问题的可解性
金启胜, 周宗福
(1.安庆师范大学,安庆职业技术学院,安徽 安庆 246003;2.安徽大学数学科学学院,安徽 合肥 230039)
一类半线性椭圆型方程组边值问题的可解性
金启胜1, 周宗福2
(1.安庆师范大学,安庆职业技术学院,安徽 安庆 246003;2.安徽大学数学科学学院,安徽 合肥 230039)
利用极大值原理和Holder,Poincare不等式,证明了一类半线性椭圆型方程组解的非负性和唯一性.在此基础上,又利用连续统理论证明了该边值问题有且仅有唯一的正解,推广了该边值问题可解性的结论.
连续统;紧正算子;极大值原理;正解
1 引言
考察一类半线性椭圆型方程组:

其中

λ>0为实参数.则问题 (2)存在起始于 (0,0),延拓出的解 (λ,U)的连续统
引理 1.1[1]设Z是一个Banach空间,T:R+×Z→Z是一个连续映射,则非线性特征值问题:

有一个相会于(0,0)∈R+×Z的解的无界连续统.引理1.1证明见参考文献[1].
引理1.2[2](极大值原理)设Z是一个Banach空间,正锥K⊂Z,:Z→Z是一个线性算子,所谓极大值原理就是对于问题U⊂U+H,U∈Z,在H≥0时,即H∈K时,能推出它的解U≥0.
引理1.3[2]设:Z→Z是一个线性紧正算子,若由条件{U∈Z,t∈[0,1],U=tU}能推出U=0,则问题U⊂U+H,U∈Z满足极大值原理.
引理1.2、引理1.3证明见参考文献[2].
2 主要结果及证明

该问题与问题(1)同解.
引进范数

λ1为Dirichlet条件下-∆在Ω里的第一特征值.
定理 2.1[3-4]如果|G(x)<λ1,那么问题(4)的解非负.

因为A(x)各项非负连续,所以L−1A(x)仍然是紧正算子.故问题(5)等价于:
将第k个方程两边乘以uk,k=1,2,···,n,并且在Ω上积分,利用格林公式可得

使用Holder不等式和Poincare不等式,可进一步得到:

把上面各式相加得到:

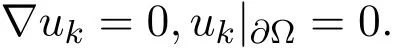
从而U≡0.又因为H(x)≥0,根据引理1.2和引理1.3可得到问题(4)的解U≥0.从而问题(1)的解非负.
定理 2.2如果问题(4)有解,那么其解必唯一.
证明不妨设U1,U2是问题(4)的两个解,则X=U1−U2满足方程:

这和问题(5)在t=1时等价.和定理1证明方法一样,可得到X=0.所以U1=U2.由问题(4)的解唯一可得到问题(1)的解也唯一.
定理 2.3[6]如果|G(x)|<λ1,那么问题(1)有一个正解.
证明设定义范数

则是一个Banach空间.根据定理2.1的证明可知,L−1:Z→Z是一个线性紧正算子.
在R+×Z里考虑方程:

因为L−1A,L−1H 为紧算子,由引理1.1可知,有一个相会于(0,0)∈R+×Z的解的无界连续统 W 存在.因为 hk(x),k=1,2,···,n中至少有一个大于零,所以如果有 (λ,0)∈W,那么 λ=0.显然 (U,0)∈W,所以 U=0.所以与R+×{0}|W相交于(0,0).如果λ≤1,根据定理2.1的证明可知,问题(10)的每一个解都是正的.因为W 无界,所以W可能.
分三种情况讨论:
(Ⅰ)W 关于λ无界;
(Ⅱ)W 关于U无界;
(Ⅲ)W 关于λ和U无界.
如果(Ⅰ)、(Ⅲ)成立,则 W 通过线{1}×Z,所以问题(4)有正解,从而问题(1)有正解.
设 (λ,U)∈W,λ ≤1,所以 W 关于 U 无界.存在一个序列 (λn,Un)∈W,满足
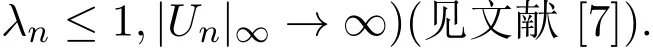
所以

所以V为问题(11)的非平凡解.而λ0≤1,根据定理2.1证明可知V≡0,显然矛盾.从而W通过线{1}×Z,问题(4)有一个正解,故问题(1)有一个正解.
参考文献
[1]Rabinowit P H.Some global results for nonlinear eigenvalue problems[J].Journal of Functtional Analysis,1971,7(4):487-513.
[2]Correa F J S A,Souto M A S.On maximum principle for cooperative elliptic systems Via fi xed point index.Nonlinear Analysis[J].Theory Methods and Application,1996,26(5):997-1006.
[3]辛奎东,黄国荣.一类(p,q)-Laplacian椭圆方程组解的存在性[J].纯粹数学与应用数学,2011,27(4):486-490.
[4]李华,马飞遥.含梯度项的椭圆方程组的边界爆破解[J].纯粹数学与应用数学,2016,32(4):640-648.
[5]Gilbarg D,Trudinger N S.Elliptic Partical Di ff erential Equations of Second Order[M].Berlin:Springer,1983.
[6]彭超权,王芳,刘颖.一类半线性椭圆型方程组非平凡解的存在性 [J].中南民族大学学报:自然科学版,2014,33(4):110-112.
[7]Deimling K.Nonlinear Functional Analysis[M].Berlin:Springer,1985.
Solvability of a class of semi-linear elliptic equations boundary value
Jin Qisheng,Zhou Zongfu
(1.Anqing Normal University,Anqing Vocational and Technical College,Anqing 246003,China;2.School of Mathematics Science,Anhui University,Hefei230039,China)
In this paper,we proved the non-negativity and uniqueness of the solution to a class of semilinear elliptic equations with the maximum principle and Holder and Poincare inequality.On the basis of this theory,we prove that the boundary-value problem has only one positive solution according to continuum theory,generalizing the conclusion of the solvability of boundary-value problem.
continuum,positive operator,maximum principle,positive solution
O175.2
A
1008-5513(2017)03-0248-06
10.3969/j.issn.1008-5513.2017.03.004
2017-01-21.
安徽省教育厅项目(2015jyxm539);安徽省自然科研项目(KJ2016A447).
金启胜(1972-),硕士,副教授,研究方向:主要从事微分方程研究.
2010 MSC:35J55

