伪补对称扩张Ockham代数
张雄盛,方捷
(广东技术师范学院数学与系统科学学院,广东 广州 510665)
伪补对称扩张Ockham代数
张雄盛,方捷
(广东技术师范学院数学与系统科学学院,广东 广州 510665)
研究peO代数类中的子类pe2,0K1,1,即满足恒等式 f3=f和 k2=idL的peO-代数.利用同余和代数的次直不可约,有如下的主要结果:如果L∈pe2,0K1,1,则L是真次直不可约当且仅当Con L≃{ω}⊕[G,Φ]⊕{ι}.这里 ω和 ι分别表示相等关系和泛关系,Φ表示由f(x)=f(y)确定的一个同余,G表示Glivenko同余.
p-代数;Ockham代数;扩张Ockham代数
1 引言
一个p-代数(或称伪补代数)是指一个具有最小元0的格L且赋予映射∗:L→L使得对任意 x∈L存在 x∗=max{y∈L|x∧y=0};等价地,x∧y=0⇔ y 6 x∗.一个 Ockham代数是一个有界分配格L并赋予对偶自同态f:L→L.在Ockham代数(L;f)中,K1,1-代数是它的一个重要的子类,其中f满足条件:f3=f.有关p-代数和Ockham代数的基本性质,见文献[1-2].
在文献 [3]中,作者介绍了 pO-代数.确切地来说,一个 pO-代数是代数 (L;f,∗),其中 (L;f)是 Ockham代数,(L;∗)是p-代数.同时,一元运算f和∗可相互交换.随后在2008年,文献[4]研究了扩张Ockham代数簇eO;即代数(L;f,k),其中L是有界分配格,f和k是 L的两个一元运算,使得 (L;f)是一个 Ockham代数,k是 (L;f)上的自同态.特别地,当k2=idL时,这样的代数(L;f,k)称之为对称扩张Ockham代数.他们在该文中特别刻画了对称扩张Ockham代数类中的一个子类e2,0M,即称为对称扩张de Morgan代数(L;f,k)的次直不可约性.这里的一元运算f和k满足条件:f2=idL和k2=idL.有关这些代数类的基本性质,见文献[2-4]或文献[6-8].
本文将考虑包含对称扩张Ockham代数和p-代数的一个代数类.定义如下:
一个伪补对称扩张K1,1代数,是指代数(L;f,k,∗).其中L是有界分配格,f,k和∗是L上的三个一元运算并且满足如下条件:
(1)(L;f,k)是一个扩张Ockham代数;
(2)(L;∗)是一个p-代数;
(3)f3=f且k2=idL;
(4)f,k和∗可相互交换.
我们将用pe2,0K1,1表示伪补对称扩张K1,1-代数类.
例 1.1[4]每个有限布尔格 (B;∧,∨,′,0,1)都可以被看作一个 pe2,0K1,1-代数.实际上,令A={a0,a1,···,an}为B的所有原子组成的集合,而且定义映射f:B→B使得

和映射k:B→B使得对于x∈B有k(x)=[f(x)]′.于是,如文献[4]例1.4所示,f2=idB和k2=idB.从而知,(L;f,k)是对称扩张de Morgan代数.显然,

例 1.2考虑下面所给出的代数L如图1,表1所示:

表1 代数L

图1 代数L
2 同余的性质
设(E;6)是一个有序集,a,b∈E.如果a?b同时b?a,则称a和b不可比较;否则称为可比较.我们将用a∥b表示a和b不可比较,用a∦b表示a和b可比较.
下面是文中所需要的引理:
引理 2.1(见文献[4,6]) 如果(L;f,k)是一个对称扩张Ockham代数,则
(1)(∀x∈L)x=k(x)或x∥k(x);
(2)对于x,y∈L并且x6y,如果x∧k(x)=y∧k(y)同时x∨k(x)=y∨k(y),则x=y.
引理 2.2(见文献 [2]) 如果 (L;∗)是一个p-代数,则

定理 2.1如果L∈pe2,0K1,1,则下面论断成立:

证明(1)如果 x ∈ L 则 x 6 x∗∗,所以 f(x)>f(x∗∗)=[f(x)]∗∗>f(x),由此可得 f(x∗∗)=f(x).
(2)令x∈L,由(1)可得

由此推知,(f(L);∗)是布尔代数.类似地,(fk(L);∗)也是布尔代数.
为了术语上的便利,将 f(x)记为 x◦,k(x)记为 x+并且将 pe2,0K1,1-代数 (L;f,k,∗)记为 (L;◦,+,∗).同样,将 f(L)记为 L◦={x◦|x∈L}和 fk(L)记为 L◦+={x◦+|x∈ L}.
pe2,0K1,1-代数(L;◦,+,∗)上的一个同余,是指一个格同余 ϑ使得

设 (L;◦,+,∗)是一个 pe2,0K1,1-代数.用 ConL表示 L的同余格;用 ConlatL表示格 L的格同余格.用符号 ω和 ι分别表示 L的相等关系和泛关系.正如文献 [1,6]所见,Glivenko同余 G,给出由 (x,y)∈ G ⇔ x∗=y∗,是 p-代数 (L;∗)的一个同余.同时,由(x,y)∈Φ⇔f(x)=f(y)给出的关系Φ是K1,1-代数的一个同余.我们有如下的定理:
定理 2.2设 (L;◦,+,∗)∈pe2,0K1,1.则 G 和 Φ 都是 L的同余并且 G 6 Φ.
证明如文献 [6],G是一个 ∗-同余.为证 G也是一个 (◦,+)-同余,令 (x,y)∈G则有 x∗=y∗.故有

从而推知

因此,G是(◦,+)-同余,从而它是L的一个同余.类似可证,Φ也是L的同余.
最后,设 (x,y)∈G.则 x∗=y∗.由定理 2.1,有

因此,(x,y)∈Φ.从而得到 G 6 Φ.
定理 2.3设 (L;◦,+,∗)∈pe2,0K1,1.则下列论断成立:
(1)G=ω⇔ (L;∗)是布尔代数;
(2)Φ = ω ⇔ (∀x ∈ L)x∗∗=x◦◦=x;
(3)Φ =G ⇔ (∀x ∈ L)x∗∗=x◦◦.
证明(1)如果 G=ω,则对任意 x∈L,有 (x∨x∗,1)∈G=ω.于是得 x∨x∗=1.因此(L;∗)是布尔代数.反过来显然成立.
(2)如果 Φ= ω,则由定理 2.2知,G=ω.因此由 (1),对任意 x∈L,有 x∗∗=x.由于 (x,x◦◦)∈Φ=ω,于是有x◦◦=x.故结论成立.反过来显然成立.
(3)如果 Φ=G,则对 x∈L,由于 (x,x◦◦)∈ Φ=G,因此有
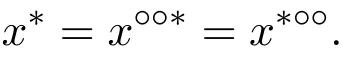
故由定理2.1(1)知,
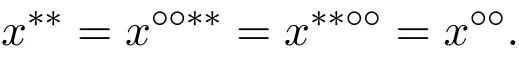
反之,对于任意x∈L,如果

则

现若 (x,y)∈ Φ 则 x◦=y◦,由此推知

故(x,y)∈G.从而有Φ 6 G.因此由定理2.2推知,Φ=G.
给定a,b∈L并且a 6 b,用θ(a,b)表示关于a和b的主同余;即由a和b生成的(L;◦,+,∗)上的最小同余;用θlat(a,b)表示相应地格L上的主格同余;用θ∗(a,b)表示(L;∗)的主∗-同余;用 θ◦(a,b)表示 (L;◦)的主 ◦-同余.正如文献 [1,6]中所述,有

下面给出pe2,0K1,1-代数的主同余表示:
定理 2.4若 (L;◦,+,∗)∈pe2,0K1,1及 a,b∈L 并且 a 6 b,则

证明令 φ(a,b)为 (†)中右边的第一个等式.显然有 φ(a,b)6 θ(a,b).如文献 [6]的 41页 (3)和定理 5.9 中所见,θ◦(a,b)∨ θ◦(a+,b+)是 (◦,+)-同余,θ∗(a,b)和 θ∗(a+,b+)是 ∗-同余.因此为证 φ(a,b)是一个同余,只需证明 θ◦(a,b)∨θ◦(a+,b+)是 ∗-同余同时 θ∗(a,b)∨θ∗(a+,b+)是 (◦,+)-同余.为此,只需观察如下事实:

则

后者给出 x∗∧q◦∗=y∗∧q◦∗,从而由定理 2.1 推知 x∗∨q◦=y∗∨q◦.前者给出

因此得到 (x∗,y∗) ∈ θlat(p◦,q◦).

则

从而推知

因此得到 (x∗,y∗)∈ θlat((a∗∧ b)∗+,1).
类似地,如果

于是有

因此由定理2.1可得

再由定理2.1,有

从而得到

综上所述,可推知φ(a,b)是一个同余.故θ(a,b)6 φ(a,b).显然,有

和

故 φ(a,b)6 θ(a,b).因此等式成立.
推论 2.1设L∈pe2,0K1,1.如果a,b∈L◦使得a 6 b,则

证明因为 (L◦;∗)是布尔代数,所以有

注意到 a∗∗=a 和 b∗∗=b,于是有
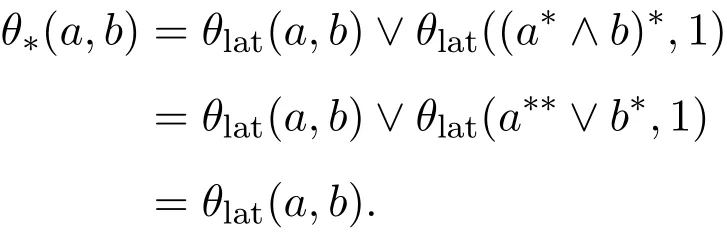
类似地,可证 θ∗(a+,b+)=θlat(a+,b+).因此由定理 2.4,等式 (‡)成立.
推论 2.2设L∈pe2,0K1,1.如果a,b∈L并且a 6 b使得(a,b)∈G,则

证明设 (a,b)∈G 并且 a 6 b,则 a∗=b∗.因 G 6 Φ,故 a◦=b◦.从而由定理 2.4,等式成立.
3 次直不可约性
本节中,我们将考虑次直不可约pe2,0K1,1-代数.我们说一个代数L是次直不可约,如果存在L的一个同余α使得对于所有θ∈ConL且θ≠ω,都有α>θ.这样的一个同余α被称为L的唯独元.余唯独元可对偶地定义.一个次直不可约代数是单纯的,如果其同余格ConL是一个2-元素链ω<ι,即ConL={ω,ι}.称一个次直不可约代数是真次直不可约,如果它不是单纯的.
设Fix+(L)={x∈L|x+=x}.
定理 3.1设L∈pe2,0K1,1.若L是次直不可约,则有
(1)ω≼G;
(2)(∀x∈L)|[x]G∩Fix+(L)|6 2;
(3)(∀x∈L)|[x]G|6 4.确切地说,[x]G是一个单元素集,或是以下两种形状中的一种,如图 2,图3所示:

图2

图3
证明(1)假设G̸=ω.因L是次直不可约的,故存在L的一个唯独元α使得

因而有a,b∈L且a 不妨假定a∧a+̸=b∧b+,则 因此由推论2.2推知 令 则在ConlatL中,有 不难看出,β∧G是L的同余.从而得 后面一种情况是不可能的,因为它给出α=α∧β∧G=α∧β=ω,一个矛盾.因此必有β∧G=ω.于是得 故G是L的唯独元. (2)用反证法.假设存在一个 [x]G,它至少包含 Fix+(L)中的三个元素,即a,b,c∈L且a 则由定理2.4,有 这与L的次直不可约性相矛盾.因此必有|[x]G∩Fix+(L)|6 2. (3)假若存在xi∈L(i=1,2,3,4)使得 则有 以及 由 (2),存在某个i∈{1,2,3}使得 从而由引理 2.1推知,xi=xi+1,这与假设矛盾.因此必有|[x]G|6 4.再由(2),得到所要求的Hasse图. 记 定理 3.2设L∈pe2,0K1,1是次直不可约.则有 证明设 则 故由定理2.1知x∗和x是互补元.如果x/∈Fix◦(L) 则 由推论 2.1,有 由L的次直不可约性推知, 故 x∧x◦=0,因而 又由L的分配性,得x◦=x∗.再由推论2.1,有 由此知 因而有x∈{0,1},从而得 相反的包含关系是显然的.题设的等式成立. 定理 3.3若L∈pe2,0K1,1是次直不可约,则S(L)是单纯代数. 证明只需证明,对任意x,y∈S(L)及x 假设 则 由引理 2.1,有 不妨假定x∧x+ 或者 或者 这三种情况都蕴含着 θ(x∧x+,y∧y+)=ι,由此推知 θ(x,y)=ι.结论对 x∨x+≠y∨y+的情况同样成立.因此,S(L)是单纯的. 推论 3.1若L∈pe2,0K1,1是次直不可约,则Φ是L的余唯独元. 证明因为L/Φ≃S(L),所以有 由定理 3.3可知,区间 [Φ,ι]是一个 2-元素链.故结论成立. 设A和B是两个不相交的有序集.将用A⊕B表示由A∪B生成的线性和,其序关系由下面所给出: 定理 3.4设L∈pe2,0K1,1.则L是真次直不可约当且仅当ConL≃{ω}⊕[G,Φ]⊕{ι}. 证明(⇒:)设L是真次直不可约,则由推论 3.1有 Φ≺ι,同时由定理2.3和定理3.1,Φ≠ω.由后者,存在L的一个唯独元α使得ω≺α 6 Φ.有x,y∈L且x 如果G=ω,则由定理2.3知(L;∗)是布尔代数,因而有 故 类似于定理3.1(1)中的证明,可得 从而有 另一方面,若G≠ω,则由定理3.1和定理3.3,结论成立. (⇐:)这是显然的. 例 3.1例1.2中所描述的两个pe2,0K1,1-代数(L;f1,+,∗)和(L;f2,+,∗),它们都是次直不可约.其中(L;f1,+,∗)的同余格是一个3-元素链:ω≺G=Φ≺ι,这里G=Φ=θ(a,d);(L;f2,+,∗)的同余格是一个4-元素链:ω≺G≺Φ≺ι,这里G=θ(a,d)和Φ=θ(0,d). 例 3.2考虑由下面的Hasse图所确定的pe2,0K1,1-代数(L;◦,+,∗),如图4,表2所示: 图 4 pe2,0K1,1-代数 表 2 pe2,0K1,1-代数 显然,L是次直不可约的且ConL诱导出一个3-元素链:ω=G≺Φ≺ι,其中Φ=θ(0,c). 例 3.3考虑由下面 Hasse图所确定的 pe2,0K1,1-代数 (L;◦,+,∗),如图 5,表 3所示: 图 5 pe2,0K1,1-代数 表 3 pe2,0K1,1-代数 可以看出,L的同余格ConL具有如下形式,如图6所示: 图6 L的同余格 [1]Blyth T S,Varlet J C.Ockham Algebras[M].Oxford:Oxford University Press,1994. [2]Fang Jie.Distributive Lattices with Unary Operations[M].Beijing:Science Press,2011. [3]Blyth T S,Fang Jie,Varlet J C.Ockham algebras with pseudocomplementation[J].Communications in Algebra,1997,25(11):3605-3615. [4]Blyth T S,Fang Jie.Extended Ockham algebras[J].Communications in Algebra,2008,25:1271-1284. [5]Fang Jie.Pseudocomplemented MS-algebras[J].Algebra Colloquium,1996,3(1):59-65. [6]Blyth T S,Fang Jie.Symmetric extended Ockham algebras[J].Algebra Colloquium,2003,10(4):479-489. [7]Berman J.Distributive lattices with an additional unary operation[J].Aequationes Math.,1977,16:165-171. [8]Gratzer G,Lakser H.The structure of pseudo-complemented distributive latticeⅡ,Congruence extension and amalgamation[J].Trans.Amer.Math.Soc.,1971,156:343-358. Pseudocomplemented symmetric extended Ockham algebras Zhang Xiongsheng,Fang Jie In this paper,we particularly study of the peO algebras that belong to the subclass pe2,0K1,1,characterised by the identities f3=f and k2=idL.By using properties of congruences on such an algebra and the subdirectly irreducibility,the main result obtained in this paper is if L∈pe2,0K1,1,then L is properly subdirectly irreducible if and only if ConL ≃ {ω} ⊕ [G,Φ]⊕ {ι},where ω and ι stand for the equality relation and the universal relation respectively,Φ denotes the relation determined by f(x)=f(y)and G denotes the Glivenko relation. p-algebra,Ockham algebra,extended Ockham algebra O153.1;O153.2 A 1008-5513(2017)03-0314-12 10.3969/j.issn.1008-5513.2017.03.011 2016-11-03. 张雄盛(1991-),硕士生,研究方向:格论与序代数 2010 MSC:06B10,06D15,06D30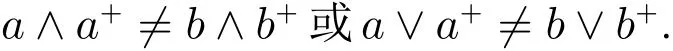








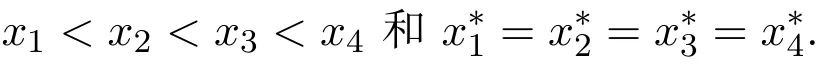















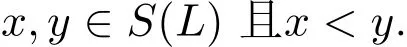

















(School of Mathematics and System Science,Guangdong Polytechnic Normal University,guangzhou 510665,China)

