广义(3+1)维Zakharov-K uznetsov方程的对称约化、精确解和守恒律∗

张丽香 刘汉泽 辛祥鹏

(聊城大学数学科学学院,聊城252059)

广义(3+1)维Zakharov-K uznetsov方程的对称约化、精确解和守恒律∗

张丽香 刘汉泽†辛祥鹏

(聊城大学数学科学学院,聊城252059)

(2016年1月1日收到;2017年1月2日收到修改稿)

运用李群分析,得到了广义(3+1)维Zakharov-Kuznetsov(ZK)方程的对称及约化方程,结合齐次平衡原理,试探函数法和指数函数法得到了该方程的群不变解和新精确解,包括冲击波解、孤立波解等.进一步给出了广义(3+1)维ZK方程的伴随方程和守恒律.

Zakharov-Kuznetsov方程,李群分析,精确解,守恒律

1 引言

非线性发展方程的求解一直是数学和物理工作者研究的热点问题,经过多年研究,提出了许多有效的方法,如经典李群方法[1−3],改进的tanh函数方法[4],Hirota方法[5],Painlevé截断展开法[6],Clarkson-K ruskal直接约化方法[7,8],(G′/G)展开方法[9],Jacobi椭圆函数展开法[10].其中李群方法是研究偏微分方程的有力工具之一,本文将采用李群分析研究广义(3+1)维Zakharov-Kuznetsov(ZK)方程

其中u=u(x,y,z,t),a1,a2,a3,a4,a5,a6是任意非零常数.方程(1)包含了许多著名的方程,例如当a1=a3=a4=a6=0时,该方程就是著名的Korteweg-de Vries方程[11];当a1=a2=a3=a4=0时,该方程就是正则长波方程[12];当a2=a4=a5=0时,该方程就是(2+1)维ZK-MEW方程[13,14];当a1=a4=a6=0时,该方程就是(2+1)维ZK方程[15];当a2=a3=a4=a5=0时,该方程就是修正的(1+1)维MEW方程.

本文主要由以下几部分组成:第2部分,求出方程(1)的李点对称;第3部分,对方程(1)进行约化;第4部分,利用试探函数法[16]、指数函数法[17]和齐次平衡原理[18−20],求约化方程的精确解,进而得到方程(1)的精确解;第5部分,给出方程(1)的伴随方程和守恒律[21−24];最后,对本文做简要总结.

2 广义(3+1)维ZK方程的对称

设方程(1)的单参数向量场为

其中,ξ1(x,y,z,t,u),ξ2(x,y,z,t,u),ξ3(x,y,z,t,u),ξ4(x,y,z,t,u),ϕ(x,y,z,t,u)是待定函数.若向量场(2)是方程(1)的李点对称,那么V需要满足以下李对称条件:

其中pr(3)V是V的三阶延拓,并且∆=ut+a1u2ux+a2uxxx+a3uxyy+a4uxzz+a5uux+a6uxxt.

必须且只需

其中,系数函数

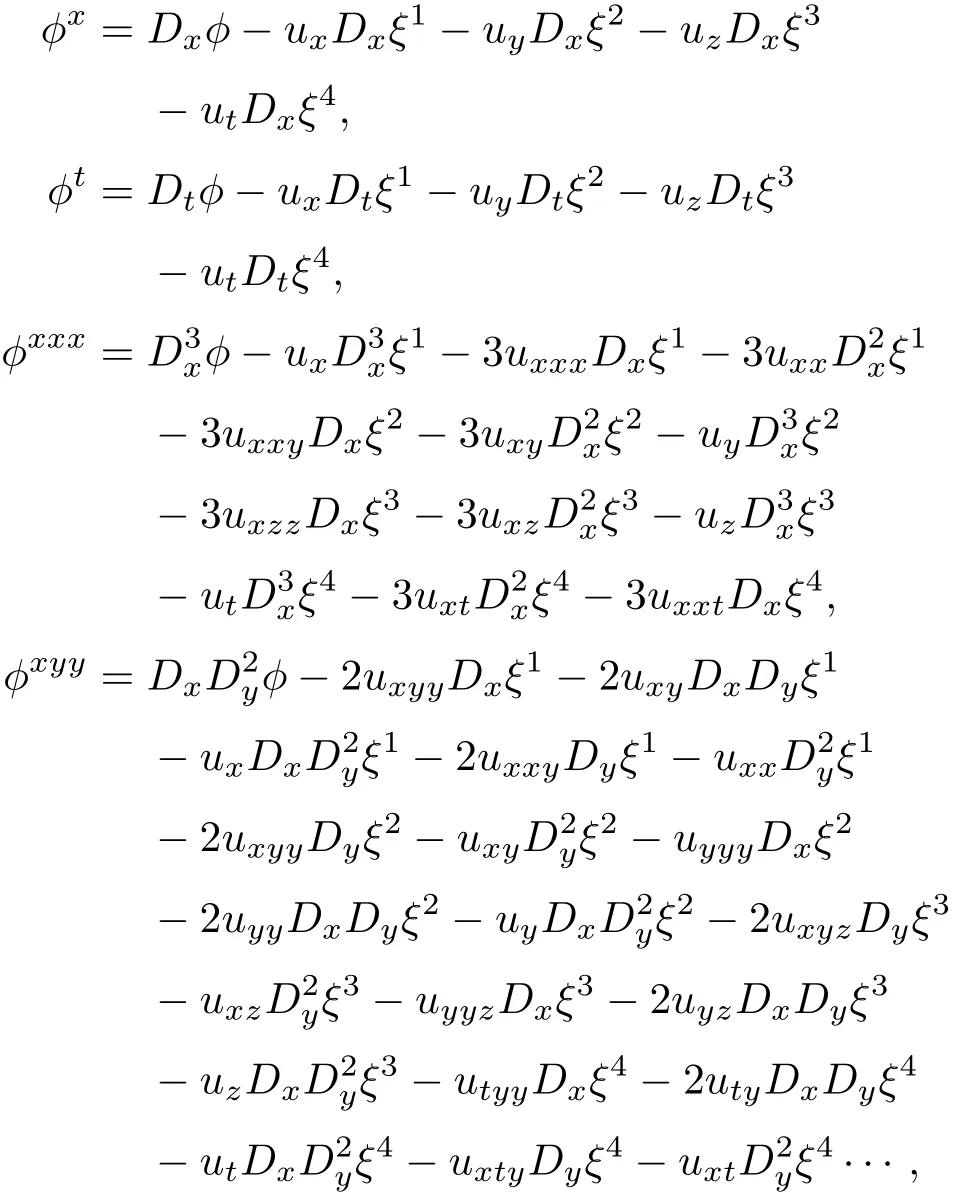
其中Dx,Dy,Dz,Dt为全导算子.把以上系数函数代入(5)式,得到关于ξ1,ξ2,ξ3,ξ4,ϕ的决定方程组,解之得

其中C1,C2,C3,C4,C5为任意常数.同时也得到了方程(1)的相似对称

这样就利用李群分析得到了方程(1)的所有向量场

与它们相对应的单参数变换群为

根据上面的单参数不变群可知,若u=f(x,y,z,t)是方程(1)的解,下列u1,u2,u3,u4,u5也是方程(1)的解:

其中ε是任意常数.

3 广义(3+1)维ZK方程的对称约化

可以得到下面的相似变换

在前面,已经得到了方程(1)的对称,在这部分,对方程(1)进行约化.

情况1令C2=1,C1=C3=C4=C5=0,则

方程(1)的群不变解为w=f(ξ,η),即u=f(ξ,η),代入方程(1)中,可将方程(1)约化成(1+1)维偏微分方程

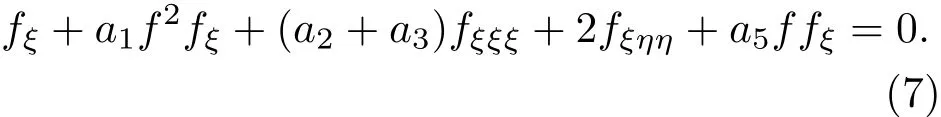
情况2令C2=C4=0,C1=C3=C5=1,则

可以得到下面的相似变换

方程(1)的群不变解为u=f(ξ),代入方程(1)中,得约化后的常微分方程为

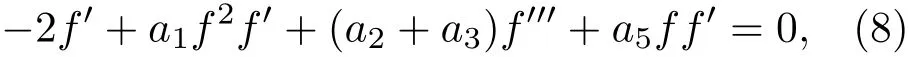
其中f′=d f/dξ.

情况3令C1=1,C2=C3=C4=C5=0,则

可以得到下面的相似变换

方程(1)的群不变解为u=f(ξ),代入方程(1),可得到约化后的常微分方程为

其中f′=d f/dξ.

情况4令C1=C2=0,C3=C4=C5=1,则

可以得到下面的相似变换

方程(1)的群不变解为u=f(ξ),代入方程(1),可得到约化后的常微分方程为

其中f′=d f/dξ.约化后的方程(10)和方程(9)相同.

4 广义(3+1)维ZK方程的精确解

在这一部分,结合齐次平衡原理、指数函数法和试探函数法,对约化后的方程(7)—方程(9)分别求其精确解,进而得到方程(1)的精确解.

情况1为求方程(7)的解,我们应用齐次平衡原理,假设方程(7)有如下形式的解

其中g=g(h),h=h(ξ,η).由齐次平衡原理,得到m=1,n=0,故方程(7)有如下形式的解

将(11)代入方程(7)中,合并h的各种偏导数同次项,并令的系数为零,得到

把以上等量关系代入(11)式,得

解(12)式—(14)式得

把上式代入(12)式—(14)式得

故方程(7)的准确孤立波解为

因此,方程(1)的精确解为

情况2为求方程(8)的解,我们利用试探函数法求其冲击波解.对方程(8)积分一次得

其中

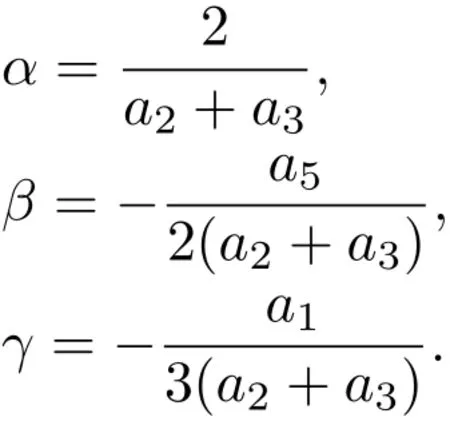
假设方程(15)有如下形式的解:

因此,方程(1)的解为

情况3为求方程(9)的解,我们结合指数函数法和齐次平衡原理求其精确解.为方便,把方程(9)写成以下形式:

假设方程(17)有如下形式的解:

其中c,d,p,q为正整数,cn,bm为待定常数.则

其中di为各项系数.平衡最高阶导数项(19)式和非线性项(20)式的次数,得

同理,平衡最低阶导数项和非线性项次数得q=d,为计算简便,令p=c=1,且q=d=1,故(18)式为

把(21)式代入方程(17)中,借助Maple软件,得到关于eiξ的各项系数,令每项系数为零,可以得到关于c−1,c0,c1,b0,b−1的超定方程组,解得

其中

c1,b0为任意常数,故方程(17)的解为

因此,方程(1)的解为

其中

c1,b0为任意常数.

5 广义(3+1)维ZK方程的伴随方程和守恒律

在这部分,我们将给出方程(1)的伴随方程和守恒律.方程(1)的伴随方程为

并且Largrangian记作

利用Ibragimov的结论,守恒向量的公式为

根据Ibragimov给出的结论,我们给出向量场的通式:

那么方程(1)的守恒律由下式决定:

则向量场C=(C1,C2,C3,C4)由下面的式子决定:

以上守恒向量(C1,C2,C3,C4)包含了伴随方程(21)的任意解,因此以上守恒向量给出了方程(1)的无穷多个守恒律.

6 结论

本文利用李群分析求得了广义(3+1)维ZK方程的李点对称,将(3+1)维方程直接约化成常微分方程和(1+1)维偏微分方程,并结合齐次平衡原理,试探函数法和指数函数法对约化方程求其精确解,从而得到原方程的精确解.丰富了广义(3+1)维ZK方程的显示解.可见,李群分析对偏微分方程的求解问题有重要的作用,李群分析在其他领域的应用,有待进一步研究.

[1]O lver P J 1993 Applications of Lie Groups to D iff erential Equations(New York:Sp ringer)pp186–206

[2]T ian C 2001 Applications of Lie Groups to D iff eren tia l Equations(Beijing:Science Press)pp243–248(in Chinese)[田畴2001李群及其在微分方程中的应用(北京:科学出版社)第243—248页]

[3]Cao L M,Si X H,Zheng L C 2016 J.App l.Math.Mech.37 433

[4]Li D S,Zhang H Q 2005 Acta Phys.Sin.54 1569(in Chinese)[李德生,张鸿庆2005物理学报54 1569]

[5]H irota R,SatsuMa J 1976 Suppl.Prog.Theor.Phys.59 64

[6]W eiss J,Tabor M,Carnevale G 1983 J.Math.Phys.24 522

[7]C larkson P 1989 J.Math.Phys.30 2201

[8]Lou S Y,Ma H C 2005 J.Phys.A:Math.Gen.38 L129

[9]W ang ML,Li X Z,Zhang J L 2008 Phys.Lett.A 372 417

[10]Pan J T,Gong L X 2007 Acta Phys.Sin.56 5585(in Chinese)[潘军廷,龚伦训2007物理学报56 5585]

[11]Pang J,Bian C Q,Chao L 2010 App l.Math.Mech.30 884(in Chinese)[庞晶,边春泉,朝鲁2010应用数学和力学30 884]

[12]Naher H,Abdullah F A 2014 Res.J.Appl.Sci.Eng.Techno l.7 4864

[13]Han Z,Zhang Y F,Zhao Z L 2013 ComMun.Theor.Phys.60 699

[14]Xu F,Yan W,Chen Y L 2009 CoMput.Math.Appl.58 2307

[15]W azwaz A M2005 ComMun.Non linear Sci.NuMer.SiMu l.10 97

[16]Liu S S,Fu Z T,Liu S D,Zhao Q 2001 App l.Math.Mech.22 281(in Chinese)[刘式适,付遵涛,刘式达,赵强2001应用数学和力学22 281]

[17]He J H,W u X H 2006 Chaos,Solitions and Fractals 30 700

[18]Zhang H Q 2001 J.Math.Phys.21A 321(in Chinese)[张辉群2001数学物理学报21A 321]

[19]W ang ML,Zhou Y Z,Li Z B 1996 Phys.Lett.A 216 67

[20]W ang ML,Li Z B,Zhou Y B 1999 J.Lanzhou Univ.35 8(in Chinese)[王明亮,李志斌,周宇斌1999兰州大学学报35 8]

[21]Ib ragiMov Z H 2006 J.Math.Anal.Appl.318 742

[22]Ib ragiMov Z H 2007 J.Math.Anal.Appl.333 311

[23]X i X P,Chen Y 2013 ComMun.Theor.Phys.59 573

[24]Li K H,Liu H Z,X in X P 2016 Acta Phys.Sin.65 140201(in Chinese)[李凯辉,刘汉泽,辛祥鹏2016物理学报65 140201]

(Received 1 January 2016;revised Manuscrip t received 2 January 2017)

PACS:02.20.–a,04.20.Jb,02.30.Jr,11.30.–jDOI:10.7498/aps.66.080201

*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.11171041,11505090).

†Corresponding author.E-Mail:hnz_liu@aliyun.com

SymMetry reductions,exact equations and the conservation law s of the generalized(3+1)d iMensional Zakharov-K uznetsov equation∗

Zhang Li-Xiang Liu Han-Ze†Xin Xiang-Peng

(School ofMatheMatical Sciences,Liaocheng University,Liaocheng 252059,China)

Because the nonlinear evolution equations can describe the coMp lex phenomena of physical,cheMical and biological field,Many Methods have been p roposed for investigating such types of equations,and the Lie symMetry analysis Method is one of the powerful tools for studying the non linear evolution equations.By using the Lie symMetry analysis method,we can obtain the symmetries,reduced equations,group invariant solutions,conservation laws,etc.In the reduction process,we can reduce the order and diMension of the equations,and a coMp lex partial diff erential equations(PDE)can be reduced to ordinary diff erential equations directly,which siMp lifies the solving p rocess.Meanwhile,the symmetries,conservation laws and exact solutions to the nonlinear partial diff erential equations p lay a significant role in non linear science and MatheMatical physics.For exaMp le,we can obtain a lot of new exact solutions by the known symMetries of the original equation;through the analysis of the special forMof solution we can better exp lain soMe physical phenomena.In addition,the studying of conservation laws and symmetry groups is also the central topic of physical sciencein both classicalMechanics and quantuMMechanics.Lie symMetry analysisMethod is suitab le for not on ly constant coeffi cient equations,but also variab le coeffi cient equations and PDE systeMs.By using Lie symmetry analysismethod,the symmetriesand corresponding symmetry reductionsof the(3+1)dimensionalgeneralized Zakharov-Kuzetsov(ZK)equation are obtained.Combining the hoMogeneous balance princip le,the trial function Method and exponential functionmethod,the group invariant solutions and some new exact exp licit solutions are obtained,including the shock wave solutions,solitary wave solutions,etc.Then,we give the conservation law s of the generalized(3+1)diMensional ZK equation in terMs of the Lagrangian and ad joint equation Method.

Zakharov-Kuznetsov equation,Lie symmetry analysis,exact solution,conservation law

10.7498/aps.66.080201

∗国家自然科学基金(批准号:11171041,11505090)资助的课题.

†通信作者.E-Mail:hnz_liu@aliyun.com

©2017中国物理学会C h inese P hysica l Society

http://w u lixb.iphy.ac.cn