弱奇异迭代积分不等式中未知函数的估计
黄春妙, 王五生
(河池学院数学与统计学院,宜州 546300)
弱奇异迭代积分不等式中未知函数的估计
黄春妙, 王五生*
(河池学院数学与统计学院,宜州 546300)
给出了一类积分项外包含非常数项的非线性弱奇异迭代积分不等式,并利用离散Jensen不等式、Hölder积分不等式、变量替换技巧和放大技巧等分析手段给出了该非线性弱奇异迭代积分不等式中未知函数的上界估计,最后举例说明所得估计可以用来研究分数阶积分方程解的定性性质.
弱奇异三重积分不等式; 离散Jensen不等式;Hölder积分不等式; 分析技巧; 显式上界估计
Gronwall积分不等式[1]是最著名的积分不等式,表述为:

其中:u和f是区间[a,b]上的非负连续函数,c≥0是常数,未知函数u(t)有估计式
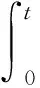
(1)
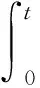
ABDELDAIM和YAKOUT[13]研究了 Gronwall-Bellman-Pachpatte 型积分不等式
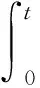
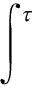
(2)
本文受文献[11]和文献[13]的启发,给出了下面的弱奇异迭代积分不等式:
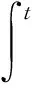
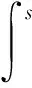
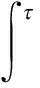
(t[0,+)),
(3)
把式(1)、(2)分别推广成迭代奇异积分不等式、奇异不等式;利用离散 Jensen 不等式、Cauchy-Schwarz积分不等式、变量替换技巧和放大技巧等分析手段,给出了式(3)中未知函数u(t)的上界估计.
1 预备知识
为了研究式(3),我们需要下面的引理.
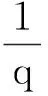
(4)
引理2[11]如果β(0,1/2],p=1+β,则

(t0+),
(5)
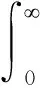
引理3[14](离散 Jensen不等式)令A1,A2,…,An,l>1表示非负实数,n表示自然数,那么
(6)
2 主要结果与证明
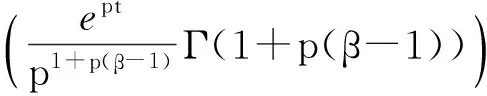
(7)

(8)

(9)

(10)
其中c为正常数.
定理1 假设β(0,1/2)是常数,函数fi,bC([a,),+)(i=1,2,3),b是正的不减函数. 假设函数φiC(+,+)(i=1,2,3)是正的不减函数,而且φ1(z)/φ3(z),φ2(z)/φ3(z),φ2(z)/φ1(z)也都是正的不减函数. 如果未知的非负连续函数u(t)满足式(3),则函数u(t)的估计为u(t)≤{{[(Ξ(t))]}}1/q(t[a,T1]),
(11)
其中:
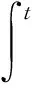

(12)
T1是满足下面条件的最大实数:
Ξ(T1)≤Φ3(),
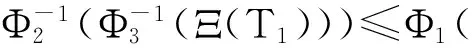
(13)
证明 利用式(4)和式(5),由式(3)推出
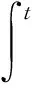
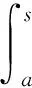
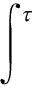
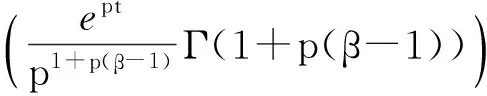
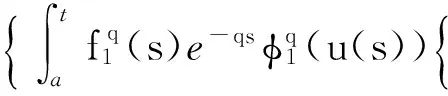
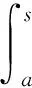
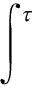
(14)
uq(t)≤2q-1bq(t)+2q-1P(t)×
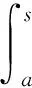
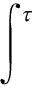
(t[a,T1]).
(15)
利用式(6)、(4)和式(5),对任意t[a,T1],有
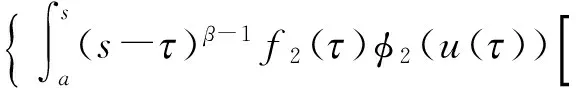
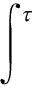
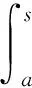
2q-1P(.
(16)
uq(t)≤2q-1bq(T)+2q-1P(T)×
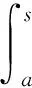
2q-1P(
(t[a,T]).
(17)
用z1(t)表示式(17)的右端. 显然,z1(t)是区间[a,T]上正的不减函数,并且有
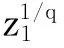
(18)
求函数z1(t)的导函数,利用式(18),得到
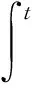
2q-1P(
(t[a,T]),
(19)
其中z2(t)定义如下:
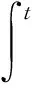
(20)
可以看出z2(t)是[a,T]上正的不减函数. 由式(18)和式(20)知
z1(t)≤z2(t) (t[a,T]),z2(a)=2q-1bq(T).
(21)
求函数z2(t)的导函数,利用式(19)和式(21)得:对任意t[a,T],有
(22)
其中z3(t)定义如下:
(t[a,T]).
(23)
显然,z3(t)是[a,T]上正的不减函数. 由式(21)和式(23)知
z2(t)≤z3(t) (t[a,T]),z3(a)=2q-1bq(T).
(24)
求函数z3(t)的导函数,利用式(22)和式(24),得到
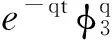
(25)
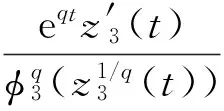
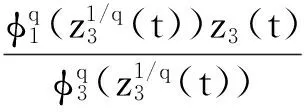
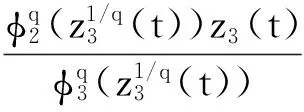
(26)
先把式(26)中的t替换成,然后两边从a到t进行积分,得到

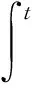
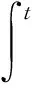
(t[a,T]).
(27)
用z4(t)表示式(27)的右端,则z4(t)是[a,T]上正的不减函数,且
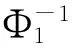
(28)

(29)
类似于对式(25)、(26)的推导,可得函数z4(t)的导函数,利用式(28)可以进一步得到:对任意t[a,T],有Φ2(z4(t))≤Φ2(z4(a))+a4q-1P(T)fq1(s)ds+
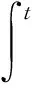
(30)
用z5(t)表示式(30)的右端,则z5是[a,T]上正的不减函数,且
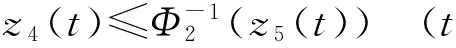
(31)
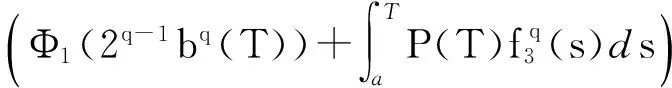

(32)
类似于对式(27)的推导,由式(30)和式(31)推出
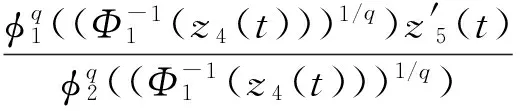
(33)
由式(33)进一步推出

(34)
综合式(18)、(21)、(24)、(28)和式(31),推出
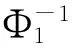
(35)
把式(32)、(34)代入式(35),推出


(36)
令式(36)中的t=T,得到


(37)
由于T[0,T1]的任意性,得到估计(11).
3 应用
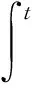
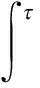
(38)
其中k是常数. 假设F1,F2C([a,)×2,),F3C([a,)×,)满足下面的条件:
|F1(t,x,y)|≤f(t)φ1(|x|)[|x|+|y|],
(39)
|F2(t,x,y)|≤g(t)φ2(|x|)[|x|+|y|],
(40)
|F3(t,x)|≤h(t)φ3(|x|),
(41)
其中函数f,g,h,φi(i=1,2,3)满足定理1的条件.
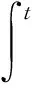
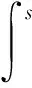
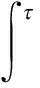
(42)
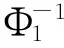
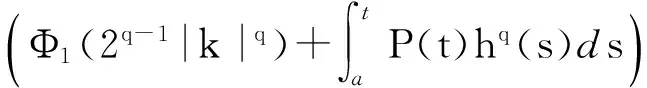

Φi(i=1,2,3)、T1的定义与定理1的定义相同,
[1] GRONWALL T H. Note on the derivatives with respect to a parameter of the solutions of a system of differential equations[J]. Annals of Mathematics,1919,20:292-296.
[2] AGARWAL R P,DENG S,ZHANG W. Generalization of a retarded Gronwall-like inequality and its applications[J]. Applied Mathematics and Computation,2005,165:599-612.
[3] 黄裕建. 实数齐次核下的Pachpatte型不等式[J]. 华南师范大学学报(自然科学版),2013,45(2):42-46.
HUANG Y J. On Pachpatte-type inequalities with a real number homogeneous kernel[J]. Journal of South China Normal University(Natural Science Edition),2013,45(2):42-46.
[4] 卢钰松,王五生. 一类含有p次幂的Volterra-Fredholm型非线性迭代积分不等式[J]. 西南大学学报(自然科学版),2015,27(8):76-80.
LU Y S,WANG W S. A class of Volterra-Fredholm type nonlinear iterated integral inequality withppower[J]. Journal of Southwest University(Natural Science Edition),2015,27(8):76-80.
[5] ZHENG B. Explicit bounds derived by some new inequalities and applications in fractional integral equations[J]. Journal of Inequalities and Applications,2014(4):1-12.
[7] 马庆华,杨恩浩. 弱奇性Volterra积分不等式解的估计[J]. 应用数学学报,2002,25(3):505-515.
MA Q H,YANG E H. Estimates on solutions of some weakly singular Volterra integral inequalities[J]. Acta Mathemati-cae Applicatae Sinica,2002,25(3):505-515.
[8] 吴宇. 关于一类弱奇性Volterra 积分不等式的注记[J]. 四川师范大学学报(自然科学版),2008,31(5):534-537.
WU Y. A note on a class of weakly singular Volterra integral inequalities[J]. Journal of Sichuan Normal University(Natural Science),2008,31(5):534-537.
[9] 梁英. 一类时滞弱奇异Wendroff型积分不等式[J]. 四川师范大学学报(自然科学版),2014,37(4):493-496.
LIANG Y. A class of weakly singular Wendroff-type integral inequalities with delay[J]. Journal of Sichuan Normal University(Natural Science),2014,37(4):493-496.
[10]YONG Y. On some new weakly singular Volterra integral inequalities with maxima and their applications[J]. Journal of Inequalities and Applications,2015(1):1-16.
[13]ABDELDAIM A,YAKOUT M. On some new integral in-equalities of Gronwall-Bellman-Pachpatte type[J]. Applied Mathematics and Computation,2011,217:7887-7899.
[14]KUCZMA M. An introduction to the theory of functional equations and inequalities:Cauchy’s equation and Jensen’s inequality[M]. Katowice:University of Katowice,1985.
【中文责编:庄晓琼 英文审校:肖菁】
EstimationofUnknownFunctionofWeaklySingularIteratedIntegralInequality
HUANGChunmiao,WANGWusheng*
(SchoolofMathematicsandStatistics,HechiUniversity,Yizhou546300,China)
A class of nonlinear weakly singular iterated integral inequalities is given. There is a nonconstant term outside the integrals in the integral inequality. The upper bound of the embedded unknown function of the inequalities is estimated explicitly by adopting novel analysis techniques, such as: discrete Jensen inequality, Hölder integral inequality, the techniques of change of variable, and the method of amplification. The derived results can be applied in the study of qualitative properties of solutions of fractional integral equations.
weakly singular triple integral inequalitiesy; discrete Jensen inequality; Hölder integral inequality; analysis technique; estimation of explicit bound
2016-01-13 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
国家自然科学基金项目(11561019,11161018); 广西壮族自治区自然科学基金项目(2016GXNSFAA380090); 广西壮族自治区高等学校科研项目(KY2015ZD103,KY2015LX341)
O
A
1000-5463(2017)04-0111-04
*通讯作者:王五生,教授,Email:wang4896@126.com.

