圆域有理q-Bézier曲线

吕雁燕, 刘 植, 刘晓雁

(1.合肥工业大学 数学学院,安徽 合肥 230009; 2.拉文大学 数学系,加利福利亚 拉文 91750)

圆域有理q-Bézier曲线

吕雁燕1, 刘 植1, 刘晓雁2

(1.合肥工业大学 数学学院,安徽 合肥 230009; 2.拉文大学 数学系,加利福利亚 拉文 91750)

文章基于一类广义Bernstein基函数定义了圆域有理q-Bézier曲线,通过改变参数q的取值,可以得到一类有理q-Bézier曲线簇,并研究了该类曲线的基本性质及De Casteljau型算法,用二次有理q-Bézier曲线可精确表示圆锥曲线。该方法比现有方法更加灵活,且表示范围更大。数值实例表明,圆域有理q-Bézier曲线的研究具有一定的理论意义与应用价值。

圆域算术;圆域有理q-Bézier曲线;中心曲线;De Casteljau型算法;圆锥曲线

曲线和曲面的表示是CAD及CAM重要的研究方向之一。经典Bernstein多项式在函数逼近论、计算几何以及概率论等领域均有着重要的应用。近20年来关于Bernstein多项式的推广研究已取得丰富成果[1]。文献[2]首次提出一类基于q-整数的广义Bernstein多项式,它是经典Bernstein多项式的一种推广形式。文献[3]基于该多项式提出了一类新的多项式基函数,称之为q-Bernstein基,进而得到新的参数多项式曲线——q-Bézier曲线。q-Bézier曲线包括了Bézier曲线,且具有与Bézier曲线类似的性质。参数q的引入赋予了q-Bézier曲线更加丰富的形状控制能力。然而和经典Bézier曲线一样,q-Bézier曲线也不能精确表示除抛物线外的圆锥曲线。文献[4]基于De Casteljau算法研究了有理q-Bézier曲线,并在一定范围内给出了圆锥曲线的有理q-Bézier表示，但其结果并不完整,文献[4]中圆锥曲线的构造只对参数q进行讨论,而忽略了权因子ω。

几何造型中大量运算都是基于浮点运算环境[5],因此几何体的表示不够精确,几何计算也是近似的。为了保证数值运算的稳定性以及计算结果的精确性,人们常采用区间方法[6-7]。 用二维区间代替点进行运算,从而能保证理论上的精确结果含于计算结果中,在一定程度上避免重要信息的丢失。然而,文献[8]指出区间算法有2个缺点:① 区间在计算过程中会逐渐扩大;② 矩形区间在二维空间中不具有旋转对称性,导致区间曲线不再具有仿射不变性。为了克服这些缺点,文献[9]用圆盘代替控制顶点引入了圆域Bézier曲线,该曲线可看作由Bézier曲线上的每一点与相应半径构成的动圆扫过的平面区域。圆域Bézier曲线也可看成一种带误差的Bézier曲线,当所有的圆域半径都相同时即为等距曲线。相对于传统的NURBS曲线,上述各种Bézier曲线克服了基本算法中存在的数值不稳定问题。 有理q-Bézier曲线能精确表示圆锥曲线,因此将圆域Bézier曲线向有理圆域q-Bézier曲线的推广是一件有意义的工作。

本文提出圆域有理q-Bézier曲线的概念,并研究了其基本性质,得到q-Bézier曲线的De Casteljau算法。重点讨论了圆锥曲线带的圆域有理二次q-Bézier表示,通过改变q和ω的取值可以得到更加丰富的圆锥曲线带,并给出参数q以及权因子取不同值时的圆域有理q-Bézier曲线表示圆锥曲线的分类图,拓展了现有方法的使用范围。

1 预备知识

1.1 圆域运算

设R为全体实数集,R+为全体非负实数集,N为全体自然数集。平面圆域

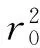
可表示为〈P0〉=〈P0;r0〉。其中,(x0,y0)∈R2，为圆域的中心;r0∈R+，为圆域的半径;P0表示以原点为起点,点(x0,y0)为终点的向量。

对于任意2个圆域〈P1;r1〉、〈P2;r2〉和实数λ∈R,定义圆域运算如下：

λ〈P1;r1〉=〈λP1;|λ|r1〉,

〈P1;r1〉+〈P2;r2〉=〈P1+P2;r1+r2〉。

故n+1个圆域的线性组合可表示为：

(1)

1.2q-Bernstein基

在参数曲线的基表示方法中,基函数具有重要的作用。基于q-Bernstein基的有理q-Bézier曲线是有理Bézier曲线的推广。

对任意n∈N,q∈R+,n次q-Bernstein基函数[3]定义为：

(2)

其中,连乘符号中没有乘积项时视为1;[i]定义为：

q-二项式系数定义为：

特别地,当i=0时,上式为1。

对任意q∈(0,1],q-Bernstein基在区间[0,1]上是一组全正基。四次q-Bernstein基函数曲线(q=0.5)与经典四次Bernstein基函数曲线(q=1)的对比如图1所示。

图1 四次q-Bernstein基与四次Bernstein基

2 圆域有理q-Bézier曲线

2.1 概念

定义1给定n+1个平面圆域〈Pi〉=〈Pi;ri〉和ωi∈R+,i=0,…,n。对t∈[0,1],定义平面n次圆域有理q-Bézier曲线为：

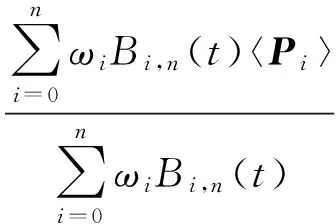
(3)

其中,Bi,n(t)为(2)式定义的n次q-Bernstein基函数;〈Pi〉 (i=0,1,…,n)为控制圆域;ωi(i=0,1,…,n)为权因子。特别地,当ωi为常数时,〈R〉(t)退化为圆域q-Bézier曲线，即

若记

并称之为n次有理q-Bernstein基函数,则由(1)式知,(3)式也可表示为：

〈R〉(t)=〈R(t);r(t)〉,t∈[0,1],

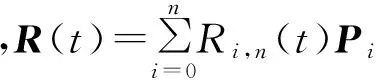
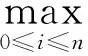
〈Pi〉w={(wix,wiy,wi)∈R3|

在三维空间定义非有理圆域q-Bézier曲线为：

或

其中,t∈[0,1];Bi,n(t)为(2)式定义的n次q-Bernstein基函数。对〈R〉w(t)使用中心投影变换,即得相应的圆域有理q-Bézier曲线。

2.2 性质

圆域有理q-Bézier曲线具有与有理Bézier曲线相似的性质，具体如下:

(1) 端点插值。〈R〉(0)=〈P0〉,〈R〉(1)=〈Pn〉，这是由于

(2) 凸包性。当所有的权因子ωi>0,参数q∈(0,1]时,圆域有理q-Bézier曲线位于控制圆域的凸包内。事实上,

即〈R〉(t)是圆域〈Pi;ri〉(i=0,…,n)的凸组合。

(3) 仿射不变性。圆域有理q-Bézier曲线的中心曲线是一条有理参数q-Bézier曲线,因此它具有仿射不变性。对于圆域半径r(t)，其在平移、旋转、反射条件下依旧成立。

(4) 形状可调性。给定控制圆域和权因子,可以通过改变参数q的取值来调整圆域有理q-Bézier曲线的形状。如给定如下控制圆域：

〈P0;r0〉=〈(9,10);2.3〉,〈P1;r1〉=〈(10,24);3〉,

〈P2;r2〉=〈(18,44);1.5〉,〈P3;r3〉=〈(30,46);2〉,

〈P4;r4〉=〈(35,30);1.5〉;

权因子

ω0=1,ω1=2,ω2=3,ω3=4,ω4=5。

形状参数q=0.1和q=0.9时对应的圆域有理四次q-Bézier曲线如图2所示。

图2 q取不同值时的圆域有理四次q-Bézier曲线

由图2可以看出,参数q的增大使圆域有理q-Bézier曲线更接近控制圆域。

2.3DeCasteljau型算法

(2) 对s=1,2,…,n;i=0,1,…,n-s,计算

类似经典De Casteljau算法,上述算法的中间圆域可表示为:

3 圆锥曲线的精确表示

圆锥曲线是CAD系统中重要的几何造型工具。圆域有理q-Bézier曲线不但可以生成自由形态的曲线曲面,而且能精确表示圆锥曲线。由(3)式可知,二次圆域有理q-Bézier曲线可表示为:

〈R〉(t)=

(4)

其中,B0,2(t)=(1-t)(1-qt)、B1,2(t)=(1+q)×t(1-t)、B2,2(t)=t2为二次q-Bernstein基函数。

为了便于几何描述,本文取

ω0=ω2=1,ω1=ω,

且所有的圆域半径都相等。

首先,当(1-q)+ω(1+q)=0时,(4)式的分母B0,2(t)+ωB1,2(t)+B2,2(t)=(1-t)2+t2恒不为0,二次圆域有理q-Bézier曲线(4)表示椭圆。

其次,当(1-q)+ω(1+q)≠0时,因为

所以可以通过变换控制圆域和权因子,把圆域有理二次q-Bézier曲线表示为圆域有理Bézier曲线的形式。新的控制圆域和权因子分别为:

〈P0′〉=〈P0〉,〈P1′〉=

此时圆锥曲线可以按q和ω的取值分类如下:

(1) 若(ω1′)2<1,即-4<(q+1)(ω-1)<0,则〈R〉(t)表示椭圆。(1-q)+ω(1+q)=0恰好也包含在该结论中。

(2) 若(ω1′)2=1,即(q+1)(ω-1)=-4或者(q+1)(ω-1)=0,则〈R〉(t)表示抛物线。

(3) 若(ω1′)2>1,即(q+1)(ω-1)<-4或者(q+1)(ω-1)>0,则〈R〉(t)表示双曲线。

注意到,当q=-1时,〈P1′〉=〈P0〉,得到一条从〈P0〉到〈P2〉的直线段带。对任意实数ω，ω1′<0,即(1-q)+ω(1+q)<0,得到互补弧线,以相反的顺序遍历。当ω1′<0或q<-1或q>1时,曲线不满足凸包性质。

在几何造型中,上述结果可采用分布图的形式表示,如图3所示。在由q和ω构成的坐标系中,“E” 表示椭圆区域,“H” 表示双曲线区域,位于E和H之间的边界曲线是抛物线区域。 特别地,直线q=1即为经典有理二次Bézier曲线。

图3 圆域有理二次q-Bézier曲线的形状分布图

因此,与有理二次Bézier曲线相比,有理二次q-Bézier曲线表示圆锥曲线的范围更广,除了可以利用ω控制圆锥曲线的形状外,也可以利用q的取值实现。

对于给定的控制圆域〈P0〉=〈(-3,0);0.15〉、 〈P1〉=〈(2,4);0.15〉、〈P2〉=〈(3,0);0.15〉和权因子ω0=ω2=1、ω1=ω,圆域有理二次q-Bézier曲线生成的各种圆锥曲线带如图4所示。图4a为固定q、调整ω得到的圆锥曲线带;图4b为固定ω、调整q得到的圆锥曲线带。

图4 q和ω的取值不同得到各种圆锥曲线带

4 结 论

本文提出圆域有理q-Bézier曲线的概念,改变参数q的取值可以得到一簇圆域有理q-Bézier曲线。给出了圆域有理q-Bézier曲线的基本性质及相应的De Casteljau型算法。与有理Bézier曲线一样,圆域有理q-Bézier曲线也可精确表示各种圆锥曲线。具体给出了圆锥曲线带的圆域有理二次q-Bézier曲线表示方法以及形状分布图,经典有理Bézier方法以及文献[4]的结果均包含在形状分布图中,故本文的方法在几何造型中增加了构造的灵活性,同时拓展了构造的范围。数值实例表明,通过改变参数q和ω的值可以得到更加丰富的圆锥曲线带。

[1] 达买力汗·胡尔曼哈吉,郭清伟.Bézier曲线的扩展及其应用[J].合肥工业大学学报(自然科学版),2014,37(6):764-768.

[2] PHILLIPS G M.Bernstein polynomials based on theq-integers[J].Annals of Numerical Mathematics,1997,4:511-518.

[3] ORUC H,PHILLIPS G M.q-Bernstein polynomials and Bézier curves[J].Journal of Computational and Applied Mathematics,2003,151(1):1-12.

[4] DISIBUYUK C,ORUC H.A generalization of rational Bernstein-Bézier curves[J].BIT Numerical Mathematics,2007,47(2):313-323.

[5] PATRIKALAKIS N M.Robustness issues in geometric and solid modeling[J].Computer-Aided Design,2000,32(11):629.

[6] MUDUR S P,KOPARKAR P A.Interval methods for processing geometric objects[J].IEEE Computer Graphics and Applications,1984,4(2):7-17.

[7] SEDERBERG T W,FAROUKI R T.Approximation by interval Bézier curves[J].IEEE Computer Graphics and Applications,1992,15(2):87-95.

[8] CHEN F L,WU Y.Degree reduction of disk Bézier curves[J].Computer Aided Geometric Design,2004,21(3):263-280.

[9] LIN Q,ROKNE J G.Disk Bézier curves[J].Computer Aided Geometric Design,1998,15(7):712-737.

Diskrationalq-Béziercurves

(1.School of Mathematics, Hefei University of Technology, Hefei 230009, China; 2.Dept. of Mathematics, University of La Verne, La Verne 91750, USA)

Disk rationalq-Bézier curves are presented using a class of generalized Bernstein basis. A family of disk rationalq-Bézier curves can be obtained by changing the value of parameterq. The basic properties of this kind of rational curves are discussed. De Casteljau type algorithm of disk rationalq-Bézier curves is also considered. The quadratic disk rationalq-Bézier curve can be used to represent conic section accurately. The proposed method is more flexible than the existing methods, and it indicates a larger range. Some numerical examples demonstrate that the study of disk rationalq-Bézier curves is of theoretical importance and practical significance.

disk arithmetic; disk rationalq-Bézier curve; center curve; De Casteljau type algorithm; conic section

2016-07-07；

2016-10-25

国家自然科学基金资助项目(11471093);安徽省教育厅自然科学重大研究资助项目(KJ2014ZD30)；中央高校基本科研业务费专项经费资助项目(JZ2015HGXJ0175);安徽省省级质量工程专业综合改革试点资助项目(2012zy007)和名师工作室资助项目(2015msgzs126)

吕雁燕(1993-),女,安徽东至人,合肥工业大学硕士生;

刘 植(1976-),男,安徽金寨人,博士,合肥工业大学副教授,硕士生导师，通讯作者,E-mail:liuzhi314@126.com;

刘晓雁(1962-),女,安徽合肥人,博士,拉文大学教授.

10.3969/j.issn.1003-5060.2017.09.026

TP391.41

A

1003-5060(2017)09-1289-05

(责任编辑 朱晓临)