3自由度单碰振动系统的Lyapunov指数谱和周期泡现象

王 栋，张艳龙，王 丽

（1.兰州交通大学 机电工程学院，兰州 730070； 2.兰州城市学院 数学学院，兰州 730070）

由于系统间隙的存在，动力机械系统中碰撞振动现象时常发生，如高速运行列车的轮轨碰撞、齿轮传动系统的轮齿碰撞、车辆气动控制门关闭时和车辆的碰撞、运行动车上纯净水水桶和固定装置的碰撞等。研究这类系统的动力学行为对系统减振降噪等优化设计具有重要意义。近年来，许多学者研究了碰撞振动系统的非常规分岔和稳定性。

Luo等研究了两自由度含间隙碰撞振动系统的碰撞运动和参数匹配[1]。伍新等研究了3自由度含间隙碰撞振动系统的Neimark-Sacher分岔，并对其进行了反控制[2]。冯进钤等基于图胞映射理论，论述了Duffing碰撞振动系统中擦边诱导激变的全局动力学行为[3]。系统稳定性分析方面，Lyapunov指数谱是判定动力系统运动稳定性和混沌特性的重要工具。目前对光滑动力系统Lyapunov指数谱的研究已经比较成熟。由于非光滑动力系统在非光滑点的Jacobi矩阵不存在，使得光滑动力系统Lyapunov指数谱的计算方法在非光滑动力系统中不再适用。Stefanski等采用同步现象的特性估算了具有不连续性的两个相同离散动力系统的最大Lyapunov指数[4-5]。Souza等通过在碰撞瞬时附加一定的转换条件，将光滑离散动力系统的Lyapunov指数谱计算方法运用到两个特殊碰撞振动系统的稳定性分析中[6]。金俐等利用Poincaré映射分析法得到了一类单自由度碰撞振动系统Lyapunov指数谱的计算方法[7]。Li等利用Poincaré映射分析法得到了一类2自由度双侧约束振动系统Lyapunov指数谱的计算方法[8]。魏艳辉等通过构造的Poincaré映射及其Jacobi矩阵，得到了一类2自由度单碰振动系统的Lyapunov指数谱的计算方法[9]。周期泡现象分析方面，一些学者也开展了部分研究。石建飞等研究了双参数平面下的Duffing系统的Lyapunov指数和分岔特性[10]。Peng研究了迟滞人口模型中的多重分岔和周期泡现象，并分析了系统的稳定性[11]。Yang等分析了需求与供给相互作用的离散经济模型中的周期泡现象和系统稳定性[12]。Gou等研究了双参平面上直齿轮副运动时出现的周期泡现象[13]。对于3自由度碰撞振动系统，由于系统维数的增加，系统的动力学行为更加复杂丰富，Lyapunov指数谱的计算也更加繁琐。现有文献中对3自由度单碰振动系统中周期泡现象的发生以及Lyapunov指数谱的计算鲜有报道。

本文基于车辆气动控制门关闭时和车辆的碰撞、运行动车上纯净水水桶和固定装置的碰撞、运行的机床工作台和行程限位机构的碰撞等工程振动问题抽象简化得到一类3自由度单碰振动系统的力学模型，运用Poincaré映射分析法给出了该系统的Lyapunov指数谱的计算方法，分析了一定参数变化范围下系统的稳定性，并通过数值仿真，结合系统的分岔图和相图，发现了一定参数下系统存在周期泡和混沌泡现象。本文的研究方法在理论上可以推广到更高自由度，但实际计算会很复杂。

1 力学模型

如图1所示。阻尼系数为C1、C2和C3的线性阻尼器和刚度为K1、K2和K3的线性弹簧分别与质量为M1、M2和M3的质块连接，简谐力Pisin(ΩΤ+τ)(i=1,2,3)分别作用于3个质块，质块只作水平方向的运动。当质块M1的位移X1(T)等于间隙B时质块与刚性约束A发生碰撞，碰撞过程由速度恢复系数R确定，并且不计碰撞持续时间。

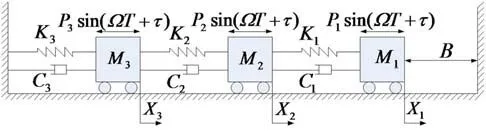
图1 3自由度单碰振动系统动力学模型

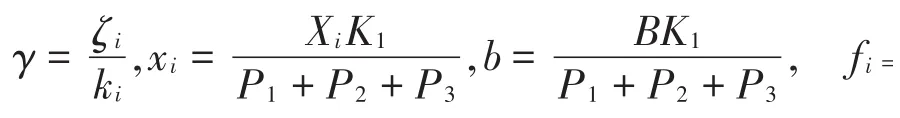
质块M1的冲击方程为

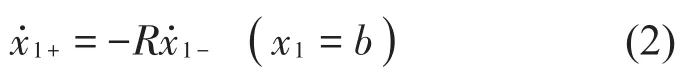
其中：˙1-和˙1+分别为质块M1碰撞前后的瞬时速度。

令Ψ表示方程式(1)的正则模态矩阵，ω1、ω2和ω3分别表示在质块位移(x1＜b)下系统的固有频率。作坐标变换Χ=Ψξ。方程式(1)可解耦为

式中：I是一个3×3阶单位矩阵；C和Λ是3×3阶对角矩阵，且

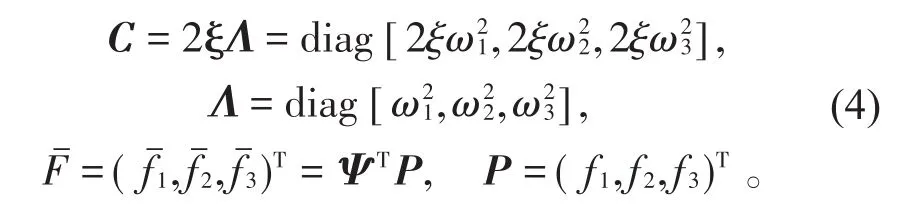
通过模态叠加法可以得到方程式(1)的解为

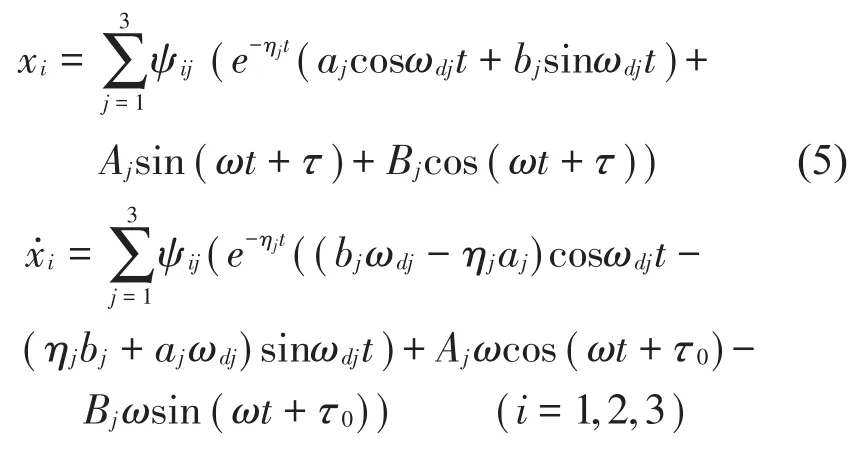
式中：Ψij是正则模态矩阵Ψ的元素；；aj和bj是积分常数，Aj和Bj为振幅常数。令则式(1)可写成如下 1 阶状态方程

2 Jacobi矩阵及Lyapunov指数谱

图2 轨线在相空间穿越Poincaré截面情况

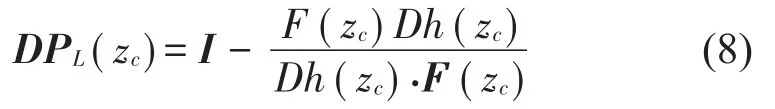
由此可得这几类映射及其Jacobi矩阵：

此映射的切换面为Σ-，方程为h(zc)=x1-b=0，由式(8)可得到局部映射Pa的Jacobi矩阵表达式

(2)映射Pb：Σ-→Σ+

根据质块1的碰撞关系式(2)，可得到局部映射Pb的Jacobi矩阵表达式

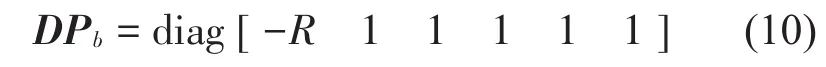
此映射的切换面为定相位面Φφc，切换面方程为φ=φc，由式(8)可得到Pc的Jacobi矩阵表达式

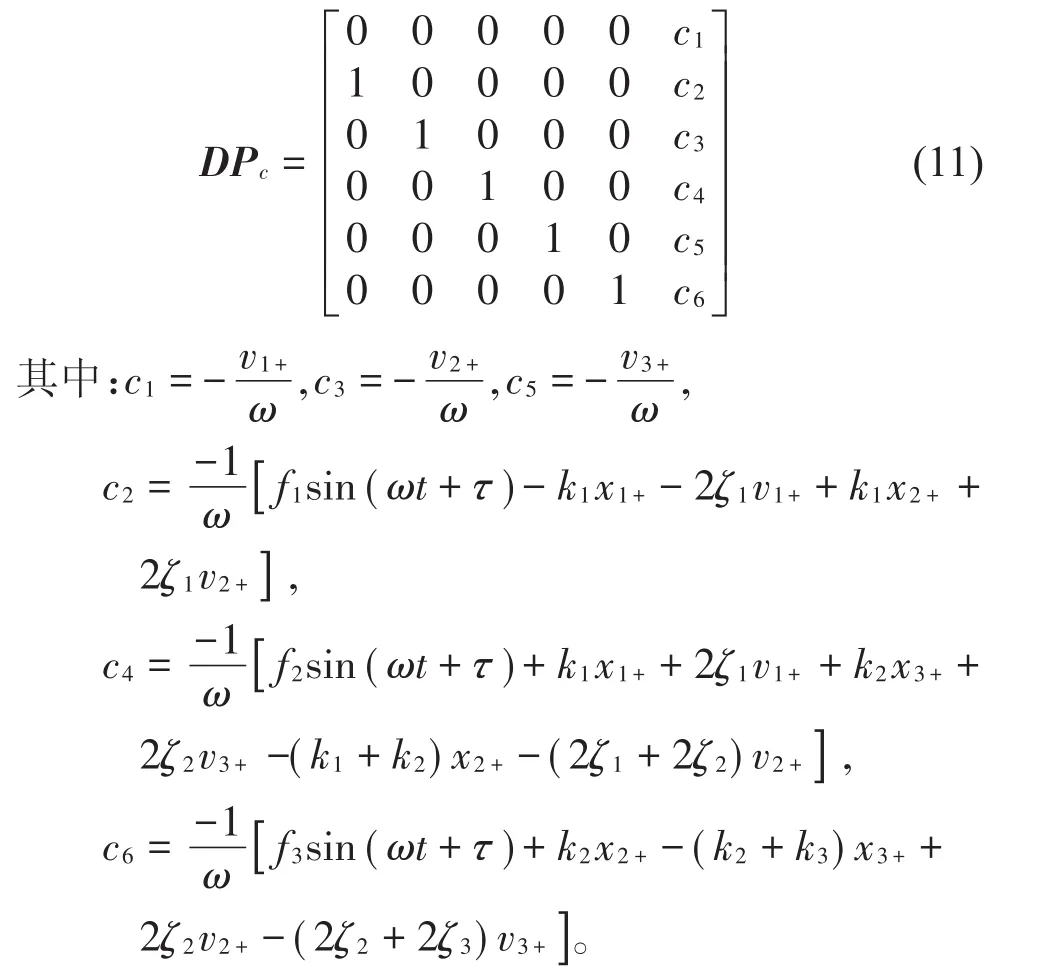
由于该映射所描述的轨线是光滑的，通过数值方法可求得其数值解。其Jacobi矩阵可由多元函数求导法则得到

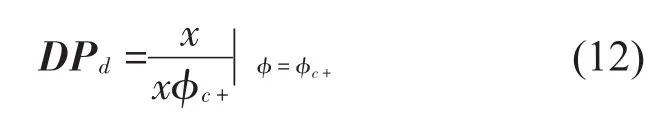
由式(7)定义Poincaré映射P可由以上四种映射复合表示为

根据复合映射求导的链式法则，Poincaré映射P的Jacobi矩阵可写成

3 数值模拟

事先通过选取多组系统参数对系统的动力学行为进行了大量的数值仿真，最终取系统参数m1=1.0，m2=0.4，m3=1.64，k1=1.0，k2=2.0，k3=3.0，γ=0.1，f1=1.0，f2=0，f3=0，R=0.8，b=0.25，在该系统中发现了一种非常规周期结构—周期泡（这种动力学行为在该系统中不常见也不好发现，目前鲜有报道）。为了能够对该系统的周期泡现象作详细分析，用符号q=p/n表示系统对应的周期碰撞运动，其中p表示碰撞次数，n表示周期数。系统随参数ω变化时相位分岔图如图3(a)所示，随ω减小，当ω=2.005 2时，系统由1/2周期运动倍化为2/4周期运动；当ω=1.935 4时，进入混沌运动；当ω=1.806 8时，系统运动变为2/2周期运动；当ω=1.804 4时，倍化为4/4周期运动，系统呈现出周期泡形态，最后由逆倍化分岔序列退化为1/1周期运动。分岔图与最大Lyapunov指数谱的对比图如图3(b)所示（灰色的实线为最大Lyapunov指数谱，虚线为零刻度线），最大Lyapunov指数谱如图3(c)所示，相应的各个Lyapunov指数谱的变化如图3(d)所示（λ5与λ6接近）。综合图3(a)、图3(b)和图3(c)可知，系统处于周期运动时最大Lyapunov指数小于零，处于稳定状态；系统处于混沌运动时，最大Lyapunov指数大于零，处于不稳定状态；当系统周期运动发生分岔时(ω=2.005 2，1.804 4，1.765 2，1.686)，系统的最大Lyapunov指数为零。

图3 系统的分岔图和Lyapunov指数谱

现在来进一歩分析图(3)系统的动力学行为与稳定性。图4(a)为质块1在ω=1.776时对应的4/4周期运动相图，图4(b)为该频率下的Lyapunov指数谱的收敛情况（虚线为零刻度线，λ5与λ6接近），可以得到4/4周期运动对应的最大Lyapunov指数小于零。图4(c)为质块1在ω=1.9对应混沌运动相图。图4(d)为该频率下的Lyapunov指数谱的收敛情况（λ3与λ4接近，λ5与λ6接近），可以得到混沌运动对应的最大Lyapunov指数大于零。

通过数值仿真发现，该系统的周期泡现象对参数m3很敏感，参数m3的微小变动使得系统的周期泡数量变化甚至消失。为了更好的了解参数m3对系统动力学行为的影响，取系统参数m3=1.7，m3=1.68，m3=1.62，m3=1.61，m3=1.607，m3=1.606，m3=1.601 4，其余参数保持不变，系统随参数ω变化时速度分岔图如图5所示。

随着ω的增大，图5(a)所示系统从1/1周期运动倍化为2/2周期运动，随后进入混沌运动；图5(b)所示系统从1/1周期运动倍化为2/2周期运动，再从2/2周期运动倍化为4/4周期运动，随后由4/4周期运动退化为2/2周期运动，最后进入混沌运动，系统呈现出两个周期泡结构；图5(c)所示系统从1/1周期运动倍化为2/2周期运动，再从2/2周期运动倍化为4/4周期运动，然后从4/4周期运动倍化为8/8周期运动，接着经逆倍化分岔序列退化为2/2周期运动，系统呈现出四个周期泡结构；图5(d)所示系统从1/1周期运动经倍周期分岔序列倍化为16/16周期运动，接着从16/16周期运动经逆倍化分岔序列退化为2/2周期运动，系统呈现8个周期泡结构；图5(e)所示系统从1/1周期运动经倍周期分岔序列倍化为32/32周期运动，然后又从32/32周期运动经逆倍化分岔序列退化为2/2周期运动，系统呈现16个周期泡结构；图5(f)所示系统从1/1周期运动经倍周期分岔序列进入混沌运动，随后又从混沌运动经逆倍化分岔序列退化为2/2周期运动，系统呈现16个混沌泡结构；图5(h)为图5(g)的局部放大图，图5(g)所示系统从1/1周期运动经倍周期分岔序列进入混沌运动，随后从混沌运动进入周期运动，接着再次进入混沌运动，然后又从混沌运动进入周期运动，最后进入混沌运动后经逆倍化分岔序列进入2/2周期运动。

图4 质块1在ω=1.776与ω=1.9的相图及Lyapunov指数谱收敛序列

进一歩对图5(d)所示系统出现的周期泡现象作详细分析。图6为图5(d)所示系统中质块1在不同频率下的相图。图6(a)为质块1的1/1周期运动对应的相图；图6(b)为质块1的2/2周期运动对应的相图；图6(c)为质块1的4/4周期运动对应的相图；图6(d)为质块1的8/8周期运动对应的相图；图6(e)为质块1的16/16周期运动对应的相图。

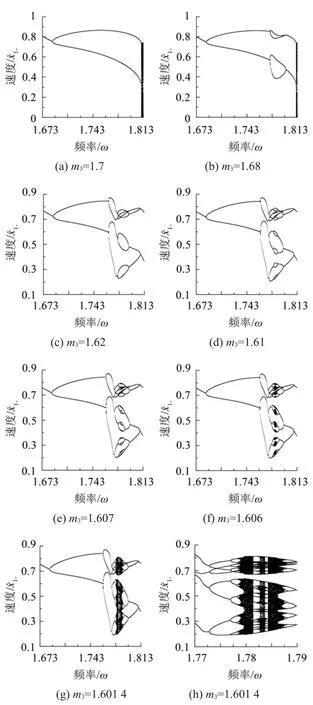
图5 系统随m3变化的速度分岔图及局部放大图

进一歩对图5(f)所示系统的混沌泡现象作具体分析，图5(f)的局部分岔图如图7(a)所示，对应的最大Lyapunov指数谱如图7(b)所示。由图7(b)可知，在系统周期运动发生分岔处（ω=1.761 12，1.773 36，1.778 4，1.780 32，1.785 6，1.788 24，1.794 48）对应的最大Lyapunov指数为零。当系统进入混沌运动，即出现混沌泡现象时，对应的Lyapunov指数大于零，系统失稳。

4 结语

本文引入局部映射，得到Poincaré映射和Jacobi矩阵，通过Gram-Schmidt正交化和范数归一化的方法得到3自由度单碰振动系统Lyapunov指数谱的计算方法。结果表明，利用系统的Lyapunov指数谱，可以有效地对系统的稳定性进行分析。通过数值仿真，结合系统的分岔图和相图，发现在一定参数下系统出现周期泡、混沌泡等丰富的动力学行为。在其他参数保持不变的情况下，随着质量比的减小，系统结构发生改变，系统运动的周期泡结构数量成倍增多，即系统运动的周期数在成倍增加，接着周期泡结构消失出现混沌泡结构，最终混沌泡结构消失系统进入混沌运动。

图6 质块1在不同频率下的相图

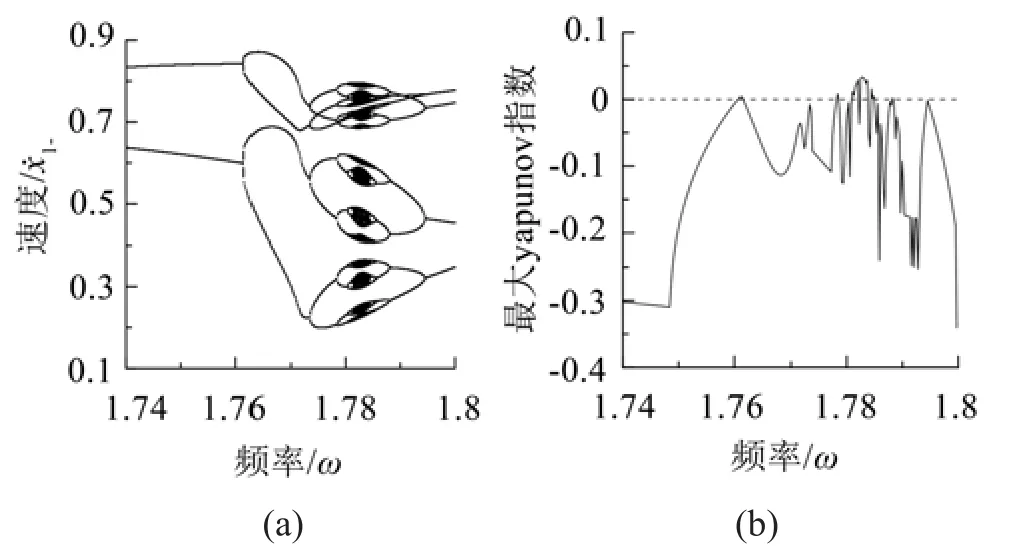
图7 分岔图局部放大图和Lyapunov指数谱