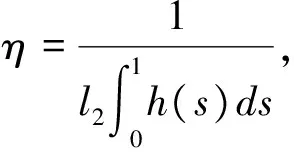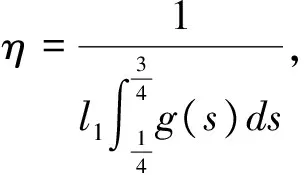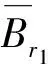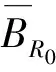一类三阶微分方程多点边值问题两个正解的存在性

高 扬

(大庆师范学院教师教育学院，黑龙江大庆 163712)

1 引言

常微分方程的边值问题在物理学和力学等领域有着重要应用.一直以来，常微分方程边值问题的正解存在性受到了广泛关注，而其中关于三阶m点边值问题的多个正解存在性的研究并不多见[1-3].

本文考虑如下的一类三阶常微分方程多点边值问题:

(1.1)

应用锥拉伸与压缩不动点定理可知，边值问题(1.1)至少存在两个正解.

为了方便起见，先做如下假设：

(H2)h:(0,1)→[0,+)连续，h(t)不恒为0，允许在t=0及1处奇异，且0

(H3)f:[0,+)→[0,+)连续.

2 引理

引理2[3]函数g(t,s)，满足下面不等式

其中，

证明 由引理2及G(t,s),k(t,s)的定义可知，

P={u∈C[0,1]|u(t)≥0,t∈[0,1]}，

则P是C[0,1]上的一个正锥.取

定义算子

引理4[3]若满足假设(H2)～(H3)，则算子A:P1→P1是全连续的.

3 主要结果

定理1 若满足假设(H1)～(H3)且

(3.1)

(3.2)

其中，λ1是前面给出的算子T的第一特征值.

如果存在R0>0，使得

f(u)<ηR0，∀0≤u≤R0，

(3.3)

证明 由(3.1)和(3.2)可知，存在0

f(u)≥λ1u，∀0≤u≤r1，

以及r2>R0，使得

假设A在∂Br1∩P1和∂Br2∩P1上无不动点.否则结论成立.

类似引理5和引理6的证明，可得i(A,Br1∩P1,P1)=0，i(A,Br2∩P1,P1)=0.

∀u∈∂BR0∩P1，由(3.3)及引理3有

故

‖Au‖≤‖u‖，∀u∈∂BR0∩P1.

由引理1知

i(A,BR0∩P1,P1)=1.

因此

定理2 若满足假设(H1)～(H3)，且

(3.4)

(3.5)

其中，λ1是前面给出的算子T的第一特征值.

如果存在R0>0，使得

f(u)>ηR0，∀0≤Ju≤R0.

(3.6)

假设A在∂Br1∩P1和∂Br2∩P1上无不动点.否则结论成立.

类似引理5和引理6的证明，可知

i(A,Br1∩P1,P1)=1，i(A,Br2∩P1,P1)=1.

∀u∈∂BR0∩P1，由(3.6)及引理3有

故

‖Au‖≥‖u‖，∀u∈∂BR0∩P1.

由引理1可知

i(A,BR0∩P1,P1)=0.

因此

[1]周韶林,薛亚娣.一类奇异三阶m点边值问题多个正解的存在性[J].西南大学学报:自然科学版,2010,32(7):22-25.

[2]吴红萍.一类非线性三阶三点边值问题的多个正解[J].贵州大学学报:自然科学版,2014,31(2):4-6.

[3]赵微.一类三阶常微分方程m点边值问题的正解存在性[J].数学的实践与认识,2013,43(20):255-259.

[4]郭大钧.非线性泛函分析[M].济南:山东科技大学出版社,2001.

[5]Zhang G,Sun J.Positive solutions of m-point boundary value problems[J].Math. Anal. Appl.,2004(291):406-418.