立体几何解题策略的再探究
朱小扣 周 园
(1.安徽省无为县牛埠中学 238351;2.安徽省舒城县万佛湖镇中心学校 231360)
立体几何题是高考的重要考点之一,每年高考题中都会出现,约为20分左右.而学生在解答中,容易失误失分,经常会出现“会儿不对,对而不全”的现象,为此笔者现对其答题策略做如下探讨.
一、补形法
补形法虽类似于三视图中的模型法,但用法有区别,补形法更注重局部和整体的联系,特别是在做立体几何的大题时,不补形的话,犹如在“云里雾里”,有时补形后,答案一目了然.

(Ⅰ)试确定点M的位置,使AC∥平面MDF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面MDF将几何体ADE—BCF分成的较小部分与较大部
分的体积比.

图1
解析(Ⅰ)当M是线段AE的中点时,AC∥平面MDF,证明如下:
连结CE交DF于N,连结MN.由于M、N分别是AE、CE的中点,所以MN∥AC.
所以AC∥平面MDF.

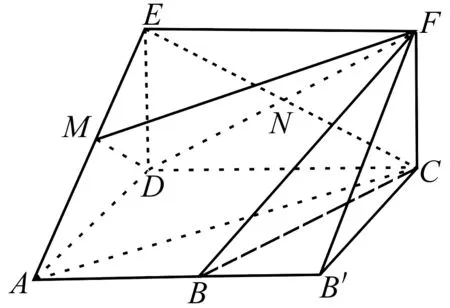
图2
二、颠倒法
在数学解题中经常会要求变换角度,颠倒法就是其中一种,通过颠倒可以将不熟悉的图形转化成熟悉的图形,这是对知识能力的深度考察.虽然颠倒法简单,但绝不应被忽视.
例2 (2016山东理17改编)在如图3所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.

解析可以将图3颠倒成图4.
(1)证明:设FC的中点为I,连接GI,HI,在△CEF中,因为G是CE的中点,所以GI∥EF.又EF∥OB,所以GI∥OB.在△CFB中,因为H是FB的中点,所以HI∥BC.又HI∩GI=I,OB∩BC=B,所以平面GHI∥平面ABC.因为GH⊂平面GHI,所以GH∥平面ABC.

图3 图4



上述两大策略是对文[1]的策略的应用举隅,除此之外,还有如下策略:
三、分割法
分割法是一种求体积的方法,往往是把一个不规则的几何体通过分割,划分成锥体与柱体的组合体.实际上命题者想通过分割,对学生掌握体积公式知识的考查,以及对化归能力的一种提升.

图5
例3 (景德镇市2017届高三上学期期末考试)斧头的形状叫楔形,在《算数书》中又称之为“郓都”或“壍堵”:其上底是一矩形,下底是一线段.有一斧头:上厚为三,下厚为六,高为五及袤为二,问此斧头的体积为几何?意思就是说有一斧头形的几何体,上底为矩形,下底为一线段,上底的长为3,下底线段长为6,上下底间的距离(高)为5,上底矩形的宽为2,则此几何体的体积是( )
A.6 B.10 C.16 D.20
解析如图6所示,过点A作AM⊥EF,垂足为M,连接MD.
过点B作BN⊥EF,垂足为N,连接NC.
则三棱柱ADM-BCN为直三棱柱,三棱锥E-ADM与三棱锥F-BCN全等.
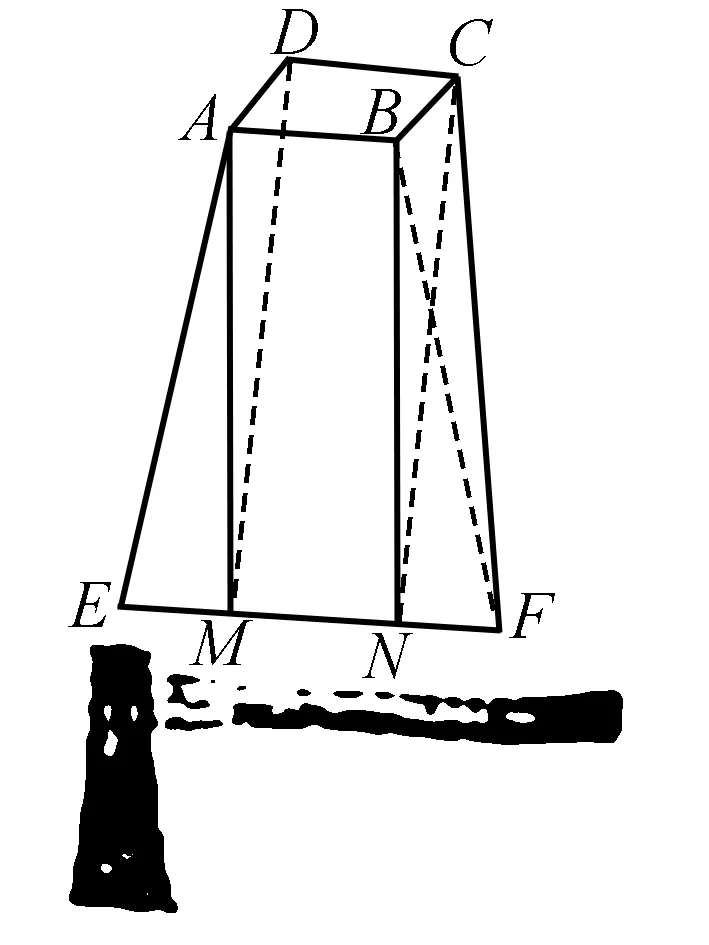
图6
点评像例3中,不仅对中国古代数学文化考察,又考察了分割法,要在短时间内准确地对图形做出分割,实属不易.“分割路不易,且行且谨慎”.
四、模型法
模型法一直是三视图中的一种重要的方法,可以弥补部分同学的空间想象能力的不足,利用模型可以解决线段,角度,体积等问题.



图7

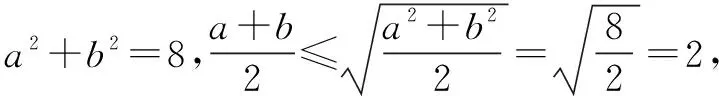
点评像例4,不用长方体模型的话,几乎很难做出来,有人形容三视图问题是“横看成岭侧成峰”,但我们只要站在长方体的“肩膀”上,就会“一览众山小”.
总结遇到立体几何问题时,原则上可以用上面的策略解决.五种策略的运用能很好地锻炼学生的思维.立体几何题目千变万化,但只要掌握其本质,就能一招制敌.同样学生在做题时,必须具有一题多解,多题一解的能力,这样才能在做题时,多角度,多思维的去考虑,才能在做题中达到自身水平的提高.
参考文献:
[1]朱小扣.解决立体几何的三种方法[J].数理化解题研究,2016(28).

