变化中的不变量*
——谈立体几何中的折叠问题

●

(浙江师范大学附属中学，浙江 金华 321004)

在近几年数学高考的立体几何题中经常出现折叠问题，由于其涉及平面图形和空间图形，因此对学生的空间想象、识图及分析能力都提出了较高要求.在考试中此类问题得分率都不高，分析其原因，首先是学生的空间想象力较弱，其次是学生对这类问题没有形成解题的模型和方法.

解决折叠问题的关键在于画好折叠前后的平面图形与立体图形,抓住两个图形的特征关系，并弄清折叠前后哪些量发生了变化、哪些量没有发生变化，以及确定动点在底面上的投影位置，这是分析和解决问题的依据.

教师在数学课堂教学中处理折叠问题的两大策略：1)引导学生用草稿纸演示折叠过程，注意折叠前后的不变量；2)利用数学软件动画演示折叠过程.让学生形象直观地得出折叠问题的3个特征如下：

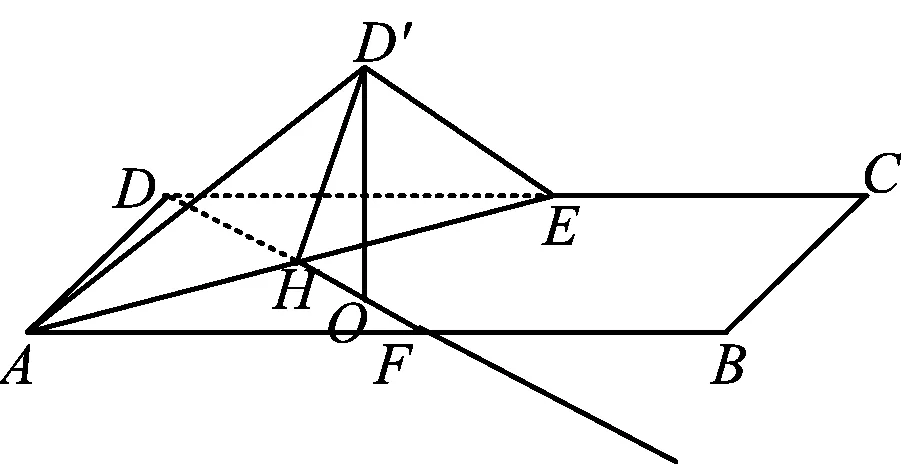
图1

如图1，将△DAE沿AE折成△D′AE，过点D作DF⊥AE交AE于点H,交AB于点F，则

①点D′在底面ABCE上的投影O一定在射线DF上；

②D′H⊥AE,FH⊥AE,∠D′HF是二面角D′-AE-B的平面角；

③折叠后的不变量：在折线同侧的量，折叠前后不变，如D′A=DA,D′E=DE.

笔者通过一些实例，对立体几何中的折叠问题的解题策略作归纳，供大家参考.

1 利用折叠前后的不变量的特征解题

图2

1)求二面角A′-FD-C的余弦值；

2)点M,N分别在线段FD,BC上，若沿直线MN将四边形MNCD向上翻折，使点C与点A′重合，求线段FM的长.

(2010年浙江省数学高考理科试题第19题)

分析1)略.

2)建立如图2所示的直角坐标系，设FM=x，则M(4+x,0,0).翻折后，点C与点A′重合，从而CM=A′M(折叠前后的不变量)，于是

得

即

评注本题是一个两次折叠问题，经历的是一个由动态到静态的过程.要解决此类问题，首先要清楚地知道折叠前后哪些量产生了变化、哪些量没有变化.第2)小题学生的得分率较低，究其原因是学生往往将目光聚焦在第二次翻折后的空间几何图，而忽视了该空间图与原平面图之间联系，即翻折前后CM长度的不变性.求解这类问题要注意对变化前后线线与线面位置关系、所成角及距离等加以区别比较，在“变”与“不变”之间灵活解题.

例2如图3，在矩形ABCD中，已知AB=2，AD=4，点E,F分别在AD,BC上，且AE=1，BF=3，将四边形AEFB沿EF折起，使点B在平面CDEF上的射影H在直线DE上.

1)求证:CD⊥BE;

2)求线段BH的长度；

3)求直线AF与平面EFCD所成角的正弦值.

(2016年浙江省金华十校调研数学试题第17题)

图3

1),3)略.

2)解法1设BH=h,EH=k，过点F作FG⊥ED于点G.因为线段BE，BF在翻折过程中长度不变，根据勾股定理得

即

图4

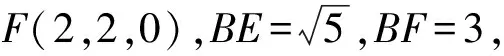
解得

于是B(0,1,2)，故线段BH的长度为2.

评注本题是笔者参与命题的一道高三期末试题.第2)小题学生的得分率很低，究其原因是没有抓住问题的本质——线段BE，BF在翻折过程中长度不变.

2 利用折叠后动点投影的特征解题

例3如图5，在长方形ABCD中，AB=2，BC=1，E为DC的中点，F为线段EC(端点除外)上一动点.现将△AFD沿AF折起，使平面ABD′⊥平面ABC，在平面ABD′内过点D′作D′K⊥AB，K为垂足.设AK=t，则t的取值范围是______.

(2009年浙江省数学高考理科试题第17题)

图5

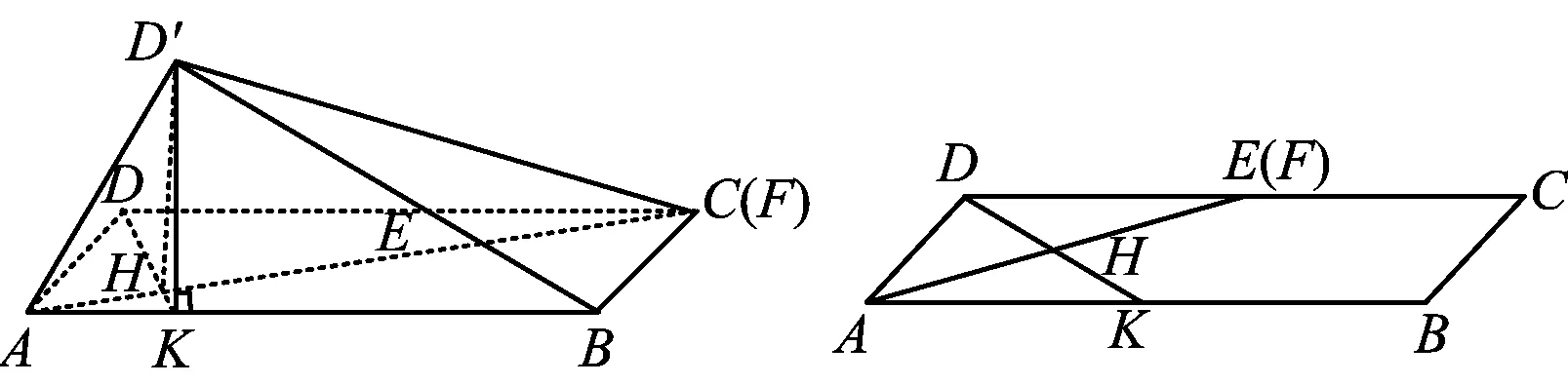
图6 图7

评注本题是2009年浙江省数学高考理科试题填空题的最后一题，学生的得分率很低.若能抓住折叠后动点D′在底面上的投影特征，问题本质就是由折叠引起的二面角D′-AF-B的平面角∠D′HK的变化，再利用两个极端值，得到结果.

( )

A.存在某个位置，使得直线AC与直线BD垂直

B.存在某个位置，使得直线AB与直线CD垂直

C.存在某个位置，使得直线AD与直线BC垂直

D.对任意位置，3对直线“AC与BD”“AB与CD”“AD与BC”均不垂直

(2012年浙江省数学高考理科试题第10题)

当AC=1时，直线AB与直线CD垂直.故选B.

3 利用折叠问题的三大特征解题

例5(原创题)如图8，已知边长为4的正方形ABCD，E是边AB的中点，将△ADE沿DE折起至△A′DE(如图9)，若△A′CD为正三角形，则二面角A′-CD-B的大小是______.

图8 图9

分析如图10，在正方形ABCD中，过点A作AF⊥DE，交DE于点H,交BC于点F.取CD的中点G,联结EG交AF于点O，按题意折叠后的图形如图11所示，可知点A′在底面BCDE上的投影在AF上.又因为△A′CD为正三角形，所以点A′在底面BCDE上的投影也在EG上，从而点A′在底面BCDE上的投影是AF与EG的交点O.联结A′G,因为A′G⊥CD，OG⊥CD,所以∠A′GO就是二面角A′-CD-B的平面角.

故

∠A′GO=30°.

图10 图11

评注本题的关键是要确定点A′在底面BCDE上的投影O的位置.根据折叠问题的3个特征知点O一定在射线OF上，再根据对称性可知点O也在EG上，因此点O是AF与EG的交点.

折叠问题看似变化多端,实则有规律可循.一般情况下，在折线同侧的量，折叠前后不变；“跨过”折线的量，折叠前后可能会发生变化，这是解决这类问题的关键.

本文选取的5个例题都是压轴题，难度较大.在数学教学中，教师若能引导学生对折叠前后图形的元素进行分析，抓住这个动态变化过程中不变的量,如垂直关系、平行关系、长度关系等,充分利用折叠问题的3个特征，抓住折叠问题的解题关键,问题就迎刃而解了.