幻方可以分解为两个正交拉丁方的线性组合

董朦朦，刘兴祥，田雨禾

(延安大学 数学与计算机科学学院， 陕西 延安 716000)

J.Dénes和A.D.kecdWell[1]在1988年的American Mathematical Monthly中发表了题为“A Conjecture Concerning Magic” 的文章,提出了问题： “任何幻方是否都能表示为两个正交方阵之和，其中之一为行拉丁方，另一个为列拉丁方。”历年来,关于矩阵的分解已有很多方法[2-7]，但对幻方的分解还尚未研究。本文应用幻方、行拉丁方、列拉丁方以及正交拉丁方的定义，结合矩阵分解知识对幻方进行分解。

1 预备知识

定义1[8]若矩阵A=(aij)m×m∈Fm×m满足：

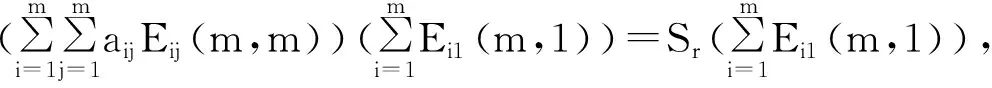
则称矩阵A为数域F上的m阶和幻方,并称S为m阶和幻方A的幻和;Sc为m阶列和幻阵A的列幻和;Sr为m阶行列和幻阵A的行幻和。

定义2[9]设矩阵A=(aij)m×m∈{a+1,a+2,…,a+m2}m×m,a∈Z,若矩阵A满足

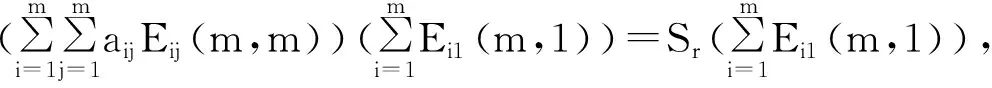
④ aij=akl(i≠k或j≠l, i, j, k, l=1,2,…,m)。

则称矩阵A为数域F上的m阶连元和幻方,并称S为m阶连元和幻方A的幻和。

定义3[9]设矩阵A=(aij)m×m∈{1,2,…,m2}m×m,若矩阵A满足

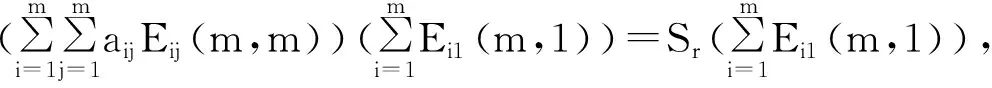
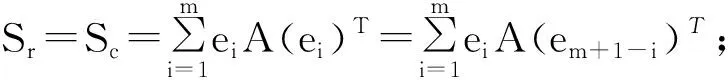
④ aij=akl(i≠k或j≠l, i, j, k, l=1,2,…,m)。

则称矩阵A为数域F上的m阶始元和幻方，并称S为m阶始元和幻方A的幻和。

定义4[10]设矩阵A=(aij)n×n∈Sn×n,n∈N*,其中S={x1,x2,…,xn},对于∀i,j∈{1,2,…,n},i≠j时有xi≠xj,满足以下条件：

① 若∀i,j,k∈{1,2,…,n},且j≠k有aij≠aik恒成立;

② 若∀i,j,k∈{1,2,…,n},且i≠j有aik≠ajk恒成立。

则称矩阵A=(aij)n×n为S上的n阶拉丁方。

定义5[2]设矩阵A=(aij)n×n∈Sn×n,n∈N*,其中S={x1,x2,…,xn},对于∀i,j∈{1,2,…,n},i≠j时，有xi≠xj,且∀i,j,k∈{1,2,…,n},有j≠k时，aij≠aik恒成立,则称矩阵A=(aij)n×n为S上的n阶行拉丁方。

定义6[10]设矩阵A=(aij)n×n∈Sn×n,n∈N*,其中S={x1,x2,…,xn},对于∀i,j∈{1,2,…,n},i≠j时，有xi≠xj,且∀i,j,k∈{1,2,…,n},i≠j时，aik≠ajk恒成立,则称矩阵A=(aij)n×n为S上的n阶列拉丁方。

定义7 设矩阵A=(aij)n×n、B=(bij)n×n∈Sn×n是两个n阶拉丁方,若对于序偶阵C=⎣(aij,bij)」n×n中,对于∀i,j∈{1,2,…,n},当i≠k或j≠l时,(aij,bij)≠(alk,blk)恒成立,则称矩阵A和矩阵B正交,或称矩阵A与B是互相正交的矩阵。

注：下文所用ei均为n维行向量。

2 主要结论

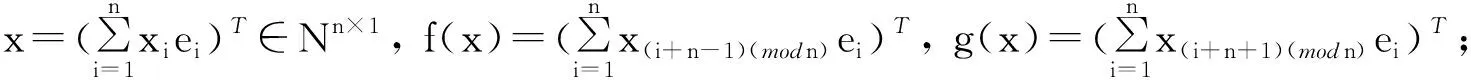
证明先证矩阵A满足幻方的条件。

1) 当n=2k+1时,对由定理1构造出的矩阵

观察知：矩阵B的各行的元素都是1,2，…，2k,2k+1的全排列,故称矩阵B为n阶行拉丁方。

2) 对由定理1构造出的矩阵

观察知：矩阵C的各列的元素都是0,1,2,…,2k-1,2k的全排列,故称矩阵C为n阶列拉丁方。

下面证明矩阵A中的元素是{1,2,…,n2}的全排列。

4) 因为矩阵B中的元素满足1≤bij≤n,矩阵C中的元素满足0≤cij≤n-1,则矩阵nC中的元素满足0≤ncij≤n2-n,所以矩阵A=nC+B中的元素满足1≤aij≤n2且有∀i,j,k,l∈{1,2,…,n2}，aij≠akl,则矩阵A中的元素是{1,2,…,n2}的全排列。综上所述,矩阵A是一个n阶始元幻方。

下面证明行拉丁方B和列拉丁方C是正交的。

5) 构造序偶阵D=⎣(bij,cij)」n×n。假设矩阵B与C不是正交的,则存在数对(bij,cij)=(bkl,ckl),则必有ncij+bij=nckl+bkl,即有n(cij-ckl)=bkl-bij。又因为矩阵B、C中元素满足1≤bij≤n,0≤cij≤n-1,所以有|cij-ckl|≤n-1,|bkl-bij|≤n-1。若ckl-cij≠0,则必有bij-bkl>n,这与|bkl-bij|≤n-1矛盾，故cij=ckl,bij=bkl。此时,若i=k,则有bij=bkl,这与矩阵B是行拉丁方矛盾；若j=l,则有cij=ckl,这与矩阵C是列拉丁方矛盾；若i≠k且j≠l,则有aij=akl,这与矩阵A是幻方矛盾。

故假设不成立,矩阵B与C正交。

证明先证矩阵A满足幻方的条件。

1) 当n=4k时，对由定理2构造出的矩阵

观察知：矩阵B的各行的元素都是1,2，…，4k-1,4k的全排列,故称矩阵B为n阶行拉丁方。

2) 对由定理2构造出的矩阵

观察知：矩阵C的各列的元素都是0，1,2,…,4k-2,4k-1的全排列,故称矩阵C为n阶列拉丁方。

4) 因为矩阵B中的元素满足1≤bij≤n,矩阵C中的元素满足0≤cij≤n-1,则矩阵nC中的元素满足0≤ncij≤n2-n,所以矩阵A=nC+B中的元素满足1≤aij≤n2且 ∀i,j,k,l∈{1,2,…,n2}，aij≠akl,则矩阵A中的元素是{1,2,…,n2}的全排列。综上所述,矩阵A是一个n阶始元幻方。

下面证明行拉丁方B和列拉丁方C是正交的。

5) 构造序偶阵D=⎣(bij,cij)」n×n。假设矩阵B与C不是正交的,则存在数对(bij,cij)=(bkl,ckl),则必有ncij+bij=nckl+bkl,即有n(cij-ckl)=bkl-bij。又因为矩阵B、C中元素满足1≤bij≤n,0≤cij≤n-1,所以有|cij-ckl|≤n-1,|bkl-bij|≤n-1。若ckl-cij≠0,则必有bij-bkl>n,这与|bkl-bij|≤n-1矛盾。故cij=ckl,bij=bkl。

此时,若i=k,则有bij=bkl,这与矩阵B是行拉丁方矛盾；若j=l,则有cij=ckl,这与矩阵C是列拉丁方矛盾；若i≠k且j≠l,则有aij=akl,这与矩阵A是幻方矛盾。

故假设不成立,矩阵B与C正交。

证明先证矩阵A满足幻方的条件。

1) 当n=4k+2时,对由定理3构造出的矩阵

观察知：矩阵B的各行的元素都是1,2，…，4k+1,4k+2的全排列,故称矩阵B为n阶行拉丁方。

2) 对由定理3构造出的矩阵

观察知：矩阵C的各列的元素都是0，1,2,…,4k,4k+1的全排列,故称矩阵C为n阶列拉丁方。

4) 因为矩阵B中的元素满足1≤bij≤n,矩阵C中的元素满足0≤cij≤n-1,则矩阵nC中的元素满足0≤ncij≤n2-n,所以矩阵A=nC+B中的元素满足1≤aij≤n2且有∀i,j,k,l∈{1,2,…,n2}，aij≠akl,则矩阵A中的元素是{1,2,…,n2}的全排列。综上所述，矩阵A是一个n阶始元幻方。

下面证明行拉丁方B和列拉丁方C是正交的。

5) 构造序偶阵D=(bij,cij)」n×n。假设矩阵B与C不是正交的,则存在数对(bij,cij)=(bkl,ckl),则必有ncij+bij=nckl+bkl,即有n(cij-ckl)=bkl-bij。又因为矩阵B、C中元素满足1≤bij≤n,0≤cij≤n-1,所以有|cij-ckl|≤n-1,|bkl-bij|≤n-1。若ckl-cij≠0,则必有bij-bkl>n,这与|bkl-bij|≤n-1矛盾。故cij=ckl,bij=bkl。此时,若i=k,则有bij=bkl,这与矩阵B是行拉丁方矛盾;若j=l,则有cij=ckl,这与矩阵C是列拉丁方矛盾;若i≠k且j≠l,则有aij=akl,这与矩阵A是幻方矛盾。

故假设不成立,矩阵B与C正交。

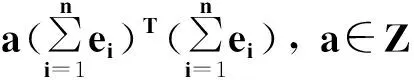
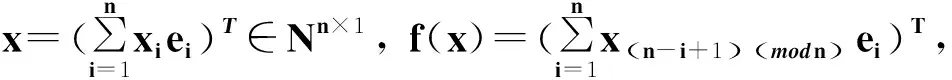
定理4 幻方可以分解为两个正交拉丁方之和，其中之一为行拉丁方，另一个为列拉丁方 (这里行拉丁方指定理中的矩阵B,列拉丁方指矩阵D=nC)。

证明当n=2k+1时,定理1已证；当n=4k+1时,定理2已证；当n=4k+2时,定理3已证。

3 结束语

本文主要研究了始元幻方和连元幻方可以分解为两个正交拉丁方的线性组合，类自然数幻方是否可以作此分解有待进一步研究。