基于向量函数的微分中值不等式
蔡 瑾
(江苏省苏州健雄职业技术学院 215411)
微分形式的不变性以及微分的中值定理作为现代高等数学微分知识中最为基础也是最为关键的一个定理,其微分中值定理以理论基础的方式进行成为了整个微分学的核心理论.因此,此次研究主要从数学分析的角度来了解全微分形式不变性以及微分中值定理,并给出了具体的推广形式.
一、向量函数及微分中值不等式的相关概述
1.向量函数
由于一元函数主要指的是由一个定义域到值域的一个映射,其中的定义域和值域均属于同一维数集,但所要研究的向量值函数却主要指的是分量关于同一自变量的一元函数,也就是n元向量的函数是x到xn上的映射,在此要进行取值的是二维以及三维向量值的函数,也就是当n=2或是n=3时的情况.例如,当平面内进行运动的过程中,其质点在t时刻 的坐标(x,y)可以表述为x=f(t),y=g(t),t∈I,在这种情况下的点(x,y)=(f(t),g(t))所形成的平面曲线C,那么这一点便是质点的运动路径,若是参数方程来进行描述,则是:如果用r(t)表示从以往的质点到该质点的时刻t,位置P(f(t),g(t))的向量,那么r(t)=OP=(f(t),g(t))=f(t)i+g(t)j,其定义式为r(t)=(f(t),g(t),h(t)=f(t)i+g(t)j+h(t)k.
2.微分
微分作为数学中的一个基础定义,延伸出与之相关更多的数学理论知识,微分在数学中的定义主要为:当函数B=f(a)时,得到了A和B的两个数集,在这过程中A中的dx若是逐渐靠近A,那么该函数在dx处的极限为函数在dx处的微分,换句话说,微分的中心思想是无穷分割,作为函数变量中的重要组成部分,微积分的基本概念之一,并主要如图1所示.
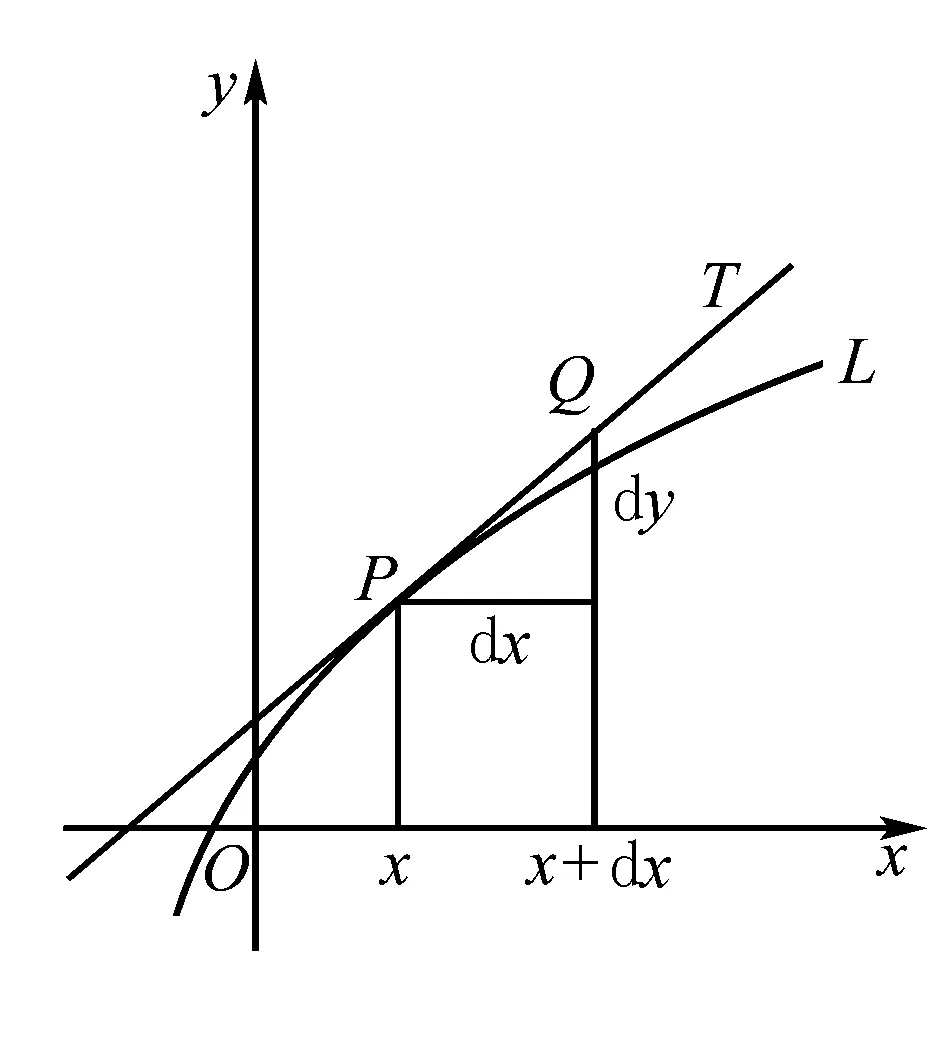
图1
早在希腊时期,人们便已经开始讨论无穷、极限等相关的问题,作为微分的中心思想,这些讨论在目前看来存在一定的漏洞,但却是开启微分理论的第一步,特别希腊时期的阿基米德已经懂得采用无穷分割的方式来正确地计算一些面积,这一做法与现代积分的观念具有一定的相似性,由此可见在历史上的积分的概念要早于微分,其主要定义为每,设函数y=f(x)在x的邻域内存在定义,且x以及Δx+x在此区间内,若是函数增量Δy=f(Δx+x)-f(x)可表示为Δy=AΔx+x.而Δx比x的高阶无穷小,那么函数f(x)在x上是可微的.微分概的存在是为了解决直线与曲线的矛盾中所产生的,并在微小的局部可以采用直线去表示近似代替曲线,这种的直接应用方式为函数的线性化,这说明微分在某种程度上来将是就有双重含义的,微分表示一个微小的量,且这种微小的量可以将线性函数的数值计算结果当做本来函数数值的近似值,作为近似计算的基本思想,微分方法对其完整的呈现出来.
3.微分形式不变性
设函数为y=f(u)时,若是u为自变量,那么函数y=f(u)的微分形式为dy=f′(u)du,若u为中间变量,那么u=g(x),其函数为复合函数,也就是说,自变量为x,即y=f(g(x)),复合函数求导得y′=f′(u),因此,不论u为自变量还是中间变量,均有dy=f′(u)du,这便称之为微分形式的不变性.
二、微分中值定理
微分中值定理作为一系列中值定理的总称,是一种研究函数的重要工具,其主要内容是依据拉格朗日定理为主,更是拉格朗日定理的特殊情况下的推广,微分中值定理在这过程中更好地反映出导数的局部性和函数整体性之间的关系,并得到了较为广泛的应用.设函数y=f(x)在闭区间上连续,并在开区间内可导,则在开区间内至少存在一点ξ,使得f(b)-f(a)=f′(ξ)(b-a),上述公式在向量函数中处于不可导的情况,但却可以证明微分中值不等式在向量函数中的成立,通过相关定理可以得出以下结论:设向量函数r(x)在闭区间上连续,并在开区间内可导,则在开区间内至少存在一点ξ,使得r(b)-r(a)=r(ξ)(b-a).
证明:设a=r(b)-r(a),g(x)=a·r(x),x∈(a,b),由上述公式中可知,实值函数g(x)可以满足上述的条件,且存在ξ∈(a,b),从而得出:g(b)-g(a)=g(ξ)(b-a)=[a·r(ξ)](b-a),又因为g(b)-g(a)=a·r(b)-a·r(a)=a·[r(b)-r(a)]=a2,通过上述两个公式中可以推导,a2=[a·r(b)](b-a)≤a·r(ξ)(b-a),也就说明r(b)-r(a)=r(ξ)(b-a)=a2=[a·r(b)](b-a)≤a·r(ξ)(b-a),证毕.
三、向量函数全微分形式不变性
假设定理A,D∈Rn为凸开集,f为D→Rn,若f可微,则任意两点a,b∈D,所以,存在点ξ=a+θ(b-a),0<θ<1,令‖f(b)-f(a)‖≤‖f(ξ)‖‖b-a‖.本文证明了基于向量函数的微分中值不等式:
定理:假设函数f(z)在凸区域D解析,z1,z2∈D,那么,一定存在ξ=z1+θ(z2-z1),0<θ<1,令‖f(z2)-f(z1)‖≤‖f(ξ)‖‖z2-z1‖.
定理证明:
令f(z)=u(x,y)+iv(x,y),z1=a+ib,z2=a+h+i(b+k),以上数字均为实数,那么,φ(x,y)为实值函数,D内可微,根据函数微分中值定理,令根据Schwarz有
φx(a+θh,b+θk)h+θy(a+θh,b+θk)k≤[φx(a+θh,b+θk)]2+[φy(a+θh,b+θk)]2·h2+k2.
经运算,[φx(a+θh,b+θk)]2+[φy(a+θh,b+θk)]2.
基于Ceuchy-Riemann条件,ξ=aθh+i(b+θk)=z1+θ(z2-z1),
另一方面,φ(a+h,b+k)-φ(a,b)=[u(a+h,b+k)-u(a,b)]2+[v(a+h,b+k)-v(a,b)]2,
于是,|f(z2)-f(z1)|2=|f(z2)-f(z1)|·|f(ξ)|·|h2+k2|,
即:|f(z2)-f(z1)|≤|f(ξ)||z2-z1|.
综上所述,微分形式的不变性以及微分的中值定理作为现代高等数学微分知识中最为基础也是最为关键的一个定理,其微分中值定理以理论基础的方式进行成为了整个微分学的核心理论.与此同时,向量函数及相关的分析性质更是进行几何学习的重要基础和前提,主要是因为向量函数的分析性以及空间几何解析几何之间的重要关系,特别是近年来随着科技的发展和时代的进步,微分几何这种古老但却具有一定先进性和引导性的学科更是逐渐显露出其生命力以及重要的理论研究价值.

