亚纯函数和q-差分多项式分担一个值的唯一性

陆健豪，徐俊峰

（五邑大学 数学与计算科学学院，广东 江门 529020）

1 引言与预备知识

本文使用了Nevanlinna值分布论中的常用记号与基本结论[1]. 本文出现的“亚纯函数”表示在整个复平面上亚纯，(f)表示亚纯函数f的增长级. 若非恒为零的亚纯函数a(z)满足T(r,a)=S(r,f)，此处S(r,f)=o(T(r,f))(r→∞)，除了关于r的一个可能存在有限例外集，我们称a(z)是f(z)的小函数，用S(f)表示全体f(z)的小函数组成的集合.

令f(z),g(z)为两非常数亚纯函数，a(z)为关于f(z),g(z)的小函数，若函数f(z)-a(z)与g(z)-a(z)有相同的零点和相同的重数，称f(z)与g(z)分担a(z)CM，若不考虑重数，则称f(z)与g(z)分担a(z)IM.

为了阐述本文的结论，需要用到以下知识.

定理A亚纯函数f(z)的增长级σ(z)与超级σ1(z)定义为

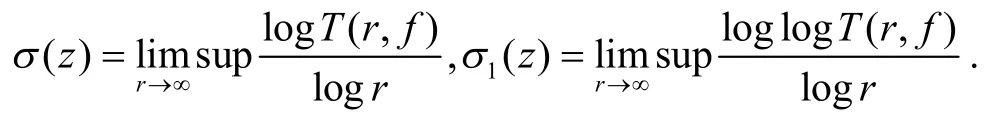
定理B[2]令f为超越整函数，n,k为正整数且n≥k+1，F=fn,Q≡/0为一个多项式，若F-Q与F(k)-Q分担0CM，则F≡F(k)，且f(z)=cewz/n，此处c,w为非零常数，且wk=1.

猜想1令f为超越整函数，n,k为正整数且n≥k+1，Q1,Q2为两不恒为零的多项式，若fn-Q1与(fn)(k)-Q2分担0CM，则进一步，若Q1=Q2，则有f(z)=cewz/n，此处c,w为非零常数，且wk=1.

问题1假如用{f(z+c1)f(z+c2)…f(z+cn)}(k)替换上述猜想中的(fn)(k)又是否成立呢？此处ci(i=1,2,…,n)为常数.

在2016年和2018年，Majumder等人分别在文献[4-5]中证明了猜想1和问题1成立. 得到如下定理.

定理C[4]令f为超越整函数，n,k为正整数且n≥k+1，Q1,Q2为两不恒为零的多项式，若fn-Q1与(fn)(k)-Q2分担0CM，则进一步，若Q1=Q2，则有f(z)=cewz/n，此处c,w为非零常数，且wk=1.

定理D[5]令f为具有有限多个极点的有限级超越亚纯函数，n,k∈ℕ，假如fn(z)-Q1(z)，{f(z+c1)f(z+c2)…f(z+cn)}(k)-Q2(z)分担0IM，且fn(z)与f(z+c1)f(z+c2)…f(z+cn)分担0CM，此处为常数，为不恒为零的多项式，若n≥k+2，则进一步，如果Q1=Q2，则此处λ为非零常数，且

自然地，我们考虑定理D的q-差分形式，得下如下定理：

定理1设f(z)为有限多个极点的零级超越亚纯函数，对任意n,k∈ℕ，若fn(z)-Q1(z)，分担0IM并且分担0CM，此处qi(i=1,2,…,n)为非零复常数，Q1,Q2为两多项式且满足Q1Q2≡/0. 如果n≥k+2，则

定理2设f(z)为有限多个极点的零级超越亚纯函数，对任意n,k∈ℕ，若fn(z)-Q1(z)，[f(qz-c1)f(qz-c2)...f(qz-cn)](k)-Q2(z)分担0IM，此处q,c1,c2,…,cn为非零常数，Q1,Q2为两多项式且满足并且分担0CM，如果n≥k+2，则

2 相关引理

本文定理的证明需要用到下述引理.

引理1[6]令f为非常数亚纯函数，an(z)(≡/0),an-1(z),…,a0(z)为f(z)的小函数，则

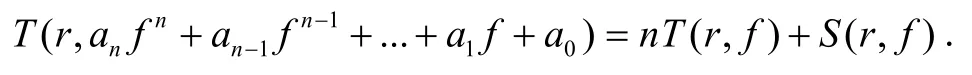
引理2[7]设f(z)为增长级为零的亚纯函数，q为非零复常数，则在一个对数密度为1的集合上成立.

引理3[8]设f(z)为有限级亚纯函数，c为非零复常数，则对于任意ε＞0，有T(r,f(z+c))=T(r,f)+O(rσ-1+ε)+O(logr).

引理4[9]设f(z)为有限级亚纯函数，c为非零复常数，则有

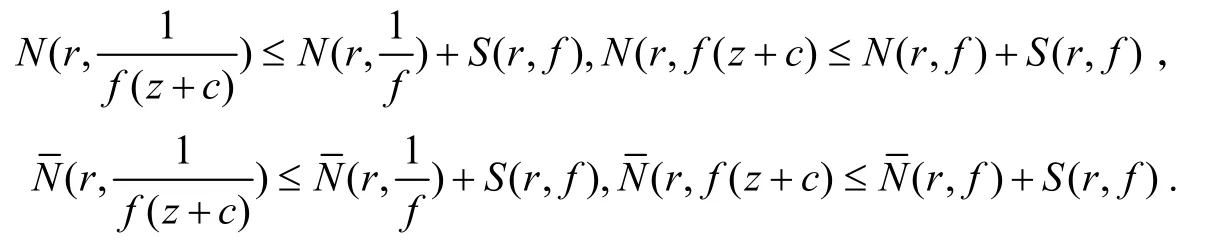
引理5[10]假设F是定义域D上的亚纯函数，令则对n≥1，有此处为一个常系数微分多项式，当n≤3时，此项为零，当n＞3时，此项次数为n-3.

3 定理1的证明

由引理2可得

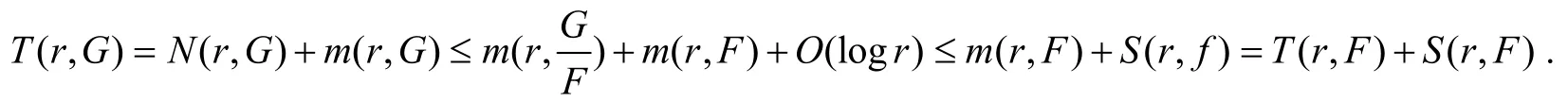
同理也可得到

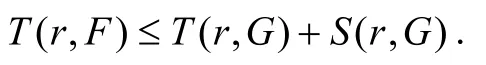
于是S(r,G)=S(r,F)+S(r,f). 因此，由引理2可知

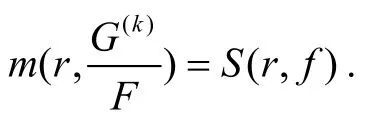
反设F1≡/G1. 于是

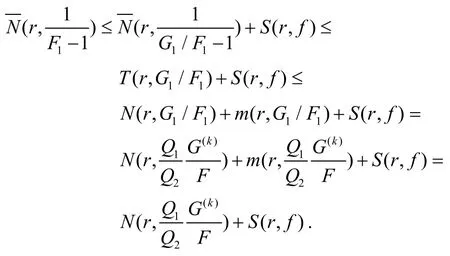
因为F,G分担0CM，且F有有限多个极点，则G(z)=f(q1z)f(q2z)...f(qnz)也有有限多个极点.从而

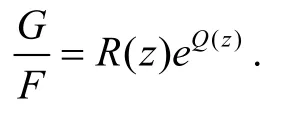
R(z)为有理函数，Q(z)为多项式，从而G=F⋅R(z)⋅eQ(z). 求导可得

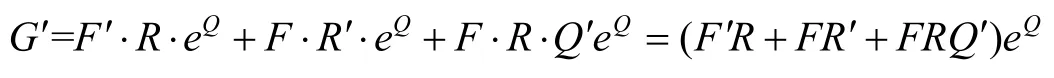
从而

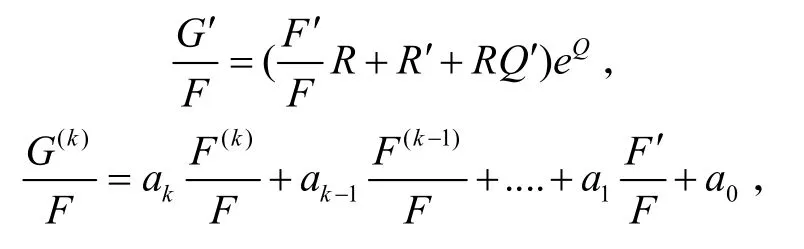
其中ai(i=1,2…,k)是由R,Q,eQ,R(i),Q(i),(eQ)(i)(i=1,2...k)所组成的式子，由此可得，的极点来自及其导数的极点，即

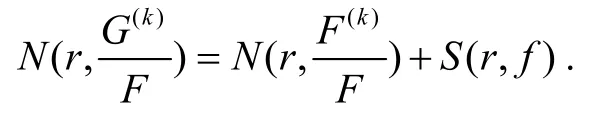
由式（1）、引理1以及第二基本定理可得

由n≥k+2以及式（2）可得矛盾. 从而F1≡G1结论成立.

定理2的证明与定理1类似，不再赘述.