探究圆锥曲线中的最值问题

张妙安

(福建省漳州市第二中学 363000)

圆锥曲线中的最值问题是近年高考中的热点问题，对考生分析、解决问题的能力要求较高，具有一定的难度和区分度.基于此，本文拟通过归类解析的形式，着重帮助同学们理清处理此类问题的常用解题策略，逐步提升解题能力.

一、充分利用圆锥曲线的“定义”

涉及与焦点有关的圆锥曲线中的最值问题，具体求解时往往需要充分利用圆锥曲线的“定义”探求解题思路，有利于将最值问题进行等价转化，以便结合图形或者利用基本不等式顺利分析最值问题.

例1 已知点P是抛物线y2=16x上的一个动点，设点P到定点M(3,4)的距离为d1，点P到抛物线焦点的距离为d2，则当d1+d2取最小值时，点P的坐标为．

解析如图，设点P在抛物线准线上的射影是点N，则由抛物线的定义可知，d1+d2=|PM|+|PN|．

又由图可知当且仅当M,P,N三点共线时，|PM|+|PN|取得最小值．

于是，当d1+d2取最小值时，点P的纵坐标与点M的纵坐标相同，从而可设所求点P的坐标为(m,4)，将之代入抛物线方程y2=16x即得m=1.

故所求点P的坐标为(1,4)．

评注本题求解的关键是，先明确d1+d2取最小值的具体情景是什么，然后再借助图形加以具体分析.

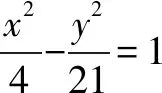
解析由双曲线的定义得|PF1|-|PF2|=4，所以|PF1|=4+|PF2|.

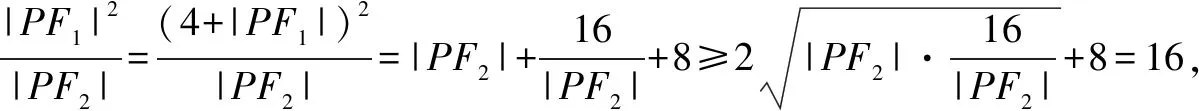
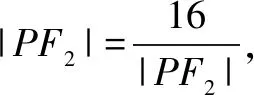
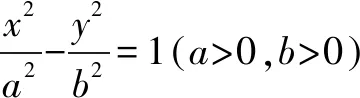
二、紧扣“二次函数”知识加以分析

动点在圆锥曲线上，求解与圆锥曲线的中心、焦点有关的数量积的最值问题时，通过消元，可转化为求解二次函数在某区间上的最值问题；然后再利用“配方法”或“数形结合法”即可顺利获解.

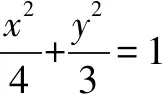
A．2 B．3 C．6 D．8

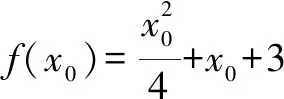
评注本题侧重考查椭圆与向量知识的交汇，解题关键是通过消元，转化为求解二次函在闭区间上的最大值，体现了对所学知识、方法的综合考查.

三、巧妙利用“设而不求”思想

处理圆锥曲线中的有关最值问题时，往往需要设出相关直线的方程以及相关点的坐标，再将直线方程中y=kx+m代入圆锥曲线方程，整理得到关于“x”的一元二次方程，然后利用根与系数的关系、基本不等式或函数观点(构造函数，并利用其单调性)巧求最值.这就是所谓的“设而不求”思想.活用“设而不求”思想，有利于降低运算量，提高解题技能.

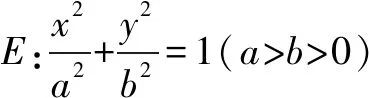
(1)求E的方程；

(2)设过点A的动直线l与E相交于P,Q两点，当△OPQ的面积最大时，求l的方程．

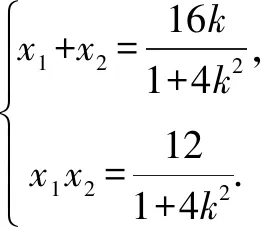
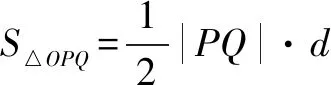
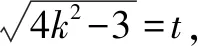
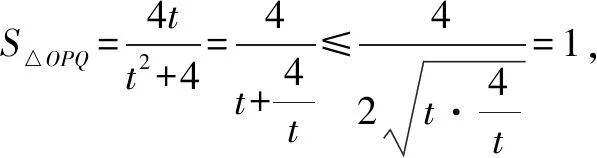
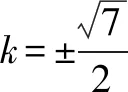
评注本题求解思路是先得到关于“x”的一元二次方程，再考虑最基本的三角形面积公式写出△OPQ的面积的表达式，然后借助换元、基本不等式巧解最大值问题.

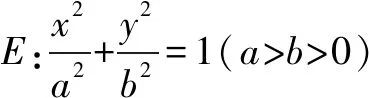
总之，关注处理圆锥曲线中有关最值问题的常用解题策略，有利于积累解题经验，拓宽解题思路，逐步提高求解此类问题的技能技巧.