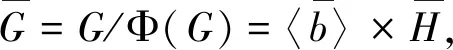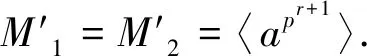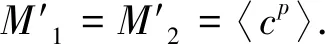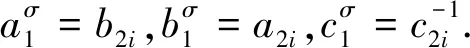极大子群都同构且类二的有限群
豆艾, 李璞金
山西师范大学数学与计算机科学学院, 山西 临汾 041000
0 引言
Berkovich 最早提出研究极大子群都同构的有限群的结构问题[1].极大子群都同构的有限群在历史上被称为 MI 群.由著名的 Sylow 定理可知, MI 群只能是有限p群, 即素数幂阶群.著名群论学家 Hermann、 Mann 等 曾对MI 群做过研究[2~5,8].宋蔷薇等分类了亚循环和超特殊的MI群[6].然而截至目前, 人们只获得了MI 群的某些性质以及某些特定p群类的MI群.而分类 MI 群,仍是一个未解决的难题. 这个问题也被 Berkovich 在其p群专著“Groups of Prime Power Order I”提出, 即下列[7,Problem 77(d)]中的Classify thep-groups all of whose maximal subgroups are isomorphic.
赵立博等研究了pk阶子群都同构且交换的p群(称之为AIk群)并给出了其分类. 显然, 当|G|=pk+1时, AIk群恰是MI 群[8].张勤海研究了pk阶子群都同构且内交换的p群(称之为NSIk群),并给出了其分类. 有趣的是, NSIk群只能是MI 群[9].
我们注意到, 交换群恰是幂零类为1的群.内交换p群是幂零类为 2 的群.反之,幂零类为2 的p群不一定是内交换p群.本文试图研究极大子群都同构且幂零类是 2 的群(称之为C2In-1群),得到了这类群的一些性质. 注意到张勤海分类的是一类特殊的 C2In-1群,本文则完全分类了2元生成的幂零类等于2的C2In-1的有限p群(p>2)[9]. 本文所用符号与文献[10]中符号一致.符号M1 定理1[10,第53页, 定理2.1.4(2)]设G是群,G=〈M〉,则Gn=〈[x1,x2,…,xn],Gn+1|xi∈M〉. 定理2[10,第125页, 定理5.2.2(1)]设G是有限p群. 若c(G) 引理1[11]设G是非交换p群且d(G)=n.不妨设x1,x2,…,xn为G的n个生成元,则G有1+p+p2+…+pn-1个极大子群.它们分别是 其中,ij=0, 1, …,p-1,j=1,2,…,n-1. 有限群G被称为 C2In-1群,如果G的所有极大子群均同构且幂零类为2.显然C2In-1群是MI群,是有限p群.下文定理3给出了一些C2In-1群的性质,定理4给出了2元生成幂零类为2的C2In-1的有限p群(p>2)的分类. 定理3设G是 C2In-1群, exp(G)=pe, 则下列结论成立: (1)c(G)≤3. (2)Z(G)≤Φ(G). (3)G′交换. (4)若Ωe-1(G)≤/Φ(G),则Ωe-1(G)=G. (5)若G正则, 则∀g∈G-Φ(G)都有o(g)=pe. (6)exp(G3)≤p. (7)若exp(G′)=pm, 则G是pm+1交换的. (8)若exp(G′)=pf,e-f>1, 则Ωe-1(G)≤Φ(G). (9)若G是有限2群, 则exp(G′) 证明 (1)∀H (2) 若否, 存在g∈Z(G),M1 (3) 由(1)可知,c(G)≤3.若c(G)=2, 则G′≤Z(G).即得G′交换.若c(G)=3, 则G4=1.任取g1,g2,g3,g4∈G,有[[g1,g2][g3,g4]]∈[G2,G2].由文献[10,定理1.7.14]可知[G2,G2]≤G4=1,即得[[g1,g2],[g3,g4]]=1.于是G′交换. (4) 若否, 则L=Ωe-1(G)Φ(G) (5)设G正则.由文献[10,定理 5.4.11]可知Ωe-1(G)=Ω{e-1}(G). 因此Ωe-1(G) (6)因为G是C2In-1群, 由(1) 可知c(G)≤3.若c(G)=2, 显然成立.若c(G)>2,由文献[12,定理 3.7]即得exp(G3)=p. (7)因为G是C2In-1群,由(1),(6)可知c(G)≤3且exp(G3)≤p.由(3)可知G′交换.于是G亚交换.任取g1,g2∈G, 由文献[10,命题2.1.8] 的计算公式计算可知 即得G是pm+1交换的. (8)由(6)可知,G是pf+1交换的,因而是pe-1交换的.于是Ωe-1(G)=Ω{e-1}(G) (9)因为G是 C2In-1群,由(1),(3) 和 (6) 可知c(G)≤ 3,exp(G3)≤p且G′ 交换.于是存在a,b∈G使得o([a,b])=exp(G′). 若exp(G′)=exp(G)=2e, 由文献[10,命题2.1.8]的计算公式计算可知 这与exp(G)=2e矛盾.故exp(G′) 定理4设G是2元生成且幂零类为2 的有限p群, 其中p>2,则G为 C2In-1群当且仅当G为下列互不同构的群之一 G=〈a,b|apn=bpn=cpr=1,[a,b]=c,[c,a]=1,[c,b]=1〉 其中,n≥r>1. 证明 (⟹)d(G)=2 且c(G)=2的有限p群(p>2)已在文献[14]中分类,见文献[14,定理 3.1]和文献[14,定理3.2].因此只需在上述两个定理的群表中挑出C2In-1群即可. 情形1G为文献[14,定理 3.1]中的群.此种情形下 G=〈a,b|apr+s+u=1,bpr+s+t=apr+s,[a,b]=apr〉 其中,r,s,t,u是非负整数,r≥1,s+u≤r. 情形2G为文献[14,定理3.2] 中的群. 此种情形下,G是下列4类群之一: (1)〈a,b,c|apm=1,bpn=1,[a,b]=c,cpr=1,[c,a]=[c,b]=1〉, 其中,m≥n≥r; (2)〈a,b,c|apm=1,bpn=1,[a,b]=c,cpr=bpt,[c,a]=[c,b]=1〉, 其中 ,m≥n>r,n>t≥(n+r)/2; (3)〈a,b,c|apm=1,bpn=1,[a,b]=c,cpr=aps,[c,a]=[c,b]=1〉, 其中,m>n>r,m>s≥(m+r)/2,n≥m+r-s; (4)〈a,b,c|apm=1,bpn=1,[a,b]=c,cpr=apsbpt,[c,a]=[c,b]=1〉, 其中,m>n>r,m>s>t>r,s+n 参数m,n,r,s,t是正整数,不同参数的群互不同构. 若G为(1)中的群且r=1, 则令M1=〈a,bp,c〉,则M1是交换极大子群.因此G不是C2In-1群,由定理3(5)可知o(a)=o(b)=pn.此时得到本定理中的群. 若G为(3),(4)中的群, 此时o(a)≠o(b). 由定理3(5)可知,G不是C2In-1群.1 预备知识
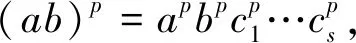
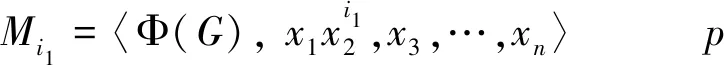
2 2元生成类2的C2In-1群的分类