Hilbert空间中K-Riesz框架的和
黄新丽,朱玉灿
(1.福州理工学院文理学院,福建福州 350506;2.福州大学数学与计算机科学学院,福建福州 350108)
0 引言
Hilbert空间中的框架是文献[1]于1952年在研究非调和级数时引入的概念,是标准正交基的推广,能够将空间中的元素用多种重构表示式线性表出,这种冗余性使其有较高的实际应用价值.目前,框架理论已经在无线电通讯[2]、信号处理[3]等领域有重要的应用.
随着对Hilbert空间中框架理论及其应用研究的不断深入,出现了框架的不同形式的推广.1996年,文献[4]在框架和Riesz基的基础上提出了Riesz框架的概念,并指出利用Riesz框架重构框架系数,可避免无限维空间中框架系数计算复杂的问题.2011年,文献[5]在研究原子分解系统时引入了一种推广框架——K-框架的概念,框架通常在整个Hilbert空间上研究,而K-框架是限制在R(K)上研究,故K-框架比框架更具灵活性且具有实际研究价值.2017年文献[6]进一步提出了Riesz框架的推广——K-Riesz框架的概念,并指出了K-Riesz框架与Riesz框架的不同之处,即Riesz框架一定包含一个Riesz基,但KRiesz框架却不一定包含K-Riesz基.本研究主要讨论K-Riesz框架的和,首先举例说明满足文献[7]中定理3.10的条件时Riesz框架与一个序列的和并不一定为Riesz框架.然后,讨论了由K-Riesz框架与Bessel序列的和构成K-Riesz框架的条件.与文献[8]中定理4.1相比,新增了条件且给出了由两个K-Riesz框架的和构成K-Riesz框架的不同形式的充分条件.最后,文章给出一个K-Riesz框架与一个任意序列的和构成K-Riesz框架的条件.当K=I时,这些结论即为一个Riesz框架与一个序列的和仍为Riesz框架的条件,更正了文献[7]中定理3.10.
1 预备知识
在本研究中,H是一个可分的复Hilbert空间,其内积为〈·,·〉,范数为是H中的恒等算子,N为正整数集,A,B,C,D为正的常数,B(H)是H到H所有有界线性算子的集合.令K∈B(H),且K≠0,用R(K)和NK分别表示算子K的值域和核.l2表示满足的复数列全体所组成的线性空间,特别地对有限子集JN,序列的其他无穷多个元素看作0,则
定义1[5]一个序列称为H的K-框架,如果正数A和B满足
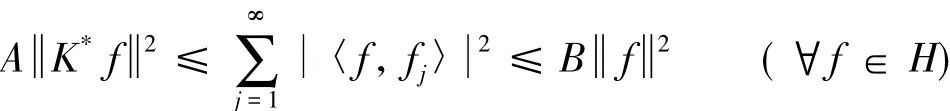
常数A和B分别称为K-框架的下界和上界.特别地,当K=I时,K-框架就是通常的框架.
定义2[6]一个序列称为H的K-Riesz框架,如果存在常数A>0,使得对任意的子集是的K-框架且具有公共的框架下界A.
特别地,当K=I时,K-Riesz框架就是通常的Riesz框架.
定义3[6]设是H的闭子空间,JN,若在W中是完备的且对任意的在 W 中为不完备的,则称在 W 中是极小完备的.

定义有界线性算子如下:

称T,TJ分别为序列的合成算子,且有 R(TJ)=WJ.T,TJ的共轭算子 T*,T*J为
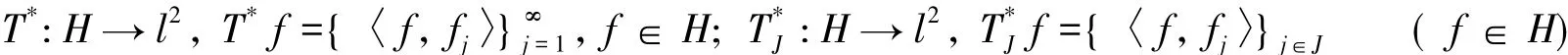
称T*为序列的分析算子.当f∈WJ时,为序列{fj}j∈J的分析算子.
记PR(TJ)为H→R(TJ)的正交投影的正交投影,的正交投影,的正交投影.
为了证明主要结论,需要下面的引理.
引理1[9]设H1和H2是两个复Hilbert空间,T:H1→H2是有界线性算子,T*为T的共轭算子,则
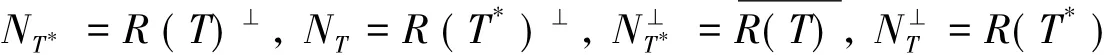
引理2[6]设序列是H的K-框架,则下列陈述等价.
2)存在A>0,使得对任意的有限非空子集JN,若{fj}j∈J在WJ中为极小完备的,则
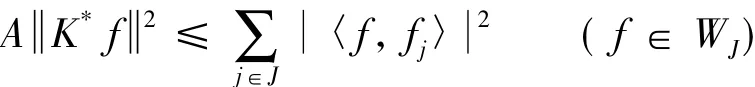
引理3[8]设序列是H的K-框架,T1,T2为相应的合成算子,如果和为正算子,那么为H的K-框架.
引理4[10]假设是的-框架,框架界为,序列H.如果存在常数满足对任意f∈H满足
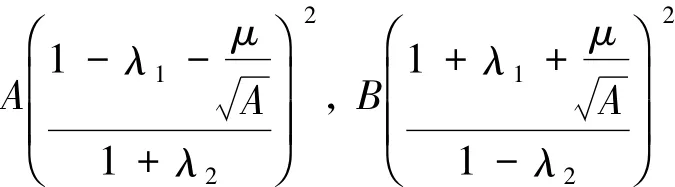
2 K-Riesz框架的和
文献[7]中定理3.10讨论了一个Riesz框架与一个Bessel序列之和仍为Riesz框架的条件,其证明过程中从序列{fj+λgj}j∈J线性无关推出序列{fj}j∈J线性无关.下面举例说明这一推导不正确,进而结论也不成立.
例1设为Hilbert空间H的标准正交基,令序列
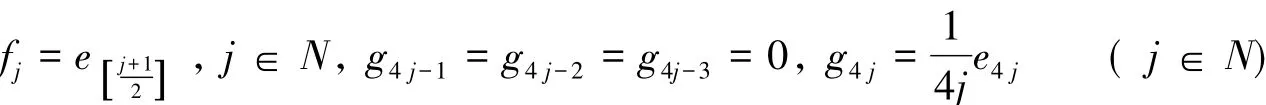
定理1设序列为H的K-Riesz框架,框架界为为H的Bessel序列,界为D,J为N的任意有限非空子集.若为正算子,且,则序列为H的K-Riesz框架.
证明 首先,由已知条件知算子T,U,T*,U*为有界线性算子,且为正算子,取J={1,2,…,n},则对任意的f∈H有:
即TU*+UT*+UU*为正算子.
对任意的 f∈ HJ,令则
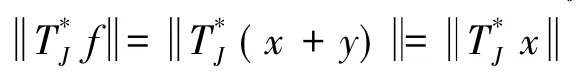
下证{fj+gj}j∈J为HJ的K-框架.由K-Riesz框架的定义得,对任意的f∈WJ有
注1定理1比引理3中新增条件下面举例说明这一条件必须满足,否则定理1的结论不一定成立.例如在例1中,取K=I,λ=1,
定理2设序列为H的K-Riesz框架,框架界分别为A,B,C,D.J为N的任意有限非空子集.若为正算子,且成立,或成立,或NK*和成立,则序列为H的K-Riesz框架.
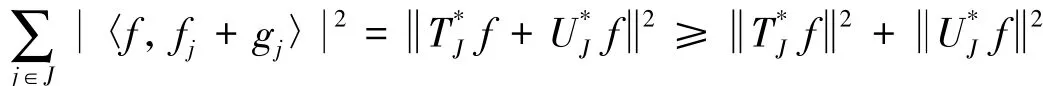
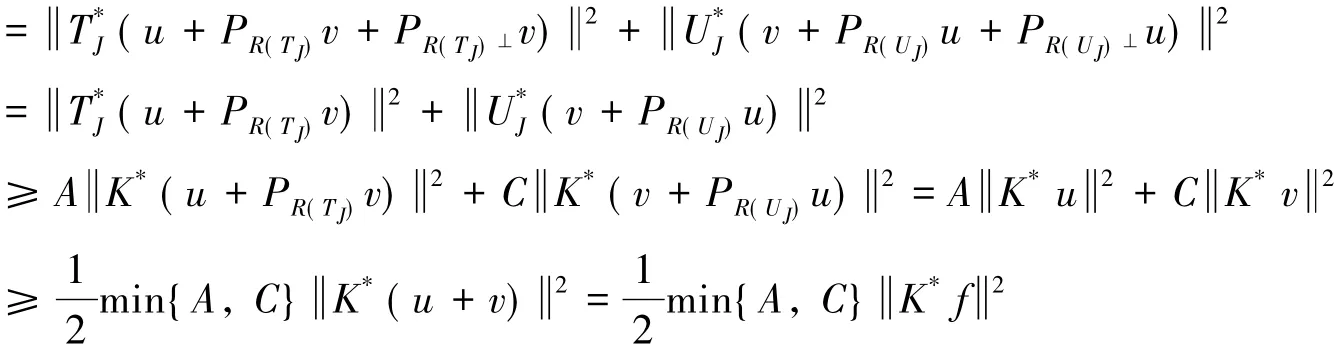
定理3设为H的K-Riesz框架,框架界为是H的一个序列,如果存在常数λ1,λ2∈(-1,1),使得对任意f∈H和任意有限子集JN满足:则序列为H的K-Riesz框架.
证明 在引理4中取μ=0得序列{gj}∞j=1为H的K-框架,框架界分别为下面进一步证明序列为H的K-Riesz框架.
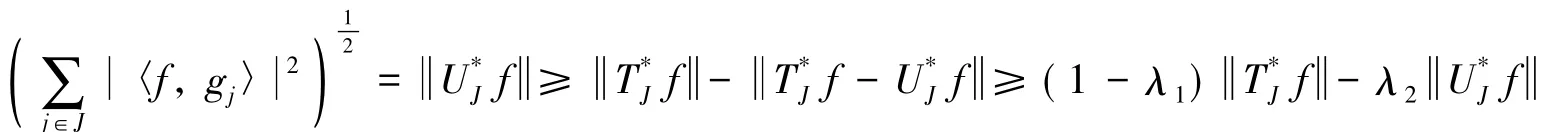
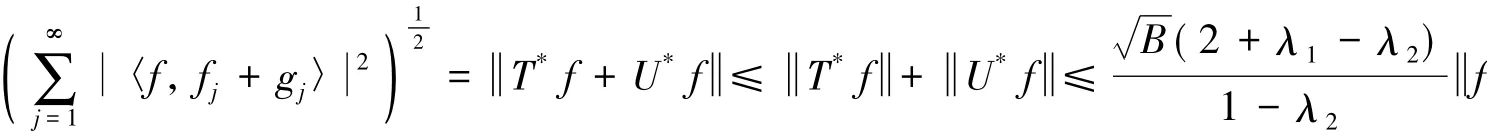
注2当K=I时,上述定理即更正了文献[7]中Riesz框架的相关结论.

