有界变化时滞和联合连通拓扑条件下的分布式无人机编队飞行控制策略

李小民， 毛琼， 甘勤涛， 杜占龙

(1.石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043；2.陆军工程大学石家庄校区 无人机工程系，河北 石家庄 050003；3.63850部队总体研究所，吉林 白城 137001)

0 引言

近年来，无人机编队协同控制在执行战场目标侦查、多目标攻击、跟踪监视、实施电磁干扰和低空突防等方面以其执行效率高、效果好以及灵活性和鲁棒性强等特点，逐渐成为当前无人机领域的研究热点之一。相应的研究方法有领航跟随法、虚拟结构法以及基于行为的方法，这些方法各有优势，但分别存在误差积累、结构不灵活、鲁棒性差以及难以用数学方法分析群体行为等问题[1-2]。近几年发展起来的一致性方法是一种灵活性好、鲁棒性强的分布式编队控制方法，它强调智能体通过获取邻居智能体的状态信息来控制自身的状态，从而实现对整体行为的控制，使编队趋于期望状态。众多学者对一致性理论展开了研究，研究对象的系统模型从1阶和2阶积分系统[3-5]到高阶系统[6-7]、从线性[8-9]到非线性[10-11]、从连续系统到离散系统[12-13]等。由于通信网络的拓扑变化和时滞现象对编队控制有着重要影响，很多文献对此进行了研究，但大多数文献均假设通信拓扑固定[14-17]。文献[18-20]虽然同时考虑了时滞和网络拓扑的动态变化，但是分别针对慢变时滞、线性时滞和定常时滞，对时滞的考虑比较理想。由于受网络带宽、传输速率的限制以及传输可靠性的影响，网络通信中时滞的非线性、快变以及跳变现象时常发生，成为制约多无人机协同控制效果的重要因素；且随着多无人机的运动，其位置的变化会引起编队通信拓扑的动态改变，因此研究通信拓扑切换和复杂时滞变化情况下的编队控制问题更具有较强的现实意义。

虽然由多无人机组成的网络通信时滞变化复杂，但它们一般在有界区间内变化。因此，本文针对多无人机在网络时滞有界和通信拓扑联合连通情况下的编队控制问题展开研究，通过设计基于一致性理论的编队控制策略，采用Lyapunov稳定理论将该策略下的编队飞行控制问题转化为系统稳定性问题加以分析，从而得到实现编队飞行的充分条件，即当系统满足某些线性矩阵不等式条件时，该控制策略能指导无人机编队以期望的目标队形和速度稳定飞行。

1 无人机编队系统动力学建模

考虑由N架无人机组成的编队在三维空间的协同编队飞行控制问题。对编队中第i架无人机进行动力学建模得到：

(1)

(2)

ui(t)与vdi、φdi、χdi之间的关系为

(3)

无人机的性能约束为对状态量Xi以及vdi、φdi、χdi的限定，具体可参考文献[21]中的方法进行处理。

2 图论基础知识

1)Z<0；

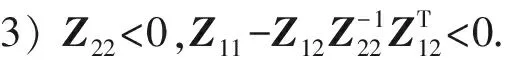
引理2[23]对于任意矩阵W∈Rn×n，0≤τm≤τ1(t)≤τ2(t)≤τM以及向量值函数ω(s)，以下积分不等式成立：

3 控制策略设计与稳定性证明

3.1 基于一致性理论的控制策略设计

对于由N个成员构成的无人机编队，其每个成员在任意时刻需要根据邻居无人机的状态信息来控制和更新自己的当前运动状态。若用无向图描述编队内部各架无人机之间的通信拓扑关系，则由于系统内部的无人机成员在与邻近无人机进行无线通信交换彼此的状态信息(位置、速度)时，受通信带宽、传播速率、通信距离的限制以及外界干扰和环境的影响，其时滞会发生复杂变化，通信拓扑会随着无人机的运动不断切换，在此引进一个分段连续的常值切换函数l(t):[0,∞)|→p={1,2,…,Λ}，简记为l，其中Λ为所有可能的无向通信拓扑总数。

由(2)式可得第i架无人机的动态方程为

(4)

式中：ζi(t)∈R3表示第i架无人机的速度；控制输入量ui(t)设计为

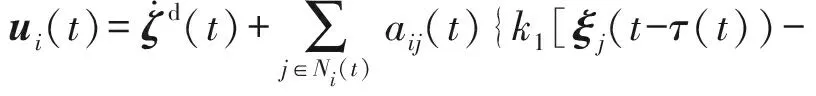
(5)

式中：ζd(t)∈R3表示编队的期望运动速度(根据vdi、φdi和χdi进行解算)；k1、k2、k3为各个分量的控制权重，且k1>0、k2>0、k3>0;τ(t)>0代表t时刻第j架无人机向第i架无人机传递信息时的网络时滞，意味着第i架无人机在t时刻接收到的第j架无人机的状态信息为ξj(t-τ(t))和ζj(t-τ(t))。

多架无人机要形成一定的队形，需要个体在运动时相互之间形成并保持某种相对几何位置关系。为方便描述，设定目标队形中心为编队中心，如图1所示。

图1 无人机编队平面图Fig.1 Plane graph of UAV formation

在图1中，目标编队队形为楔形，Or为其编队中心，O代表笛卡尔坐标系的原点，第i架无人机、第j架无人机和编队中心Or在笛卡尔坐标系中的位置分别为ξi(t)、ξj(t)和ξr(t)，第i架无人机、第j架无人机与Or的距离分别为ri和rj，二者之间的期望位置差值矢量rji=rj-ri，因此rij=-rji.

若第i架无人机在控制量ui(t)作用下其状态[ξi(t)-ξj(t)]→rij且ζi(t)→ζj(t)→ζd(t)，则意味着无人机编队形成期望的目标队形，并以期望的运动速度保持飞行。

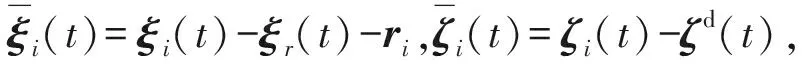
(6)

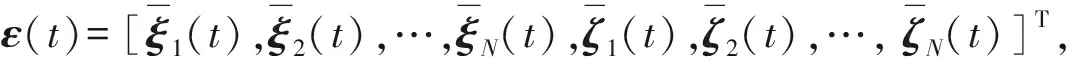
(7)

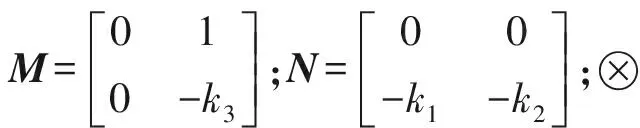
3.2 系统稳定性分析

(8)

(9)

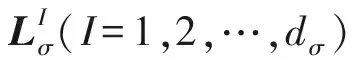
(10)

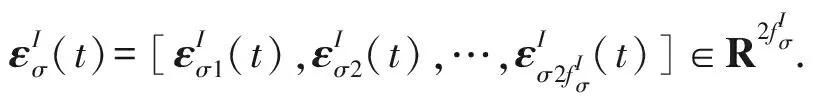
在定理1中，ΞI为对称矩阵，

(11)

式中：*表示ΞI矩阵的对称部分。

令δ=(τh-τl)/2，τa=(τh+τl)/2，则ΞI的其他项表达式如下：

(12)

对(12)式求导，得

(13)

由牛顿- 莱布尼兹公式，

(14)

可将(10)式转化为

(15)

利用引理2，得

(16)

又由于

(17)

式中：-1≤(τa-τ(t))/δ≤1，则

(18)

(16)式和(18)式代入(13)式，得

(19)

再将(15)式代入(19)式并化简为

(20)

下面讨论对于编队内部的所有个体，该恒定值是否为rij. 先假设一个简单情况，编队内部有N-1个个体之间达成了期望的几何位置关系，仅有个体g偏离了期望位置，由于严格受目标编队队形几何关系的约束，导致个体g与其他N-1个个体之间的距离恒定值不等于rgk(k∈(1,2,…,N-1))。根据前面的推导过程可知，个体g在每个重复切换通信拓扑的时间序列内未与其他N-1个个体中的任何一个构成连通关系，这与定理1中的通信拓扑集合联合连通的假设条件是矛盾的，因此该恒定值只能为rgk. 同理，假设个体i与j之间的位置差矢量最终收敛至r且r≠rij，意味着个体i在每个重复切换通信拓扑的时间序列[tk,tk+1)内，未与个体j以及和个体j有连通关系的所有其他个体中的任何一个体构成连通关系；进一步，与个体i有连通关系的任何一个体也未与个体j以及和个体j有连通关系的所有其他个体中的任何一个构成连通关系，即与个体i有连通关系的个体部分和与个体j有连通关系的个体部分不连通，这与定理1中的通信拓扑集合联合连通的假设条件是矛盾的。充分性证明完毕。

4 仿真分析

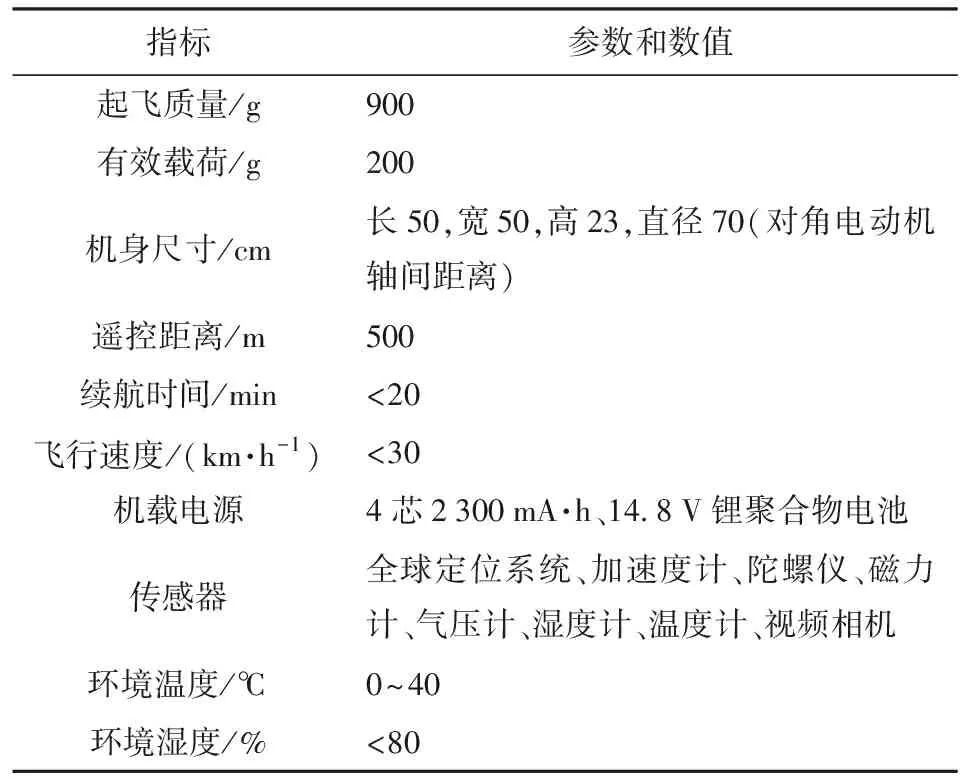
表1 无人机平台的主要性能参数

表2 无人机编队成员的初始状态

4.1 快变时滞条件下的编队控制实现

图2 无人机编队的通信拓扑图Fig.2 Communication topology of UAV formation

图2为5架无人机之间的通信拓扑图，图2(a)和图2(b)均不连通，但其联合图连通。5架无人机的通信拓扑在各个时间子区间按着(G1，G2)的顺序重复切换，每个拓扑图的驻留时间为2 s，每条边权重为1.

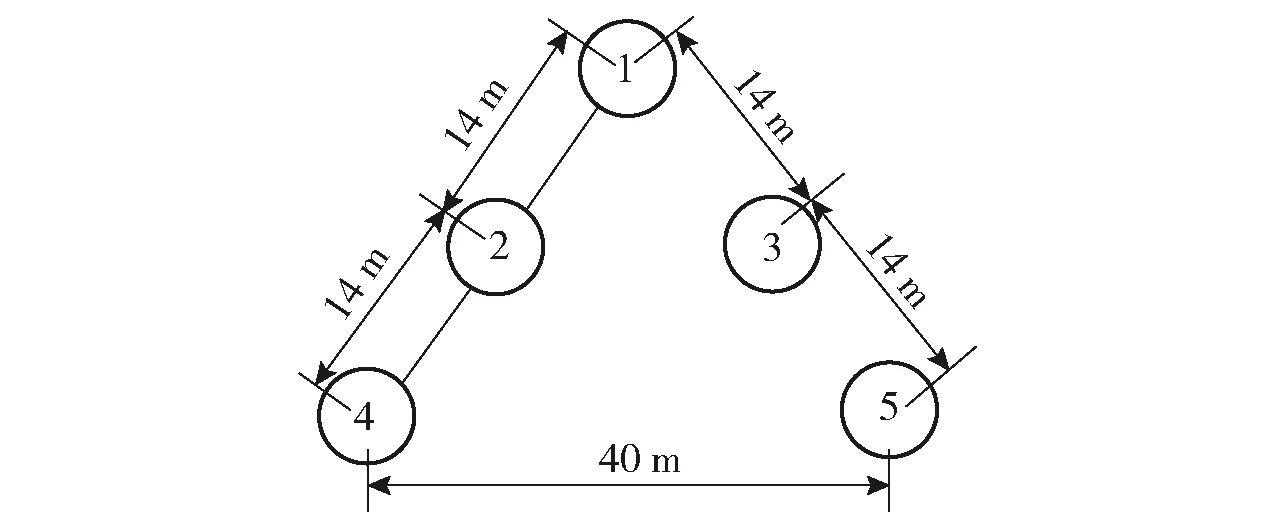
图3 目标编队队形Fig.3 UAV formation

图4 随时间变化的时滞曲线Fig.4 Time delay curve over time

无人机编队成员在三维空间的飞行轨迹、各机的速度、航迹方位角和航迹倾角、各机之间的距离以及控制量随时间变化情况分别如图5～图10所示。

图5 无人机编队在三维空间的轨迹Fig.5 Flight paths of UAV formation in three-dimensional space

图6 编队成员的速度随时间变化曲线Fig.6 Speed-time curves of formation members

图7 航迹方位角随时间变化曲线Fig.7 Flight-path azimuth angle versus time

从图5可知，虽然各架无人机的初始状态不相同，但在控制策略(5)式作用下逐渐靠拢和形成目标楔队形。本文中航迹方位角的定义为飞行速度矢量在地面上的投影与地面坐标轴ogxg轴之间的夹角，以速度向地面的投影在ogxg轴之右时为正；航迹倾角定义为飞行速度矢量与地平面之间的夹角。各机速度(见图6)、航迹方向角(见图7)和航迹倾角(见图8)在图10所示的控制量作用下随着时间的推移逐渐与期望值达成一致，且各机控制量随着目标的达成逐渐趋于0，系统进入稳定状态，即以目标楔队形保持编队飞行。图9进一步表明：各机之间的距离逐渐趋于恒定值，且该恒定值与图3所示目标队形中各成员之间的距离值一致。该实验由于引入了速度、加速度约束，控制量需要在有界区间内作用更持久才能使各机状态与期望值达成一致，它们与时滞一样，不仅延缓了一致性的形成速度，而且使状态量出现了小范围波动；此外，拓扑的切换会诱发控制量的振荡行为，且切换越频繁，带来的高频振荡分量越多。

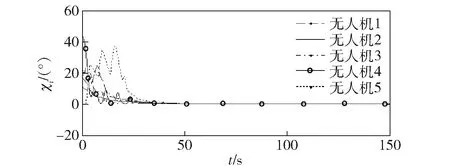
图8 航迹倾角随时间变化曲线Fig.8 Flight-path slant angle versus time

图9 无人机之间的距离随时间变化曲线Fig.9 Distance among UAVs versus time

图10 编队成员的控制量随时间变化曲线Fig.10 Control curves of formation members

4.2 跳变时滞条件下的编队控制实现

5架飞行器的通信拓扑如图11所示，它们各自均不连通，但其联合图连通。各个通信拓扑图的驻留时间为1.5 s，且在各个时间子区间按着(G1、G2、G3、G4)的顺序重复切换，每条边权重为1.

目标队形为图12所示的梯形。5架无人机性能参数和初始状态见表1和表2. 编队成员的期望速度、期望航迹方位角和期望航迹倾角与4.1节相同。

时滞函数τ(t)(随机矩形脉冲)随时间变化的规律见图13. 由于它在有界区间(0≤τ(t)≤2.5)内变化，满足定理1的使用条件，得到一组可行的控制参数k1=0.2，k2=0.6和k3=0.1，使多无人机在控制策略(5)式作用下实现了期望的编队飞行。

无人机编队成员在三维空间的飞行轨迹、各机的速度、航迹方位角和航迹倾角，各机之间的距离以及他们的控制量随时间变化情况如图14～图19所示。

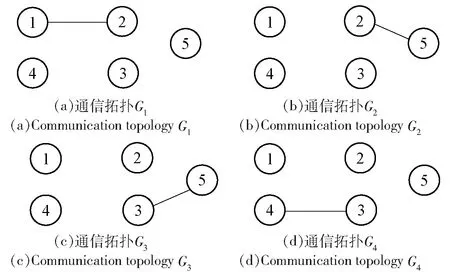
图11 无人机编队的通信拓扑Fig.11 Communication topology of UAV formation

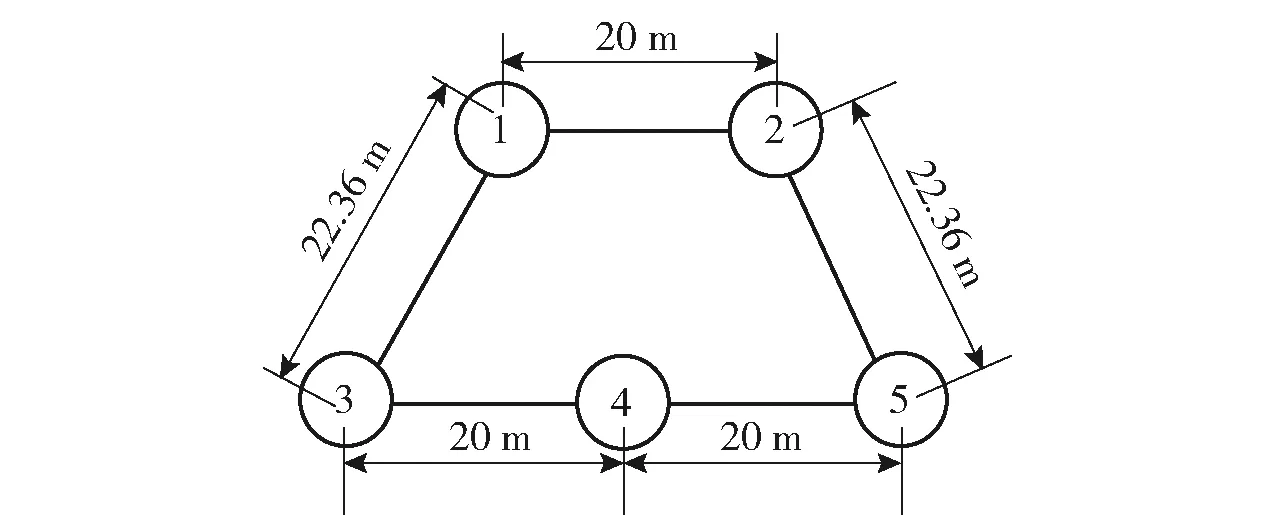
图12 目标编队梯形Fig.12 Trapezoidal formation

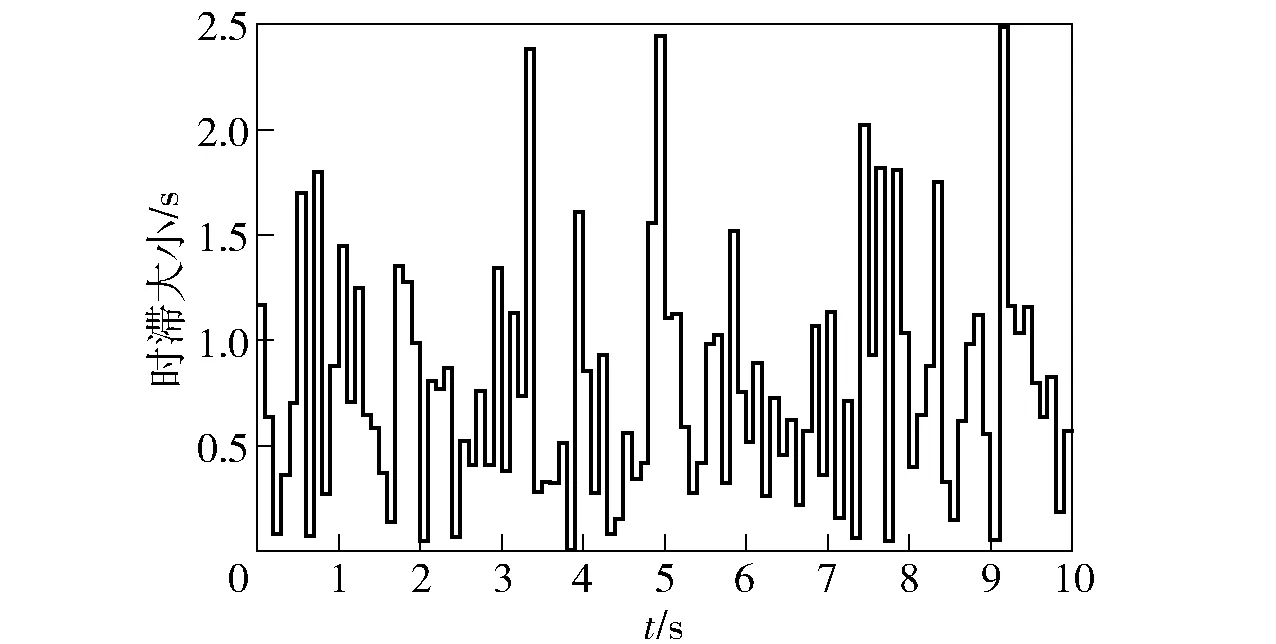
图13 时滞随时间变化曲线Fig.13 Time delay versus time

图14 无人机编队在三维空间的轨迹Fig.14 Flight path of UAV formation in three-dimensional space

图15 编队成员的速度随时间变化曲线Fig.15 Formation members’ speed versus time

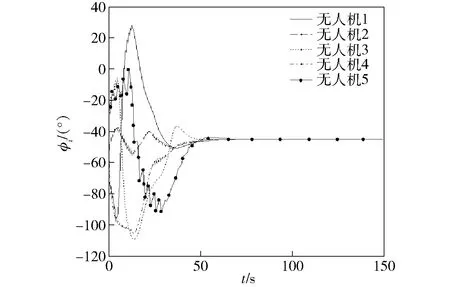
图16 航迹方位角随时间变化曲线Fig.16 Flight-path azimuth angle versus time

图17 航迹倾角随时间变化曲线Fig.17 Flight-path slant angle versus time

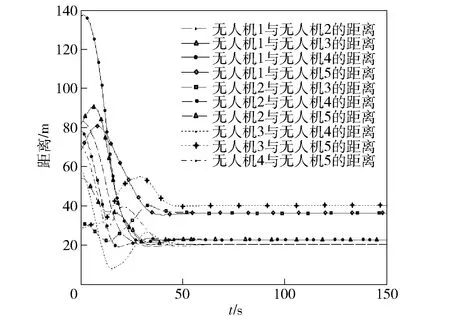
图18 无人机之间的距离随时间变化曲线Fig.18 Distance among UAVs versus time

图19 无人机编队成员的控制量随时间变化曲线Fig.19 Control curves of formation members

由图14～图19可知，虽然网络时滞处于随机跳变状态，但由于其变化有界，编队内部各个成员仍可采用定理1中的方法设计控制策略，并在图19所示的控制量作用下逐渐从初始位置收敛至期望的梯形队形，目标编队形成，并以期望的状态保持飞行，其他结论与4.1节相同。

5 结论

本文针对网络时滞在有界区间变化和通信拓扑动态切换环境下的无人机编队控制问题，在已有控制策略基础上研究了其在复杂环境中控制有效的充分条件。该条件仅需利用时滞变化的上界与下界，就可通过矩阵不等式求解相关控制参数，使得复杂条件下的编队控制成为可行，且具有较大的适用性。该条件仅需对时间子区间内固定通信拓扑图中的连通部分进行计算，相当于把高维数矩阵的求解问题转化为若干个低维数矩阵的求解问题，大幅度减小了计算量，提高了实时性。在将某些物理量的约束(如飞行速度、加速度有界等)引入后，该策略仍然有效，并且可实现任意形状(对称或非对称)的编队构型。