时滞不确定线性系统最优滤波

郭小春

时滞不确定线性系统最优滤波

郭小春

泰山学院信息科学技术学院, 山东 泰安 271021

针对线性时滞不确定系统,应用重组观测分析和完全平方方法,提出了一种简单有效的最优滤波算法。首先将时滞滤波问题转化为非时滞问题,然后通过求解Lyapunov方程以及与原系统维数相同的+1个Riccati矩阵方程,给出滤波器的设计,最后通过一个仿真实例说明该算法的正确性和有效性。

时滞系统; 线性; 滤波

线性最优滤波理论是现代控制理论中的一个基本问题，对于无时滞系统，著名的Kalman滤波理论已经提出了圆满的解决方法，其结果是基于微分或差分Riccati方程设计滤波器[1]。然而对时滞系统的估计问题，经典的Kalman滤波方法已经不再适用。因此，几十年来，线性时滞系统滤波的研究已经引起了专家学者关注，并且已提出许多方法[2-5]，例如线性矩阵不等式方法、状态扩维方法和无限维理论等方法。

不确定性广泛存在于通信系统、网络拥塞控制等许多工程领域，众多学者已对不确定线性系统最优滤波问题提出了不同算法[6-8]。针对观测方程中有相互独立的随机不确定线性系统，Nahi设计出了递推的线性最小方差滤波器[6]。后来Hadidi等人扩展了Nahi的工作，研究了观测中的不相互独立的随机不确定线性系统的滤波问题，同时给出了滤波器的设计算法[7]。Hermoso Carazo等人针对状态噪声和观测噪声都是有色噪声的情况研究了不确定系统的滤波问题，设计出了理想的滤波器[8]。考虑带有随机参数不确定的线性时变系统，应用线性矩阵不等式方法，通过计算一个凸优化问题，Wang和Balakrishnan提出了鲁棒Kalman滤波算法，保证了每一步估计误差的方差最小，同时进一步论证了当状态矩阵是时不变且均方稳定的情况下，该算法是收敛的[9]。应用类似方法，Wang和Balakrishnan又进一步研究了随机不确定系统的鲁棒稳态Kalman滤波问题[10]。不一而足[11-13]。以上所考虑的系统都是非时滞系统。对观测中含有定常时滞的线性系统，应用新息分析理论，有效地解决了最优滤波问题[14-16]。然而，观测中含有定常时滞的线性不确定系统的滤波问题仍需进一步研究。

针对观测中带有多个定常时滞的线性不确定系统，本文将研究最优滤波问题。应用完全平方和观测重组方法，通过计算+1个Riccati方程和一个Lyapunov方程，设计最优滤波器。

为了描述方便，在本文中，给出了如下的符号记号：

（1）表示矩阵转置

（2）R表示实维欧氏空间

（4）[·]表示数学期望

（5）符号⊕表示块对角矩阵

（6）{·}为列向量

1 问题阐述

设带有l个时滞观测的离散时不变系统

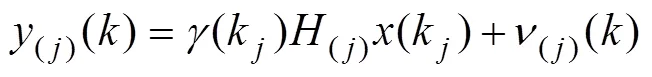
k=-d，=0,1,…,

并满足如下三个假设：

假设1：Prob{(k)=1}=且Prob{(k)=0}=1-.其中为已知常数。

假设2：噪声()，(j)()和初始状态(0)为互不相关的零均值白噪声，且方差分别为

假设3：时滞d，=0,1,…,满足0=0<1<…d.

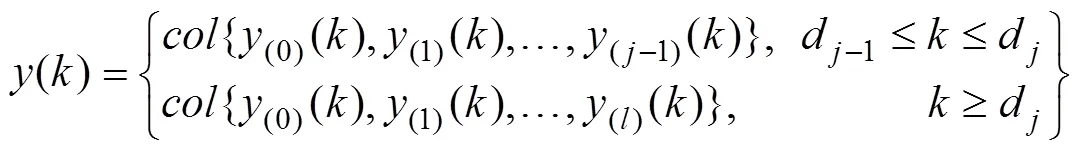
本文问题如下：

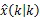
注1：本文所研究的问题广泛存在于信号检测、通讯、网络控制等各种工程领域[7,12]。

注2：对1，原始系统(1)-(2)为非时滞不确定系统,滤波器的设计问题已存在完善的结果[4,5]。因此，本论文主要讨论k≥d时的滤波器的设计问题。

2 滤波器设计

2.1 重组观测

为了设计时滞系统的滤波器，首先重组观测序列，目的是将时滞观测转化成非时滞观测。注意到y(),=1,…,是状态(k)在时刻量测，包含有时滞d，为了使时滞观测转化成非时滞观测，导出重组观测方程

y()=H()()+v()，=+1,…,1 (3)

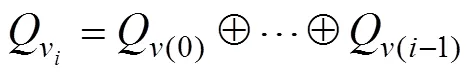
下面引理阐述了原始观测序列与重组观测序列的联系。

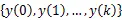
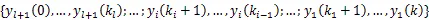
2.2 主要结果

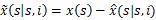
让

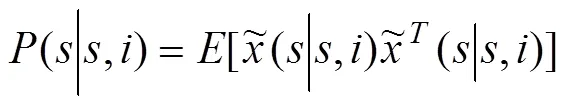
为状态估计误差的协方差矩阵。

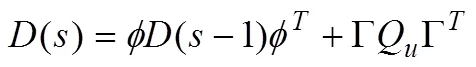
根据上面讨论，给出如下结果。

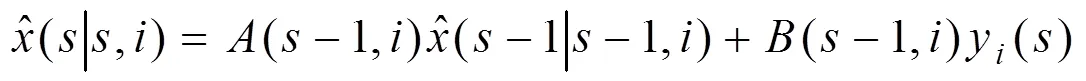
其中：

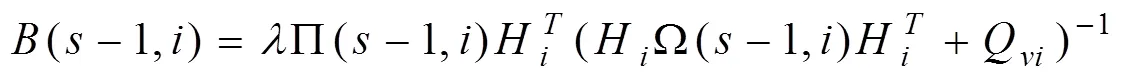
和

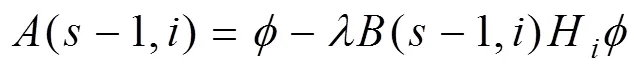
并且：

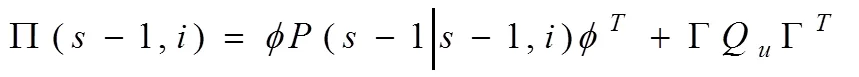
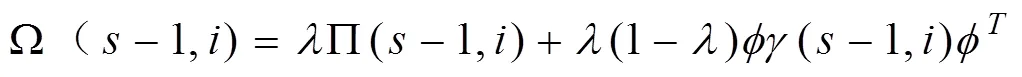
将(1)代入(11)，整理得

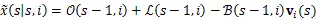
其中

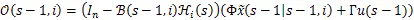
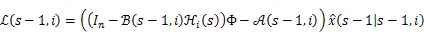
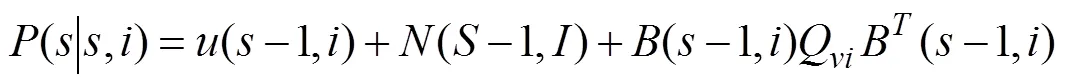
且有Δ(-1,)=-(-1,)H-(-1,)。

对式(13)右边完全平方，利用(10)，得

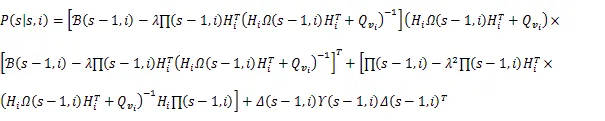
因为式(14)中第二项与(-1,)和(-1,)无关，所以选择(-1,)和(-1,)使上式第一项、第三项为零，从而极小化式(14)，得证式(7)和(8)。

为了计算滤波器，需进一步给出估计误差(|,)的计算。

引理3：估计误差协方差矩阵(|,),k<≤k-1，=+1,…,满足

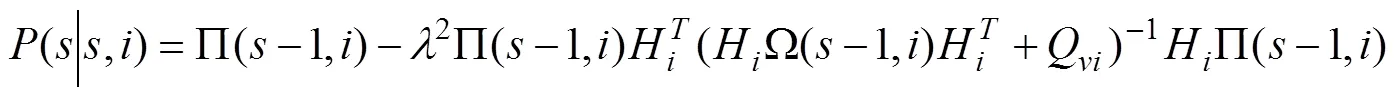
其中初始值为(0|0,+1)=0和(k|k,+1)=(k|k,)，并且P(-1,)和W(-1,)分别由(9)和(10)给出。

证明根据(7)、(8)和(14)，结论易得。

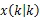
注4：显然，由于时滞的存在，传统的Kalman方法不适合于系统(1)-(2)。利用重组观测和完全平方方法，定理1给出了线性最优滤波器的设计算法。

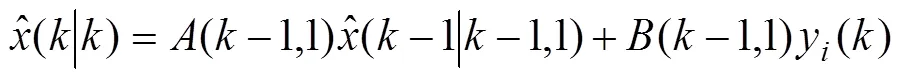
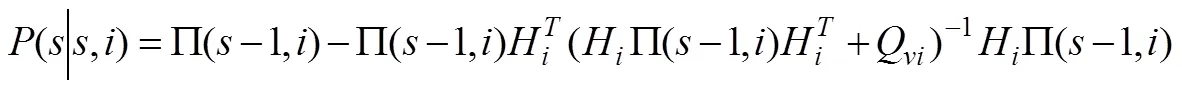
注意到，º1时，原始系统(1)-(2)变成了[11]中考虑的系统模型(2.1)-(2.2)。进一步观察滤波器(17)经过简单的变换即为[11]中所得到的滤波器(3.20)。

3 数值例子

本节给出一个数值例子阐明论文提出方法的有效性。

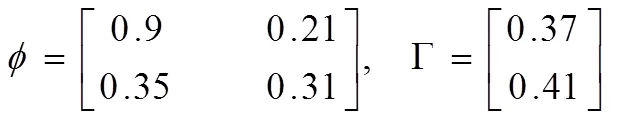
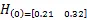
假设噪声(),(0)()和(1)()是互不相关的白噪声，方差为0.3，进一步假设=0.93。 应用MATLAB仿真软件，根据定理1，线性最优滤波器的仿真结果将展示在图1和图2中。可以清晰地看出状态估计曲线能够很好地跟踪原始状态，进一步说明了所提出新算法的有效性。

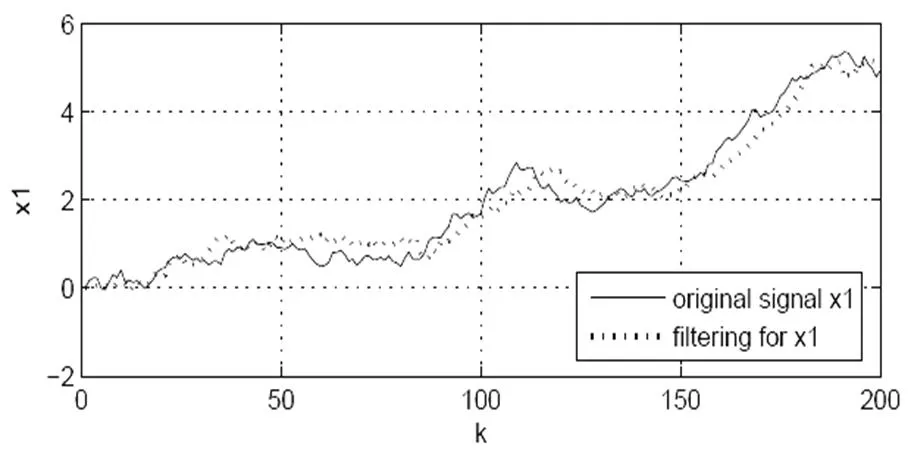
图 1 信号1的滤波器跟踪性能

Fig.1 Filter tracking performance of the signal1

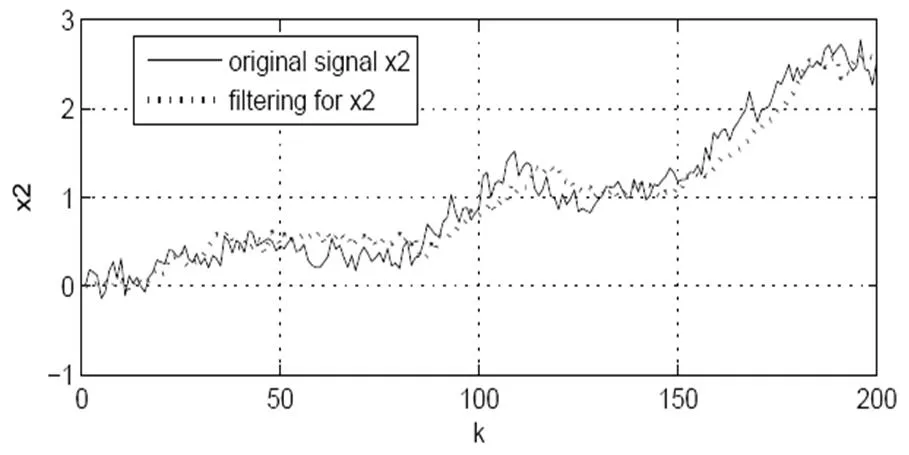
图 2 信号x2的滤波器跟踪性能

4 结语

利用完全平方和重组观测技巧，本文研究了观测中含有不确定参数的线性定常时滞系统的线性最优滤波问题。通过重组观测，使一个时滞滤波问题转化为非时滞滤波问题，进一步应用完全平方技巧，使线性最优滤波器的计算归结为计算+1个与原系统有相同维数的Riccati方程和一个Lyapunov递推等式。该方法无需状态扩维，计算简单。

[1] Kailath T, Sayed AH, Hassibi B. Linear estimation[M]. Englewood Cliffs, NJ: Prentice-Hall, 1999

[2] Zhang H, Xie L. Control and estimation of systems with input/output delays[M]. Heidelberg Berlin: Springer-Verlag, 2007

[3] Fridman E, Shaked U, Xie L. Robust2filtering of linear systems time delays[C]. Nevada,USA: Proc of 41th IEEE Conf. Decision Contr., Las Vegas, 2002:3877-3882

[4] Hou W, Fu M, Zhang H,. Consensus conditions for general second-order multi-agent systems with communication delay[J]. Automatica,2 017,75:293-298

[5] Qiu Z, Liu S, Xie L. Distributed constrained optimal consensus of multi-agent systems[J]. Automatica, 2016,68:209-215

[6] Nahi NE.Optimal recursive estimation with uncertain observation[J]. IEEE Trans.Infor. Theory, 1969,15(4):457-462

[7] Hadidi MT, Schwartz SC. Linear recursive state estimators under uncertain observations[J]. IEEE Trans. Automat. Contr., 1979,24(6):944-948

[8] Hermoso CA, Linares PJ. Linear estimation for discrete-time systems in the presence of correlated disturbances and uncertain observations[J]. IEEE Trans. Automat. Contr., 1994,39(8):1636-1638

[9] Wang F, Balakrishnan V. Robust Kalman filters for linear time-varying systems with stochastic parametric uncertainties[J]. IEEE Trans.Signal Proc., 2002,50(4):803-813

[10] Wang F, Balakrishnan V. Robust steady state filtering for systems with deterministic and stochastic uncertainties[J]. IEEE Trans.Signal Proc., 2003,51(10):2550-2558

[11] Yang Z, Yang C, Deng Z. Guaranteed-cost robust Kalman filters for time-invariant systems with uncertain noise variances[J]. Contral Theory &Applications, 2016,33(4):446-452

[12] Liu W, Wang X, Deng Z. Robust centralized and weighted measurement fusion Kalman estimators for uncertain multisensor systems with linearly correlated white noises[J]. Information Fusion, 2017,35(3):11-25

[13] Hu CB, Ho GQ, Daniel WC,. Distributed robust fusion estimation with application to state monitoring systems[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2017,47(11):2994-3005

[14] Zhao H, Zhang H, Cui P. Steady-state optimal filtering for continuous systems with timedelay[J]. IEEE Signal Proc. Lette., 2009,6(7):628-631

[15] Zhao H, Zhang H, Zhang C,. Optimal filtering for linear discrete-time systems with signal delayed measurement[J]. Inter. Journal of Contr. Auto., 2008,6(3):378-385

[16] Lu X, Zhang H, Wang W,. Kalman filtering for multiple time-delay systems[J]. Automatica, 2005,41(8):1455-1461

[17] Sage AP, Melsa JL. Estimation theory with applications to communications and control[M]. New York: Mcgraw Hill, 1971

Optimal Filtering Wave for Uncertain Linear Time –Delay System

GUO Xiao-chun

271021,

A simple and effective optimal filtering algorithm is proposed for linear uncertain systems with time delay by using recombinant observation analysis and complete square method. First, the time-delay filtering problem is transformed into a non-time-delay problem, then the design of the filter is given by solving the Lyapunov equation and the+1 Riccati matrix equation with the same dimension as the original system, and finally, the correctness and the effectiveness of the algorithm are explained by a simulation example.

Time-delay system; Linear; filtering wave

[TP13]

A

1000-2324(2019)04-0656-05

2018-1-18

2018-6-20

郭小春(1973-),女,硕士,高级实验师,主要研究方向为时滞系统控制. E-mail:gxc99gxc@126.com