马登理论在排列组合教学中的应用与启示

(浙江师范大学附属萧山二中,浙江 杭州 311251)(浙江师范大学教师教育学院,浙江 金华 321004)

“现象图式学”是由瑞典教育家马登所发展起来的一个教学理论，也被称为“马登理论”．其中，鉴别和差异是该理论的核心内容，马登借助这两个核心概念提出了一些学习活动的新见解．

第一，学习是一种鉴别.马登指出，学习认识事物或者现象就是从对象中区分出一些主要特征，并将注意力集中于这些共性．这就要求教师在平时的教学中，多给学生创设不同的情景，鼓励学生将陌生的学习对象转化成自己熟悉的知识，将新的问题套用已有的模型进行处理，从而提高解决复杂数学问题的能力．

第二，差异可以是变异．与题海战术相比，教师在教学中应该更加关注练习所包含的变异性，因为学生能够体验到的关于学习对象的各个方面越多，他能够进行的学习空间就越大．如何使有效的变异发生？这就要求教师平时有意识地对数学问题进行积累、归类以及变式研究，同时在课堂上多提供一些差异性的情景和不同角度、维度的变式练习．

笔者从上述两个方面结合高中数学排列组合中的几个案例，谈谈自己的看法，望有助于促进课堂教学的有效性．

1 排列组合问题的变式探究

著名的数学家波利亚认为：“一个有责任心的教师与其穷于应付繁琐的数学内容和过量的题目，还不如适当地选择某一些有意义但又不太复杂的题目，去帮助学生发掘题目的各个方面，在指导学生解题的过程中，提高他们的才智和推理能力．”[1]根据这一想法，教师应注重在练习题的变化和区分中，不断促进学生从表层学习向深层学习的进化．

而练习题的变式应侧重两个方面：一方面，对于同一问题的“垂直变式”，教师应准确拿捏“渐变”的力度，从容易理解的角度出发，逐渐增加题目的难度和认知的负荷，在学生的“最近发展区”内使学生的思维得到延展，同时促进学生鉴别问题和解决问题的能力进一步提升；另一方面，对于看着相似但解题方法和思路却截然不同的“水平变式”，教师可以多设置类似的问题，在指导学生解题的过程中培养他们的思辩能力，让学生在相同情景下体验不同的数学思维，帮助他们发掘题目的各个方面．

例16个不同的球，全部放入3个编号分别为1,2,3的盒子中．

1)任意放，有多少种放法？

2)3个盒子中的球数分别为1,2,3，有多少种放法？

3)每个盒子中至少有一个球，有多少种放法？

4)恰有一个盒子为空，有多少种放法？

5)每个盒子中的球数和编号一致，有多少种放法？

分析1)每个元素都有3个位置可供选择，因此N=36.

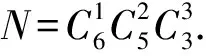
该例的5个小问题就是典型的“垂直变式”，从乘法计数原理的相关问题出发再到一般的分组问题、平均分组问题、定序问题，由一般到特殊，层层递进，从而引导学生对这一系列问题有一个全面而深刻的认识．教师在设计这一系列问题之时要注意逐步体现问题的难度和深度．课前准备时要反复琢磨自己设定的这些问题是否构成一个环环相扣的体系，是否能够引导学生积极思考，是否能锻炼学生面对复杂问题应具备的能力．

例26个相同的球，全部放入3个编号分别为1,2,3的盒子中．

1)每个盒子中的球数和编号一致，有多少种放法？

2)恰好有两个盒子为空，有多少种放法？

3)恰有一个盒子是空盒，有多少种放法？

4)每个盒子中至少有一个球，有多少种放法？

5)任意放，有多少种放法？

分析1)因为是相同的球，所以分成1,2,3这样的3堆只有一种分配的方法．又要与盒子上的编号一致，故只有一种放法，即N=1．

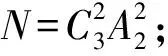
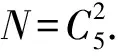
5)方法1分类讨论的情况即为第2)～4)小题的情况，相加即可．

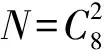
例2是例1的变式，小球由“不同”变成“相同”之后，解题的思路和方法发生了改变，这就是“水平变式”．教师可以根据例1的解题思路，引导学生用类似分类讨论的方法来解决例2的相关问题，然后再来探索更为简洁的“隔板法”．例1和例2中小题放置的顺序发生了一些变化，例1中的小题按照从一般到特殊排序，体现了学生思维的发展过程；例2中则是由特殊到一般，符合题目难度从浅到深、学生认知负荷逐渐增加的特征．教师在上课过程中应积极主动地触发“有效的变式”，使得课堂环环相扣、难度层层递进，让学生在不断思考差异的过程中获得解题能力和思维逻辑．

2 排列组合问题的鉴别探究

人对于问题的解决，往往首先思考的是头脑中的固有经验和模型，一旦找到了这样能套用的模式，就能迅速找到解决问题的方法，这就是“鉴别”[2]．排列组合中的题目类型丰富，看似千变万化，但实际上很多问题都是固定模型在不同背景或者不同实际情况下的实践和运用．比起传统的题海战术，教会学生思考如何在各种问题情境下鉴别出已知模型，更能帮助学生提高解题速度和正确率．

例3完成以下小题:

1) 9个名额分给6所学校，每个学校至少一个名额，共有______种分法;

2)从5个学校中选出8名学生组成代表团，要求每个学校至少有1人，共有______种分法;

3)方程x+y+z=8有______组不同的正整数解.

例4完成以下小题：

1)有5本不同的书，把它们全部送给3个学生，每人至少一本，有______种不同的送书方法；

2) 3人参加5个不同的游戏，每个游戏最多2人参加(如果2人同时参加一个游戏，不区分2人在其中的角色)，则不同的参与方式共有______种；

3)红、黄、绿3种颜色的卡片分别标有字母A,B,C,D,E各一张，每次取出5张，要求字母各不相同，3种颜色齐全的取法有______种.

正是有了这种学习模型的鉴别，在解决具体排列组合的问题中，才能发现许多问题其实可以抽象成“a个不同的球放入b个不同盒子”或者“a个相同的球放入b个不同盒子”这两个模型，前者可以通过先分堆再分配的思路解题，后者可以用隔板法解决．学生需要在解题过程中不断鉴别出这样的模型，这就是马登理论所说:学习是一种鉴别.

对于教师的课堂教学而言，也应该积极提倡一法多用．同一种方法只有不断地应用于各种问题情境，才能使学生认识不同问题情境中问题解决的方法的同一性，进而掌握该方法的实质[3]．这就要求我们在实际教学中创设不同特质、不同类型、不同背景的题目，为学生营造出一法多用、鉴别模型的学习条件．作为一名数学教师，不能只刻板地、离散地传授学生解题方法，而是要有导向性地创设变式情景、强化方法形成的过程、围绕核心问题剖析重难点，教会学生如何学习、如何思考、如何系统地将知识点联系起来．

马登理论整个理论都围绕着一个教学目的，就是更好地发展学生．着眼于当下，是为了学生更好地提高学习的效率和质量；放眼于未来，是为了学生更快地适应社会的变化．马登理论作为一个深层次的教学教育理论，笔者仅仅通过排列组合这块知识展现了它最浅层的两个含义．实际上，它的理念非常符合高中数学核心素养发展的需要，值得我们进一步探讨和深思．