数学思维空间成就数学思维品质
——对2018年浙江省台州市中考数学试题第16题的思考

王国顺

一年一度的中考已经落下帷幕，在以能力立意，培养学生数学核心素养的今天，今年浙江省台州市卷的第16题（填空题）重在考察学生数学知识的整合能力、探索解题过程的思维品质，为初中数学教学起到了很好的导向作用。可以说此题是简约而不简单，更是一道考查学生数学思维能力与思维品质的好题。因此，笔者以此题为例，进行了思考与探索，和各位专家、同仁一起探讨。

一、原题呈现

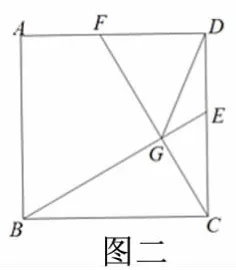
【例1】如图1，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为______。（2018浙江省台州市中考数学试题第16题）

二、思路剖析

一方面，根据CE=DF，在正方形中，因为BC=CD，∠BCE=∠CDF=90°∴△BCE≌△DCF，

∴∠CBE=∠DCF ∵∠DCF＋∠BCF=∠BCD=90o

∴∠CBE＋∠BCF=90°，∴∠BGC=90°（即BE⊥CF）

∴△BCG是直角三角形。题目中的隐含条件被进一步挖掘，并凸显出来。在直角三角形中，要确定边与边的关系，自然而然会联想到勾股定理，不妨设CG=x，BG=y，则x2＋y2=32。

另一方面，题中的面积关系也是思考的方向，我们研究的重点是△BCG，根据“图中阴影部分的面积与正方形ABCD的面积之比为2：3”，转化为“图中空白部分的面积与正方形ABCD的面积之比为1：3”，

∵△BCE≌△DCF ∴S△BCE=S△CDF，

∴S△BCE-S△CEG=S△CDF-S△CEG，∴S△BCG=S四边形EDFG，

∴S△BCG=

这时只要运用整体思想，求出（x＋y）的值即可。而

（x＋y）2=x2＋y2＋2xy=9＋6=15，

笔者分析学生可能受到习惯性思维的干扰，一心只想精准求出两直角边的值，把y=）2=9，方程化为x4-9x2＋9=0，先把x2看成整体，设x2=a，方程化为关于a的一元二次方程a2-9a＋9=0，解得a=，那么x2=或x2=∵x＞0，∴x1=或x2=，

代入x2＋y2=9得x2＋（

相应地y1=或y2=

由于学生所学知识的局限性，导致含双重根号的结果无法化简，除非你平时接触到过利用配方法化简这一类特殊形式二次根式，例如，x1

这些同学思维不可谓不缜密、计算能力不可谓不强，可结果正确与否的担忧却无法消除。为什么会在考试的时候出现这种既浪费时间又繁琐易错的思路呢？问题的根本在于平时的训练过于机械，思路单一、缺少发散性，导致在紧张的考试中思维品质不升反降。“解题时迈进的每一步，如果越来越简单，你会感到路走对了，胜利就在前头，如果越来越复杂，越来越艰难，你也应该发现前景不妙，希望渺茫，简单自然，往往是你判断的标准。”［1］

三、引发的思考

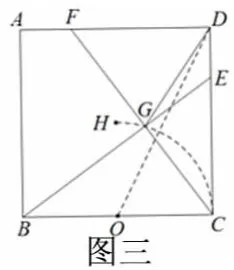
1.良好思维品质的形成，需要学生“见多识广”良好的数学思维品质的形成，首先需要老师在平时的教学活动中多关注、狠落实，只有经常接触举一反三、一题多解、多题归一的教学，才能够在单打独斗时，妙想绝处生捷径自然成.例如“变式1”，我们可以将刚才的静态问题升华为动态问题进行变式探索，使学生的思维活动在不同的方向和不同的层次上得到发展.【变式1】如图2，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G，连接DG.在点E从C运动到D的过程中，求①点G 运动的路径长为__________；②DG的最小值为；__________；③当DG=DF时，CE的值__________.

分析与解：由原题的剖析知道，在点E从C运动到D的过程中，△BCG是始终是以BC为斜边的直角三角形，因此，点G在以BC为直径的圆（如图3，圆心记为O）上运动，它的路径是一段圆弧（四分之一个圆），第①问解决；在①的基础上，当D，G，O共线时，DG最小，DG最小值=；对于问题③，只有当∠DFG=∠FGD时，DG=DF∵AD∥BC∴∠DFG=∠OCG，

根据OG=OC，∠OGC=∠OCG，当D，G，O共线时，∠OGC=∠FGD

∴∠DFG=∠FGD∴DF=DG，又∵CE=DF，即CE=

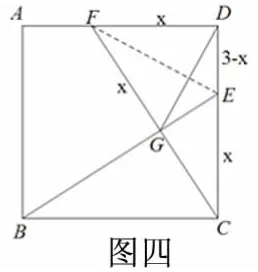
这里为什么不把③设置为“当△DFG为等腰三角形时，求CE的值”这样的开放式的问题呢？解决时要进行分类讨论，不是更能够锻炼学生的思维能力吗？是的，刚刚的CE=是情形之一，另一种情形就是当G与H重合时，GD=GF，此时CE=CD=3；情形三，DF=FG时，如图4，连接EF，则Rt△BCE≌Rt△DCF，

∴GE=DE，设CE=DF=FG=x，∴GE=DE=3-x，

化为整式方程得，2x3-6x2＋18x-27=0，不是特殊形式一元三次方程，初等数学无法解决（需要用高等数学“卡尔丹公式法”或“盛金公式法”求解，它的实数解约为1.94）。因此，作为思维训练，培养探究能力，也未尝不可，但作为考试题，我们在设计的时候必须要规避。

2.良好的数学思维品质的形成，需要教师“精心编导”举一反三、一题多解、一题多变能够有效的锻炼学生的数学思维能力和品质，类比学习对锻炼学生的数学思维是非常有效的，类比对知识的全面掌握与方法的迁移、能力的提升，都有十分重要的作用。“素材选用不仅有利于学生理解所学知识的内涵，还能够更好地揭示相关数学知识之间的内在关联，有利于学生从整体上理解数学，构建数学认知结构。”［3］如下面的变式2，就是从考查学生综合运用数学的能力方面进行构建，以激发学生的分散性思维。

【变式2】如图5，在正方形ABCD中，AB=3，点E在CD上，F在AD上，FE⊥BE，M是EF的中点，MH⊥CD。在点E从C运动到D的过程中，线段MH的最大值为__________。

分析与解：易得MH是△DEF的中位线，要使MH最大，只要DF最大，这里∠C=∠FEB=∠D=90°，那么∠CBE=∠DEF，∴Rt△BCE∽Rt△EDF，∴，设CE=x，DF=y，则DE=3-x，，y=＋x，即y=，

正如陈永明教授在“习题教学的归一原则”中所指出的——“多解归一、多题归一、举一反三，就是要找同类问题的共同点，把共同的经验总结出来，以便运用到新的场合”。［2］在变式2中，我们改变了原题中的条件，解决问题的方法就从原来的两个三角形全等迁移到两个三角形相似，利用相似比，得到二次函数，并用二次函数的性质求最大值，知识都是初中数学体系中的核心知识。

四、结语

学生良好的数学思维品质、数学核心素养的形成应该是渐进的、逐步累积的结果，绝不是一蹴而就的。教师只有在平时的教学活动中多展现锻炼数学思维的课例、多渗透思考问题的方法与步骤、使学生能够会知识迁移和方法类比，学生心里才能埋下形成良好数学思维品质的种子，数学课堂必定大放异彩，成效更显著，正如史宁中教授所说“用数学的眼光看世界，用数学的思维分析世界，用数学的语言表达世界”的核心素养必能得到极大提升。