Dynamics of the Moving Ring Load Acting in the System“Hollow Cylinder + Surrounding Medium” with Inhomogeneous Initial Stresses

Surkay D.Akbarov,Emin T.Bagirov and Muslum Ozisik

Abstract:This paper studies the influence of the inhomogeneous initial stress state in the system consisting of a hollow cylinder and surrounding elastic medium on the dynamics of the moving ring load acting in the interior of the cylinder.It is assumed that in the initial state the system is compressed by uniformly distributed normal forces acting at infinity in the radial inward direction and as a result of this compression the inhomogeneous initial stresses appear in the system.After appearance of the initial stresses,the interior of the hollow cylinder is loaded by the moving ring load and so it is required to study the influence of the indicated inhomogeneous initial stresses on the dynamics of this moving load.This influence is studied with utilizing the so-called threedimensional linearized theory of elastic waves in elastic bodies with initial stresses.For solution of the corresponding mathematical problems,the discrete-analytical solution method is employed and the approximate analytical solution of these equations is achieved.Numerical results obtained within this method and related to the influence of the inhomogeneous initial stresses on the critical velocity of the moving load and on the response of the interface stresses to this load are presented and discussed.In particular,it is established that the initial inhomogeneous initial stresses appearing as a result of the action of the aforementioned compressional forces cause to increase the values of the critical velocity of the moving load.

Keywords:Inhomogeneous initial stresses,dynamics of a moving load,critical velocity,hollow cylinder,elastic medium,ring load.

1 Introduction

A more detailed and fundamental study of the dynamic problems related to underground structures which,as usual,are modelled as a hollow cylinder (see,for instance[Abdulkadirov (1981);Hasheminejad and Komeili (2009)] and others listed therein)or beam (see,for instance [Czyczula,Koziol,Kudla et al.(2017);Ding,Zhu,Luo et al.(2016)]and others listed therein)surrounded with an elastic medium,requires the reference particularities of these structures to be taken into consideration,one of which is the inhomogeneous initial stresses which appear as a result of the earth’s gravity.A priori,it should be noted that the effect of the noted reference particularity on the dynamics of the underground structures cannot be modelled within the scope of classical linear elastodynamics,however,such an effect can be modelled within the framework of the three-dimensional linearized theory of elastic waves in bodies with initial stresses.It should also be noted that up to now such investigations,i.e.,investigations carried out within the scope of the three-dimensional linearized approach which take into consideration the inhomogeneous initial stresses,are almost completely absent.Nevertheless,the investigations which relate to the corresponding stability loss problems of mine workings have been carried out by Guz [Guz (1977)] and a review of these investigations is given in the paper by Guz [Guz (2003)].However,in these investigations,the mine workings are modelled as an infinite homogeneous elastic or elastoplastic medium containing a cylindrical cavity and the variational method is employed for the solution to the corresponding eigenvalue problems.

There are also a few investigations carried out by Engin et al.[Engin and Suhubi (1978);Shearer,Abrahams,Parnell et al.(2013);Wu,Su,Liu et al.(2018)] and Akbarov et al.[Akbarov and Bagirov (2019)] related to wave dispersion in hollow and compound hollow cylinders with inhomogeneous initial stresses caused by internal and external hydrostatic pressures.

Before the formulation of the subject of the present paper,we consider a brief review of the investigations related to the dynamics of the system “hollow cylinder + surrounding elastic medium” carried out up to now.First of all,we note that such investigations are made mainly,as indicated above,in the framework of classical linear elastodynamics and the main significant results are obtained in the works by Pozhuev et al.[Pozhuev (1980);Abdulkadirov (1981);Chonan (1981);Hasheminejad and Komeli (2009);Hussein,François,Schevenels et al.(2014);Yuan,Bostrom and Cai (2017)] and others listed therein.Here,we briefly consider some of them and begin with the paper by Chonan[Chonan (1981)] in which the dynamic response of a cylindrical shell surrounded by an infinite elastic continuum to the axisymmetric ring pressure which acts in the interior of the shell and moves with constant velocity,is studied.Note that under this study,the thick shell theory is employed for describing the motion of the shell,however,the motion of the surrounding elastic medium is written by the exact equations of linear elastodynamics.At the same time,it is assumed that the cylindrical shell and surrounding elastic medium are joined to each other through a thin elastic bond.Within the scope of the foregoing assumptions,the numerical results on the critical velocity of the moving load and on the radial displacement of the shell are presented and discussed.

The moving ring load problem for the system consisting of the cylindrical thin shell and surrounding infinite elastic medium is also studied in the paper by Pozhuev[Pozhuev (1980)],however,in that paper it is assumed that the material of the surrounding medium is transversally isotropic,the symmetry axis of which is parallel of the central axis of the cylindrical shell.Numerical results regarding the displacements and a radial normal stress are presented but numerical results related to the critical velocity of the moving load are not presented.

The paper by Abdulkadirov [Abdulkadirov (1981)] also studies the critical velocity of the moving ring load acting in the interior of the hollow cylinder surrounded by an infinite elastic medium.Unlike the foregoing papers by Chonan et al.[Chonan (1981);Pozhuev(1980)],in the paper by Abdulkadirov [Abdulkadirov (1981)],not only the motion of the surrounding elastic medium but also the motion of the cylinder is described by the exact equations of elastodynamics and the critical velocity is determined from the dispersion curves of the corresponding waves propagating in the system under consideration.

The case where the hollow cylinder is embedded in the fluid-saturated infinite poroelastic medium and where the moving ring load acts in the interior of this cylinder,is considered in the paper by Hasheminejad et al.[Hasheminejad and Komeli (2009)].For describing of the motion of the fluid-saturated permeable medium,Biot’s dynamic theory of poroelasticity is employed.It is assumed that the cylinder and fluid-saturated medium are connected through the thin massless viscoelastic bond and the difference between the radial and axial displacements of the cylinder and porous medium are expressed through the corresponding stresses acting on the interface.More precisely,the (a1+a2∂∂t)type differential operator is used (wherea1anda2are constants andtis the time)in order to express the stresses through the displacements' discontinuities across the interface surface.Numerical results are presented for the radial displacements of the shell’s wall and of the porous soil on the interface points and the focus is on the influence of the foregoinga1anda2constants on these displacements.

In the papers by Hussein et al.[Hussein,François,Schevenels et al.(2014);Yuan,Bostrom and Cai (2017)] and others listed therein,mathematical methods are developed for a solution to the more complicated problems related to the moving load dynamics acting in the interior of the hollow cylinder embedded in infinite layered [Hussein,François,Schevenels et al.(2014)] and semi-infinite homogeneous elastic mediums[Pozhuev (1980)].However,in these works,only the vibration of the surrounding mediums caused by the moving load are analyzed.

In the last four years,a series works has been published by the first author of the present paper and his students (see,for instance the papers by Akbarov et al.[Akbarov and Mehdiyev (2018a,2018b);Ozisik,Mehdiyev and Akbarov (2018)] and others listed therein)which also relate to the dynamics of the moving load acting in the interior of the hollow cylinder surrounded with elastic medium.Note that in these works,the investigations are made by utilizing the exact equations of elastodynamics for describing not only the motion of the infinite surrounding elastic medium but also the motion of the hollow cylinder.At the same time,in these works,not only are the dynamics of the load which moves with constant velocity considered,but also the dynamics of the oscillating moving load [Akbarov and Mehdiyev (2018b)].Moreover,in these works not only the axisymmetric problems have been considered,but also the three-dimensional nonaxisymmetric problems [Akbarov and Mehdiyev (2018b)].Numerical results on the influence of the problem parameters on the critical velocity of the moving load and on the interface stresses are presented and discussed.

With these we restrict ourselves to consideration of the review of the investigations regarding the dynamics of the moving load acting in the interior of the hollow cylinder surrounded with elastic medium.According to this review,it can be concluded that in all these reviewed works one of the main factors which is characteristic for underground structures is that the inhomogeneous initial stresses which appear as a result of the earth’s gravity are not taken into consideration.

Thus,taking the foregoing statement into consideration in the present paper,the attempt is made for investigation of the dynamics of the moving ring load acting in the interior of the cylinder surrounded with an elastic medium in the case where the cylinder and surrounding elastic medium have inhomogeneous initial stresses caused by uniformly distributed compressional forces acting at infinity in the inward radial direction.

Finally,we note that in the paper by Akbarov et al.[Akbarov and Mehdiyev (2018a)],the dynamics of the moving ring load problem is also considered for the initially stretched or compressed “cylinder + surrounding medium” system.However,in the case considered in the paper by Akbarov et al.[Akbarov and Mehdiyev (2018a)],the initial stresses are taken as homogeneous ones and it is assumed that these stresses are caused by uniaxial compression or stretching of this system along the cylinder’s axis.

2 Formulation of the problem

Consider the system consisting of the hollow cylinder with thicknesshand surrounding elastic medium,the sketch of which is shown in Fig.1.Assume that the external radius of the cross section of the cylinder isRand the materials of the constituents of the system are homogeneous and isotropic.Moreover,assume that in the initial state (i.e.,before the action of the moving ring load in the interior of the cylinder),the system under consideration is compressed by a uniformly distributed force with intensityqacting at infinity in the inward radial direction,and these forces cause the inhomogeneous stress state which is called the initial stress state.Note that such initial loading can be taken as modelling of the appearing of the stress state in underground structures as a result of the earth’s gravity.

We associate the CartesianOx1x2x3and cylindricalOrθ zcoordinate systems Fig.1 with the central axis of the cylinder and the position of the points of the constituents are determined with the Lagrange coordinates.

Below,the values related to the cylinder (to the surrounding medium)will be indicated with the upper index (2)(upper index (1))and the values related to the initial stresses will be differentiated by the additional upper index 0.

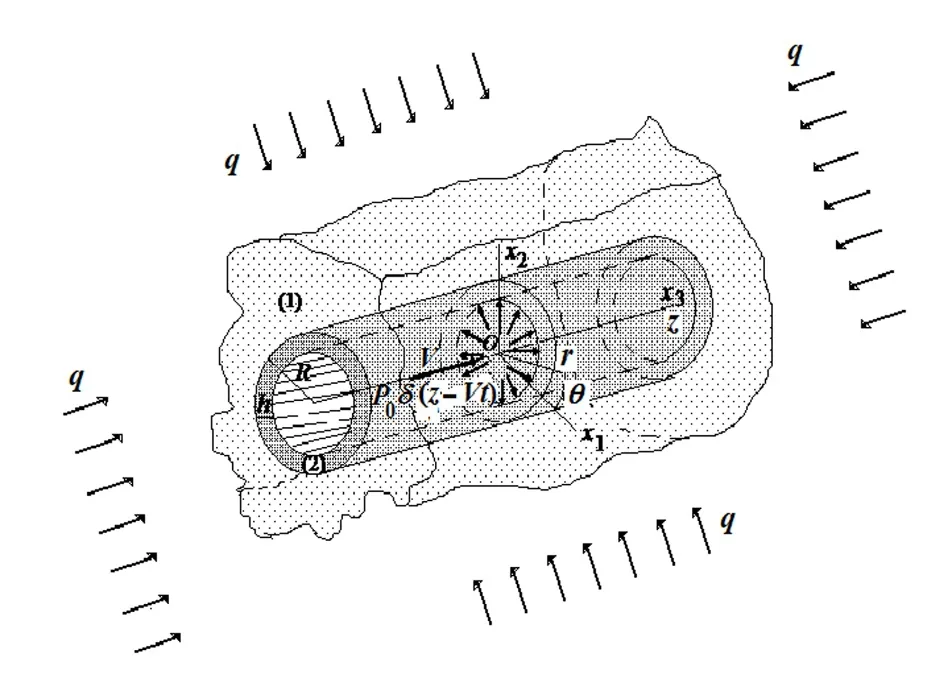
Figure1:Sketch of the “hollow cylinder+surrounding elastic medium” system

We use the classical linear theory of elasticity for determination of the initial static stresses caused by the uniformly distributed compressional forces with intensityqwhich act at infinity in the inward radial direction.Herein,we write the expressions for the initial stresses without any details as the solution procedure can be found in many monographs and textbooks regarding the classical linear theory of elasticity.Thus,these expressions are the following ones.

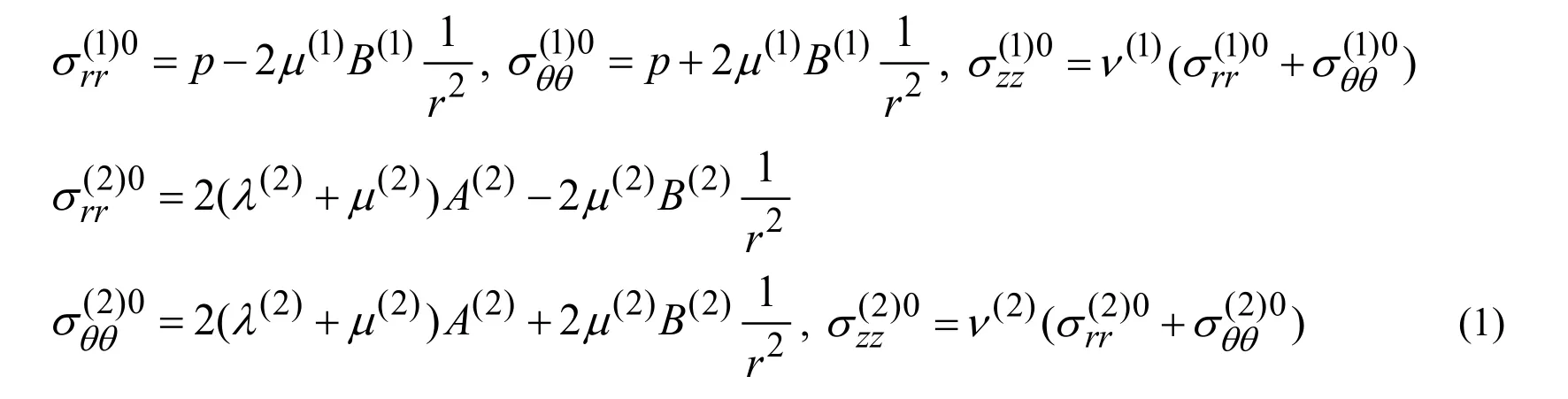
In (1),λ(n)andµ(n)are the Lame constants andν(n)is Poisson’s ratio of then-thmaterial and the unknown constantsB(1),A(2)andB(2)are determined from the following equations：

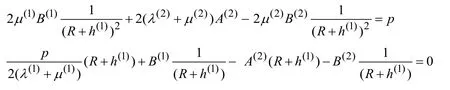
which are obtained from the corresponding boundary and contact conditions satisfied under determination of the initial stresses.

Thus,through the expressions in (1)and (2),the initial stresses in the system under consideration are determined and it is required to investigate how these initial stresses affect the dynamics of the moving ring load (i.e.,on the values of the critical velocity of this load,on the values of the interface stresses,etc.)in the interior of the cylinder surrounded with an infinite elastic medium.To carry out this investigation,we must use the 3D linearized theory of elastic waves in bodies with inhomogeneous initial stresses,the equations and relations of which are given in the monographs by Guz et al.[Guz(2004);Eringen and Suhubi (1975);Akbarov (2015)] and in others listed therein.In the case under consideration,i.e.,in the axisymmetric case,these equations and relations can be written as follows.

The equations of motion：

where

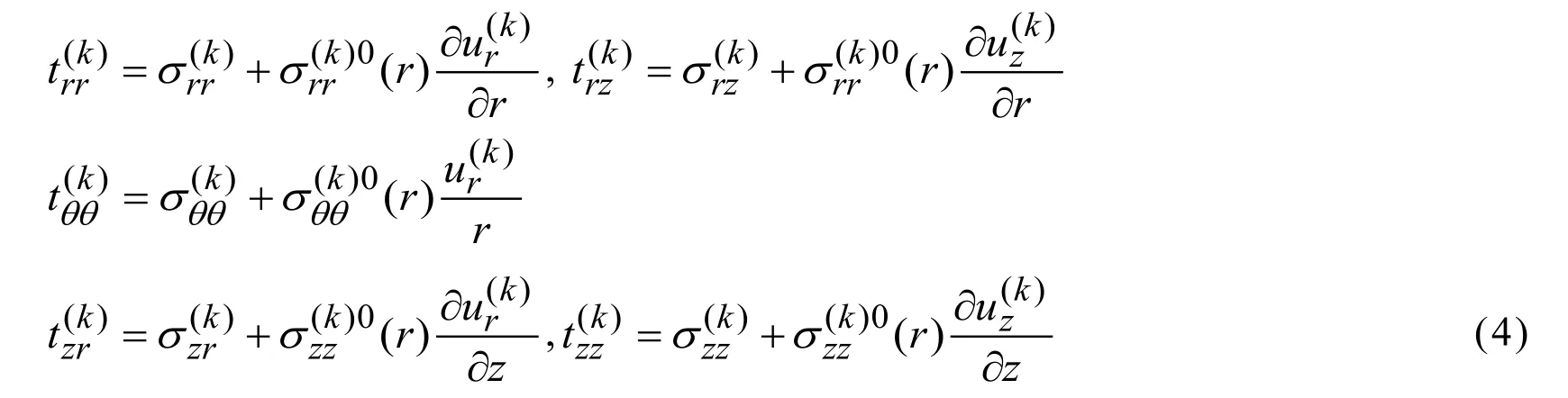
The elasticity and strain-displacement relations：

Now we formulate the corresponding boundary and contact conditions.According to Fig.1,we can write the following conditions in the interior of the hollow cylinder and the decay conditions for the quantities related to the surrounding elastic medium.

In (7),Vindicates the velocity of the moving ring load.We assume that on the interface between the cylinder and the surrounding elastic medium,complete contact conditions are satisfied,i.e.,we assume that

Thus,the investigation of the influence of the inhomogeneous initial stresses determined with the expressions in (1)and (2)in the system consisting of the hollow cylinder and surrounding elastic medium on the dynamics of the moving ring load acting in the interior of this cylinder is reduced to the solution of the system of Eqs.(3)-(6)within the scope of the boundary conditions (7)and (8)and the contact conditions in (9).

This completes the formulation of the problem.

3 Method of solution

3.1 Employing the moving coordinate system and the Fourier transforms

First of all,we note that for the solution to the considered problem we will use the classical Lame decomposition (see,for instance,the monograph by Eringen et al.[Eringen and Suhubi (1975)] which for the case under consideration (i.e.,for the axisymmetric case)can be presented as follows.

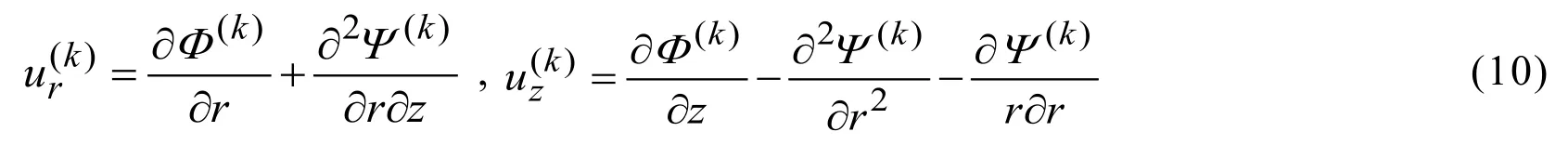
Substituting expressions in (10)into the expressions (6),(5)and (4)and doing some cumbersome mathematical manipulations we obtain the following equations for the potentialsandfrom the equations in (3).

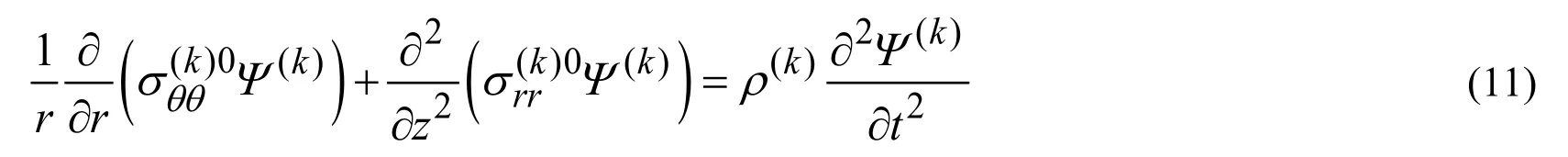
Note that in the case where the initial stresses are absent,i.e.,in the case wherethe equations in (11)coincide with the corresponding ones in classical linear elastodynamics (see,for instance the monograph by Eringen et al.[Eringen and Suhubi (1975)]).

Thus,adding the equations in (11)to the foregoing complete system of Eqs.(3)-(6),we proceed to the solution of these equations with the use of the moving coordinate systemO'r'θ'z'determined with the relations

Note that after application of the coordinate transformation in (12)to the foregoing equations it is found that these equations remain valid as are,taking into consideration the replacement of the operatorwith the operator

Further,we will omit the upper prime over the coordinates and apply the Fourier transform with respect to the coordinatezto all the foregoing equations and relations.Taking into consideration the symmetry and asymmetry of the sought values with respect to the pointz=0the originals of these values can be presented by the following improper integrals.

wheresis the Fourier transform parameter and the lower indexFindicates the Fourier transform of the same-named quantities.

Substituting the expressions (13)into Eqs.(3)-(6),we obtain the complete system of equations with respect to the Fourier transforms of the sought values.This system of equations can be presented as follows which are obtained from the Eqs.(3)-(6).

Note that the first boundary condition in (7)is transformed to the following one

However,the other conditions in (7),(8)and (9)remain valid for their Fourier transforms.Moreover,substituting the expressions in (13)into the Eqs.(10)and (11),we obtain the following equations for the Fourier transforms of the potentials

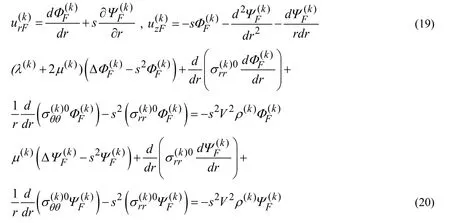
Thus,determination of the Fourier transforms of the sought values are reduced to the solution of the equations in (20).Due to the expressions in (1)and (2),it is evident that it is impossible to find the analytical solution of the equations in (20)and therefore,we attempt to use the discrete-analytical method which allows us to obtain approximate analytical expressions of the sought values.

Note that under application of this method,the solution domain with respect to the radial coordinateris divided into a certain number of subdomains (sub-cylindrical layers)within each of which the initial stresses given through the expressions in (1)and (2)are taken as constant,and the values of these constants are determined through the expressions (1)and (2)by replacing the variablerwithrmwhich is the middle radius of the subdomain’s (or sublayer’s)cross-section.After this procedure,attempts are made to obtain an analytical solution to the system of Eqs.(14)-(17).

Thus,we realize the above-described procedure step by step.

3.2 Dividing regions into a certain number of sub-regions,and contact conditions between these sub-regions

We divide the region [R-h,R]which is occupied with the hollow cylinder into theN2number of sub-regions [R-h+ (n2-1)h/N2),(R-h+n2h/N2)],wheren2=1,2,...,N2.Moreover,we divide the region[R,∞]occupied by the surrounding elastic medium into theN1number of finite sub-regions [R+ (RM-R)(n1-1)/N1,R+ (RM-R)n1/N1]and infinite sub-region [RM,∞],wheren1=1,2,...,N1,and the numbersN2andN1and the value forRMare determined in the solution procedure from the convergence requirement of the numerical results.

Thus,using the foregoing discretization it can be assumed that the inhomogeneous initial stresses determined through the expressions (1)and (2)can be taken as constant within each sub-region,and the values of these constants can be determined through the following expressions.

In then2-thsub-region occupied by the hollow cylinder

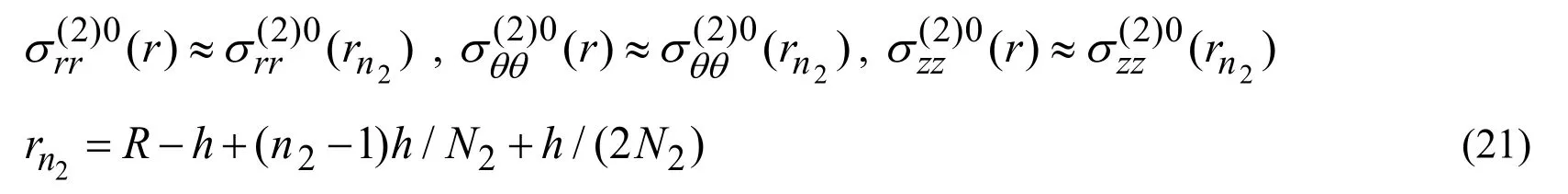
In then1 -thfinite sub-region occupied by the surrounding medium

and in the infinite sub-region [RM,∞]also occupied by the surrounding medium

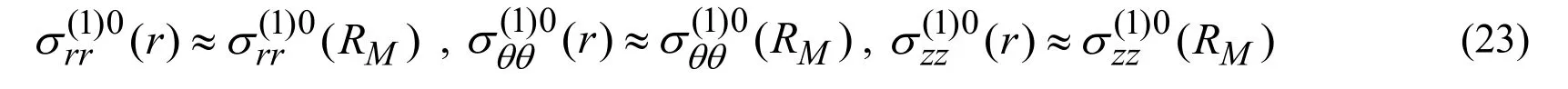
Denoting the values related to the hollow cylinder (surrounding medium)by the upper index (2)n2(by the upper index (1)n1),as well denoting the values related to the infinite sub-region [RM,∞]by the upper index (1)∞we can write from (8),(9)and (18)the following boundary and contact conditions between the sub-regions.

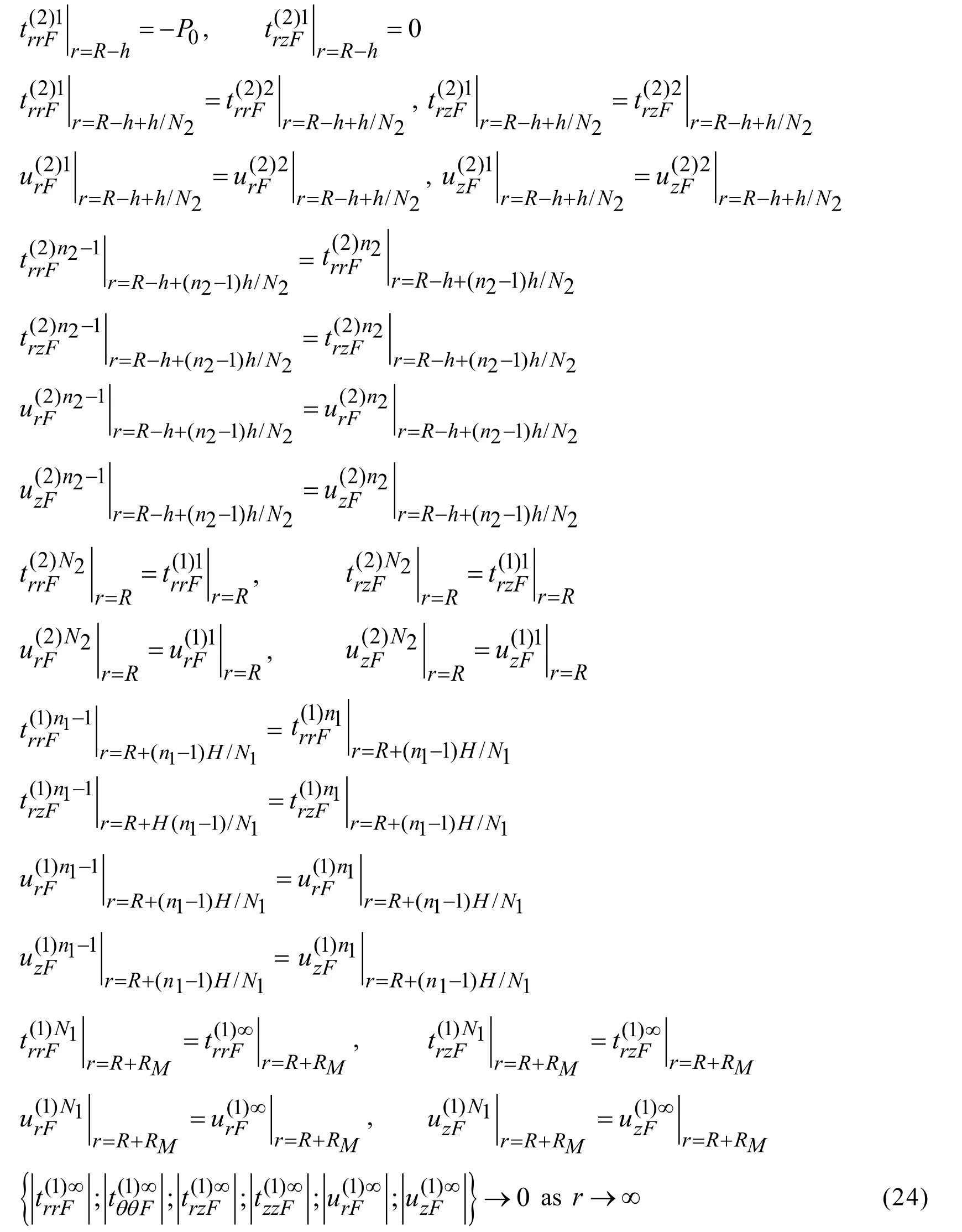
whereH=RM-R

This completes consideration of the discretization of the solution domain and the formulation of the contact conditions between the subdomains.

3.3 Solution procedure to the system of equations (14),(15)and (20)within each subdomain

First of all,note that the relations (16)and (17)remain valid in each subdomain as are,and during the mathematical transformations the upper indices (1)n1,(2)n2and (1)∞must be used instead of the upper indices (1)and (2).

Thus,taking into account (21),(22)and (23),the equations given below are obtained from Eqs.(14)and (15).

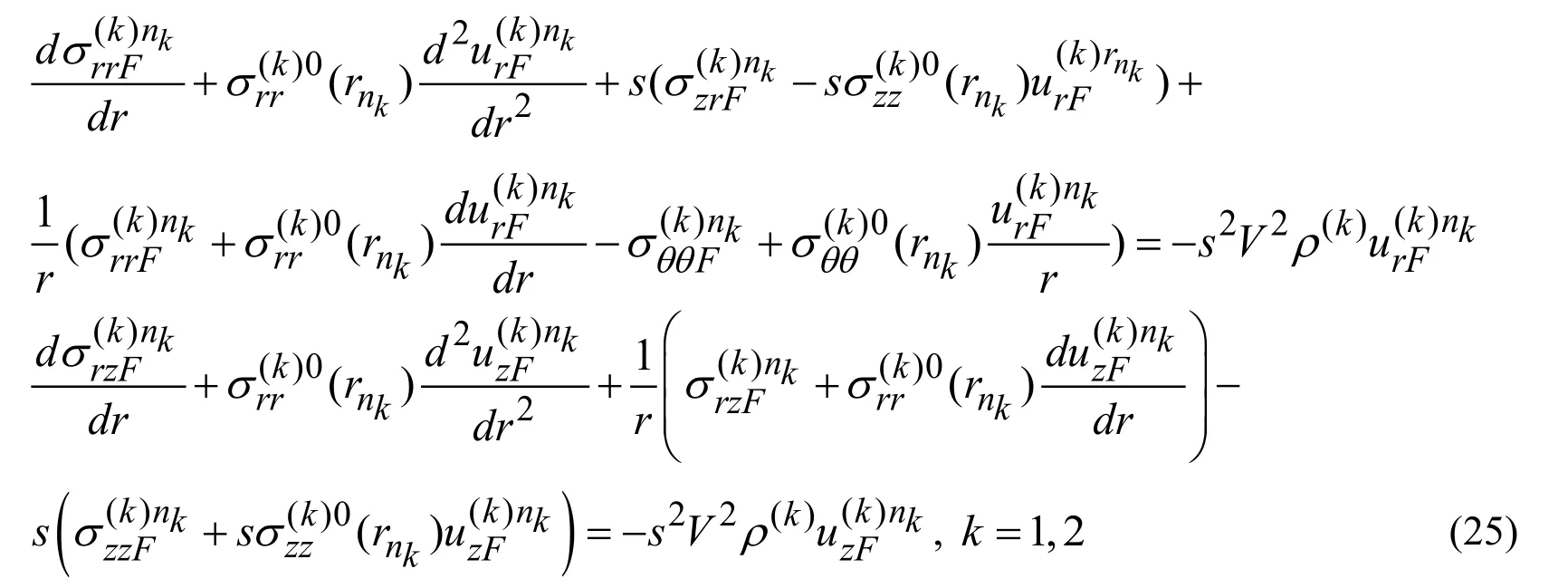
It is evident that by writing the upper index (1)∞instead of the upper index (1)niin Eq.(25),we obtain the corresponding equations for the infinite sub-region[RM,∞].

In the same manner,we obtain the following equations from the equations in (20).

Now,we attempt to solve the equations in (26)and for this purpose we reduce these equations to the following form.

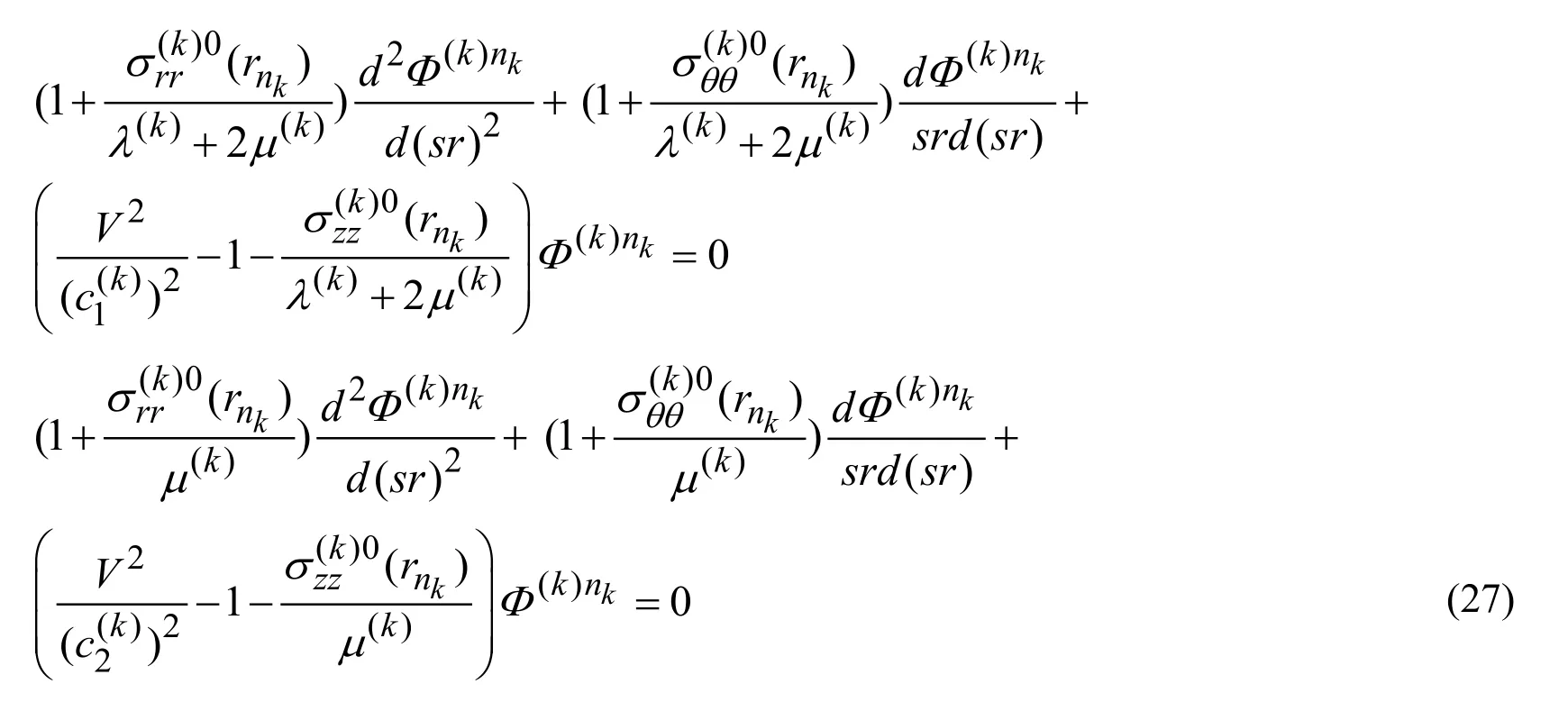
We introduce the following notation to simplify the expression of the equations in (27).

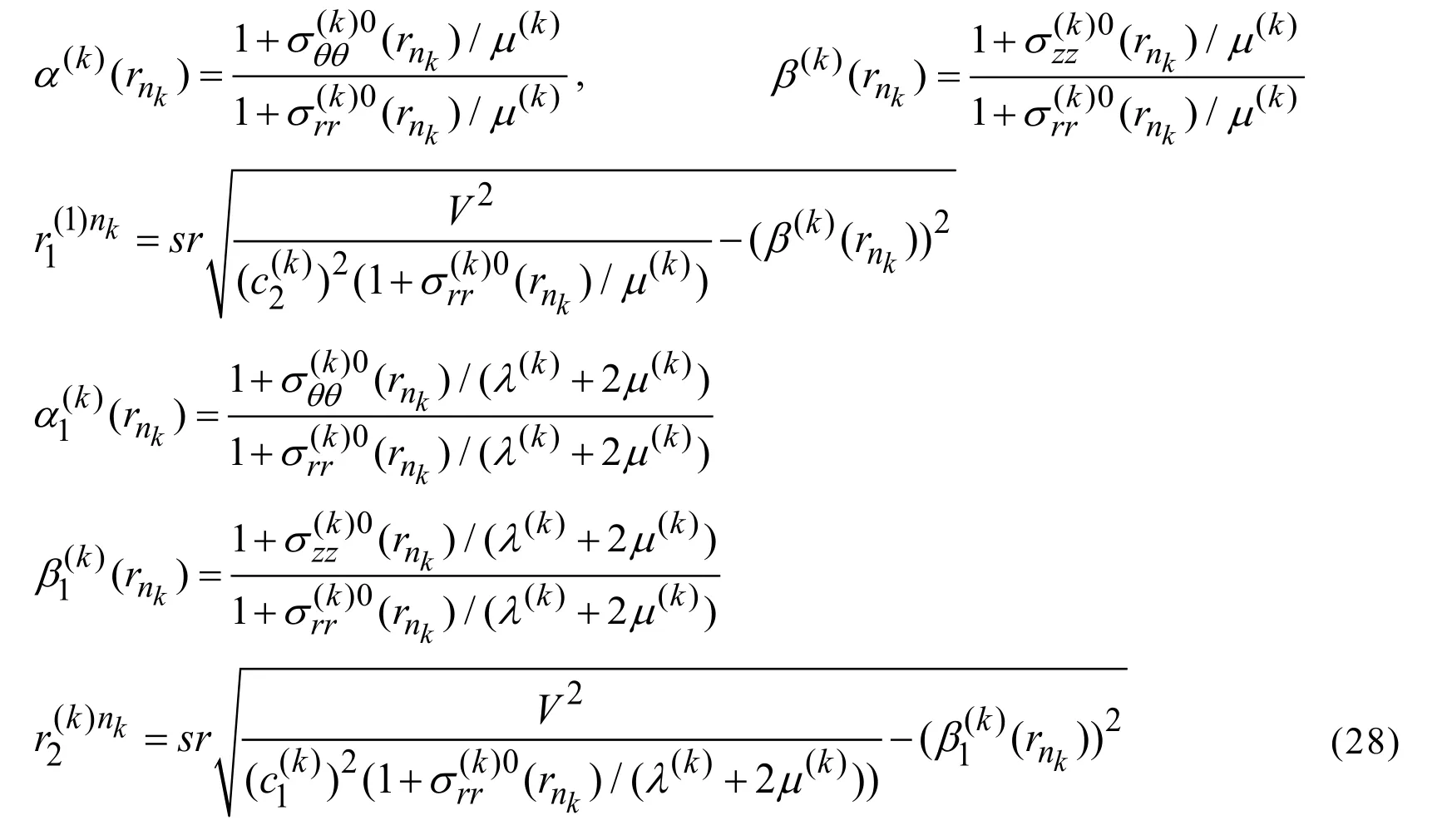
3.4 Solution to the equations in (27)

Taking the notation in (28)into consideration,the equations in (27)can be rewritten as follows.

Consequently,the equations in (29)have the following form.

According to Watson [Watson (1966)],using the substitution

The following Bessel equation for the functiony1(x)is obtained from the Eq.(30)

In a similar manner,we can write the following presentation for the potentialsand

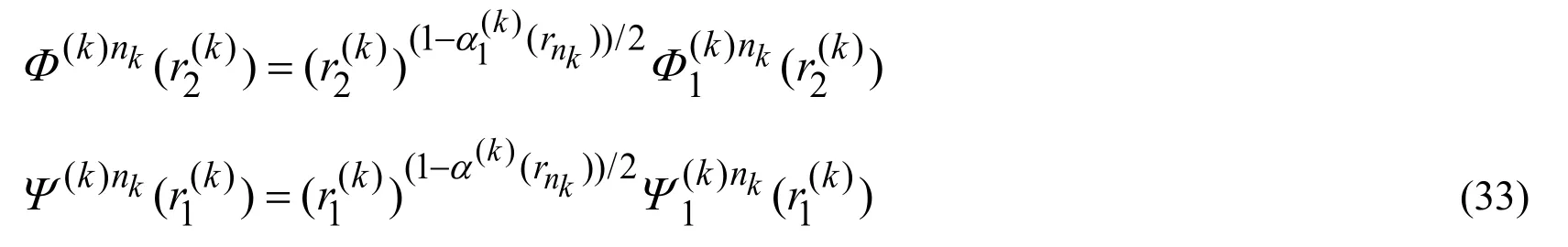
and substituting the expressions in (33)into the equations in (29),we obtain the equations

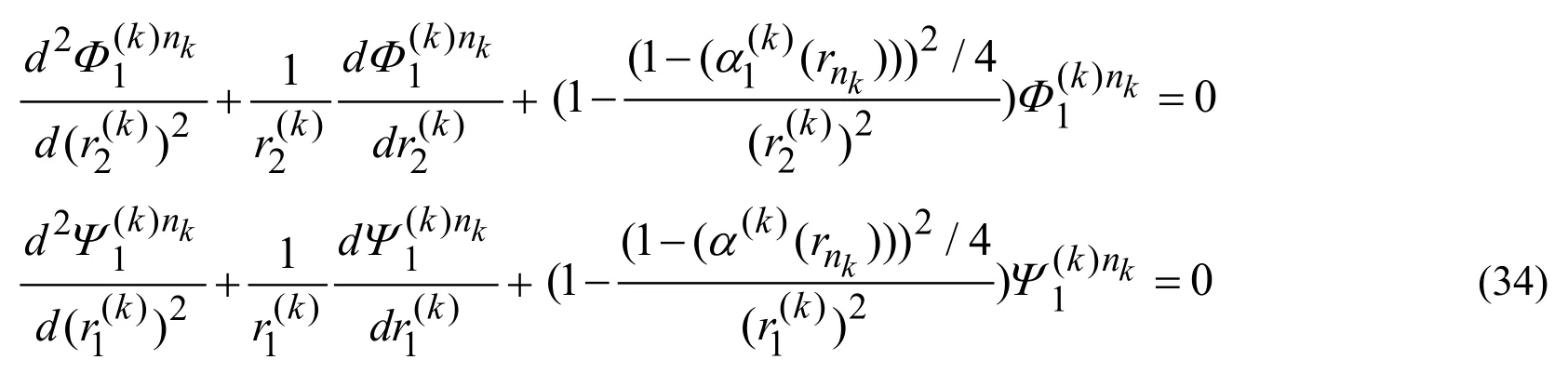
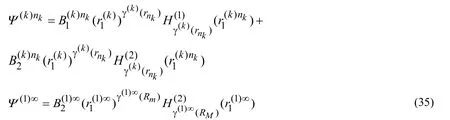
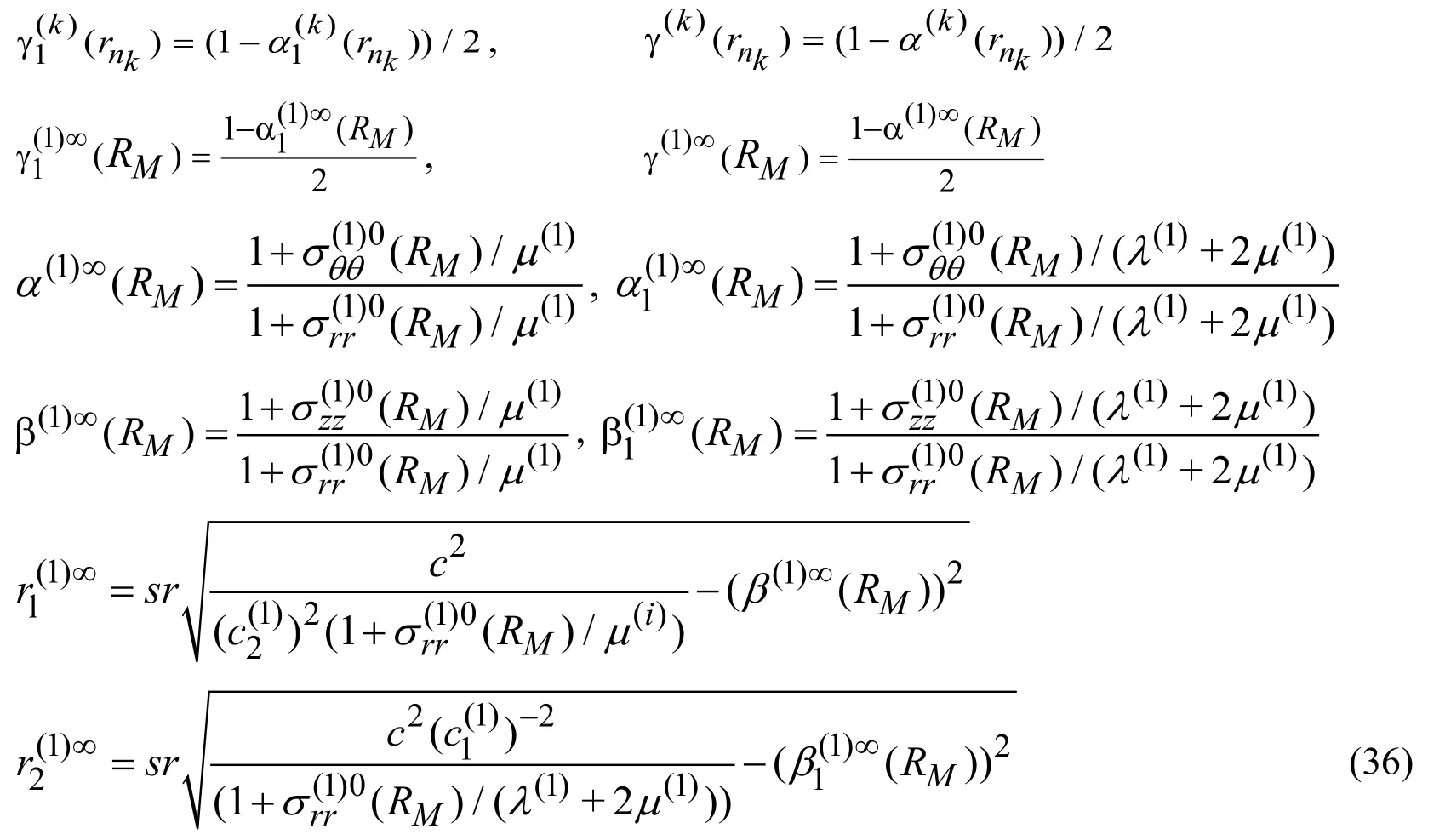
Thus,substituting the expressions in (35)into the expressions in (34)and substituting the latter ones into the expressions in (19)we determine the expressions for the Fourier transforms of the displacements which have the following form.

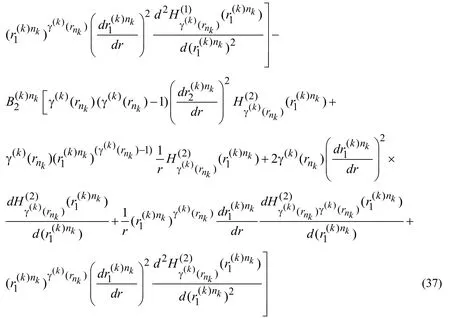
Finally,substituting these expressions into the Eqs.(16)and (17),we obtain the expressions for the Fourier transforms of the stresses.Here,we do not give these expressions in order to reduce the volume of the paper and these expressions can be easily obtained after certain mathematical calculations and transforms.Thus,substituting these expressions into the relations in (24)we obtain the system of algebraic equations for determination of the unknown constants which can be expressed as components of thedimensional vectorxwhere

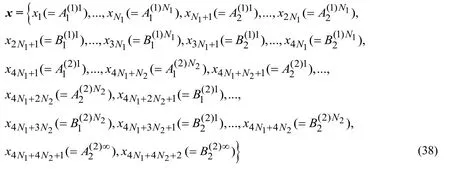
and we can present this system of equations as follows

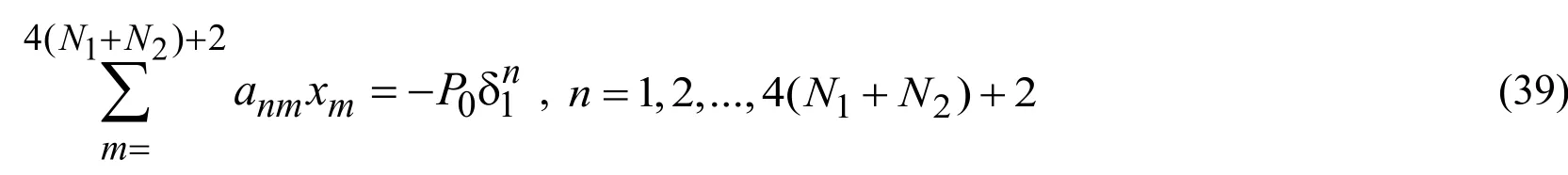
The expressions of the coefficientsanmin (39)can be easily determined from the expressions of the Fourier transforms of the stresses and displacements,the latter of which are given in (37).

In this way,we determine completely the Fourier transforms of the sought values after which their originals are found through the integrals in (13).The algorithm for calculation of these integrals has been developed and applied in the works by Akbarov et al.[Akbarov(2015);Akbarov and Mehdiyev (2018a);Akbarov and Mehdiyev (2018b);Akbarov and Ismailov (2017)] and many others listed therein.According to this algorithm,under the integration procedure,the Sommerfeld contour method is used and the improper integrals are replaced with the corresponding definite integrals,i.e.,the integration interval[0,+∞]is replaced with the finite intervaland this finite interval is divided into a certain number (denote it by)of short subintervals in each of which Gauss’s integration algorithm is employed.Under the calculation procedure,it is assumed thatandwhich are determined from the convergence requirements of the numerical results.

These and other questions related to the algorithm used here are also discussed in detail in the foregoing papers and in the monograph by Akbarov [Akbarov (2015)] and therefore here we do not consider questions related to their validity.

Finally,note that the discrete-analytical solution method which is employed in the present paper was also used in the papers by Akbarov et al.[Akbarov (2006);Akbarov,Guliyev and Yahnioglu (2017);Akbarov,Mehdiyev and Ozisik (2018);Akbarov and Panachli (2015);Akbarov and Panachli (2017)] and is also detailed in the monograph by Akbarov [Akbarov (2015)].Moreover,note that this method was also used in the work by Bagirov et al.[Bagirov,Akbarov and Seyfullayev (2018)] in which the attempt is made for consideration of the corresponding moving load problem acting in the cylindrical cavity containing the infinite elastic medium with inhomogeneous initial stresses.

Note that the discrete analytical solution method applied in the present paper is similar to that employed in the paper by Akbarov et al.[Akbarov and Bagirov (2019)].However,this method differs from the methods employed in the paper by Wu et al.[Wu,Su,Liu et al.(2018)] and others listed therein,in which the axisymmetric longitudinal wave propagation in the pressurized functionally graded elastomeric hollow cylinder is investigated.Under this investigation,the initial stresses in the cylinder are determined through the solution obtained in the papers by Batra et al.[Batra and Bahrami (2009)] and Chen et al.[Chen,Liu,Kitipornchai et al.(2017)],and the solution of the wave propagation equations is solved by employing the state-space formalism for these equations with the approximate laminate or multi-layer technique.Note that when employing the multi-layer technique,not only the values of the initial stresses in each sub layer,but also the values of the other variable coefficients are taken as constants.However,in the present method,only the values of the initial stresses are taken as the corresponding constants within each sublayer.This completes the consideration of the solution method.

4 Numerical results and discussions

Now we consider the numerical results which are obtained with employing the method described in the previous section and first we analyze the influence of the inhomogeneous initial stresses on the values of the critical velocity of the moving ring load and then we consider the results which relate to the influence of the inhomogeneous initial stresses on the response of the interface stresses to the additional moving ring load.Note that under this consideration the magnitude of the initial stresses will be estimated through the ratioMoreover,note that all the results which will be discussed below are obtained in the case whereandthe validity of which will be illustrated through the convergence of the numerical results.

Under numerical investigation,we consider the following three cases

4.1 Critical velocities of the moving ring load

Under the critical velocity,we will understand the values of the moving load velocity under which the absolute values of the stresses,displacements and strains increase indefinitely and approach infinity.For illustration of the application of this criterion,we consider the results related to the response of the interface normal stress

to the dimensionless velocity of the moving loadThe graphs of this response in Case 1 underare given in Fig.2 which are constructed for various values of the ratioIt follows from these graphs that in the cases wherethe absolute values of the interface stressincrease indefinitely and,according to this statement,the values of the critical velocity (i.e.,the values ofare determined.

Figure2:Illustration of the determination of the critical velocity

Now we consider the results which show the influence of the problem parameters and especially the influence of the initial inhomogeneous stresses (i.e.,the values of the ratioon the values ofThese values are given in Tab.1,Tab.2 and Tab.3 for Case 1 (40),Case 2 (41)and Case 3 (42),respectively.

Note that the results for the critical velocity in Case 1 underh/R=0.5andand in Case 3 under(the plane strain state)andare also obtained in the papers by Abdulkadirov et al.[Abdulkadirov (1981)] and Babich et al.[Babich,Glukhov and Guz (1986)],respectively.Moreover,all the results which are obtained in the case whereby the use of the equations in (39)and given in these tables,are also obtained in the paper by Ozisik et al.[Ozisik,Mehdiyev and Akbarov (2018)]within the scope of classical linear elastodynamics and these results coincide completely with those presented here.

Consequently,the coinciding of the present results in particular cases with the known results of other authors gives a certain guarantee of the validity of the calculation algorithm and PC programs employed in the present investigation.

Table1:Values of the dimensionless critical velocity obtained in Case 1 for various values of and

Table1:Values of the dimensionless critical velocity obtained in Case 1 for various values of and

(1)/ qµ 0.00** -0.0001 -0.0003 -0.0005 -0.0007 -0.001 0.10 0.5291 0.6593 0.7488 0.7942 0.8238 0.8536/ h R 0.15 0.5738 0.6388 0.7040 0.7427 0.7700 0.7998 0.20 0.6176 0.6498 0.6921 0.7211 0.7431 0.7686 0.35 0.7337 0.7382 0.7467 0.7543 0.7613 0.7707 0.50 0.8261* 0.8269 0.8285 0.8300 0.8315 0.8337* This result was also obtained in the paper by Abdulkadirov [Abdulkadirov(1981)].** The results obtained in the present paper under by the use of the Eq.(39)coincide with the corresponding ones obtained in the paper by Ozisik et al.[Ozisik,Mehdiyev and Akbarov (2018)] which are obtained by the use of classical linear elastodynamics.(1)/ 0 q = µ

Table2:Values of the dimensionless critical velocity obtained in Case 2 for various values of and

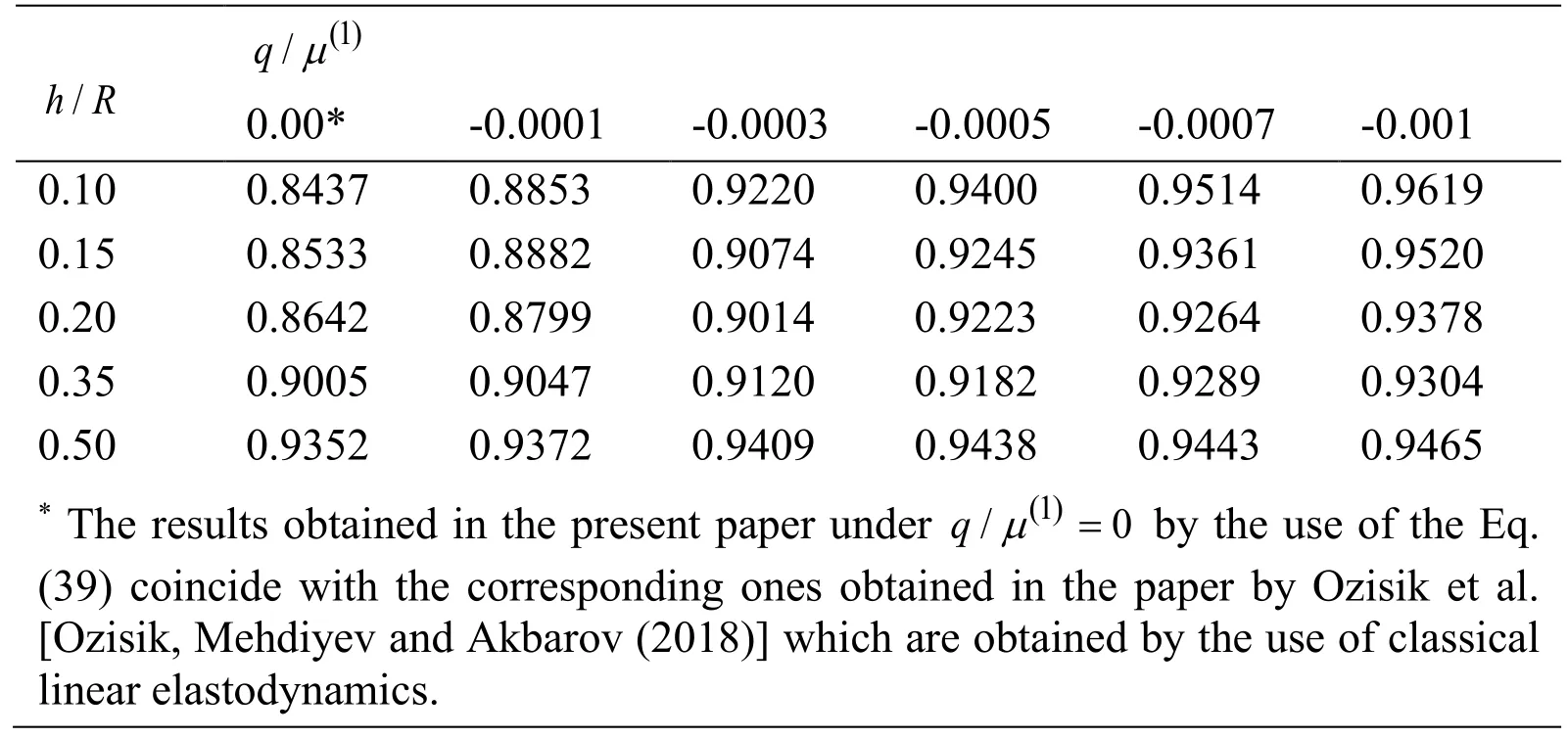
Table2:Values of the dimensionless critical velocity obtained in Case 2 for various values of and

(1)/ qµ 0.00* -0.0001 -0.0003 -0.0005 -0.0007 -0.001 0.10 0.8437 0.8853 0.9220 0.9400 0.9514 0.9619/ h R 0.15 0.8533 0.8882 0.9074 0.9245 0.9361 0.9520 0.20 0.8642 0.8799 0.9014 0.9223 0.9264 0.9378 0.35 0.9005 0.9047 0.9120 0.9182 0.9289 0.9304 0.50 0.9352 0.9372 0.9409 0.9438 0.9443 0.9465* The results obtained in the present paper under by the use of the Eq.(39)coincide with the corresponding ones obtained in the paper by Ozisik et al.[Ozisik,Mehdiyev and Akbarov (2018)] which are obtained by the use of classical linear elastodynamics.(1)/ 0 q = µ

(1)/ qµ 0.00** -0.0001 -0.0003 -0.0005 -0.0007 -0.001 0.10 0.8747* 0.8994 0.9333 0.9496 0.9594 0.9686/ h R 0.15 0.8640 0.8923 0.9217 0.9379 0.9484 0.9589 0.20 0.8742 0.8931 0.9165 0.9311 0.9411 0.9520 0.35 0.9066 0.9134 0.9232 0.9308 0.9372 0.9447 0.50 0.9396 0.9414 0.9470 0.9477 0.9524 0.9540* The results regarding the case where =0.0 is obtained in the paper by Babich et al.[Babich,Glukhov and Guz (1986)] and this result is 0.8320.** The results obtained in the present paper under/ h R by the use of the Eq.(39)coincide with the corresponding ones obtained in the paper by Ozisik et al.[Ozisik,Mehdiyev and Akbarov (2018)] which are obtained by the use of classical linear elastodynamics.(1)/ 0 q = µ

Thus,we analyze the presented numerical results related to the influence of the problem parametersq/µ(1)andh/Ron the values of the critical parameters.It follows from this analysis that the initial inhomogeneous initial stresses appearing as a result of the action of the compressional forcescause to increase the values of the critical velocity.Moreover,it follows that the increase is monotonic,i.e.,the values ofincrease monotonically with the absolute values ofq/µ(1).

Comparison of the results obtained for various values of the ratioh/Rallows us to make the following three main conclusions：

i)The magnitude of the influence of the initial inhomogeneous stresses under consideration on the values of the critical velocity of the moving load increases with decreasing of the ratioh/R;

ii)In the case where the initial stresses are absent (i.e.,in the case whereq/µ(1)=0)in the system under consideration,the values of the critical velocity increase with the ratioh/R;

iii)In the cases where the initial stresses are present in the system,however,the dependence between the critical velocity and the ratioh/Rhas non-monotonic character,i.e.,for each selected value of,there exists such a value of the ratioh/Runder which the critical velocity has its minimum value.

Note that the foregoing conclusionii)is also obtained in the papers by Akbarov et al.[Akbarov and Mehdiyev (2018a)] and Ozisik et al.[Ozisik,Mehdiyev and Akbarov(2018)],however,the conclusionsi)andiii)are characteristic and new ones for the considered problem and are obtained for the first time in the present paper.Moreover,comparison of the results obtained in the cases determined in (40),(41)and (42)and given in Tab.1,Tab.2 and Tab.3 with each other,shows that the influence of the inhomogeneous initial stresses under consideration on the values of the critical velocity of the moving load becomes more considerable in the relatively small values of the ratio

This completes the consideration and analyses of the numerical results related to the critical velocity of the moving load.

4.2 Interface stress response to the moving ring load

Here we consider only the results obtained in Case 1 and these results relate to the normal interface stress determined by the relation (43)and interface shear stress determined by the following relation.

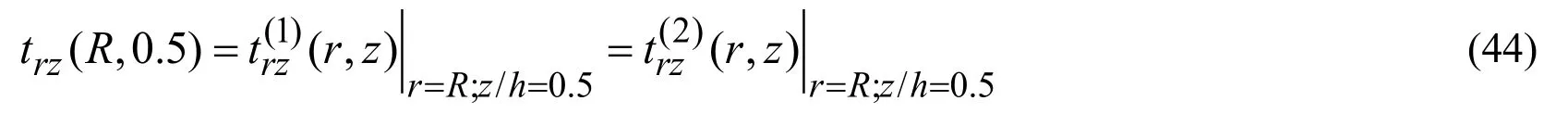
Figure3:The influence of the inhomogeneous initial stresses on the response of the interface normal stress to the load moving velocity in the cases where R / h =2

Figure4:The influence of the inhomogeneous initial stresses on the response of the interface normal stress to the load moving velocity in the cases where R / h =5

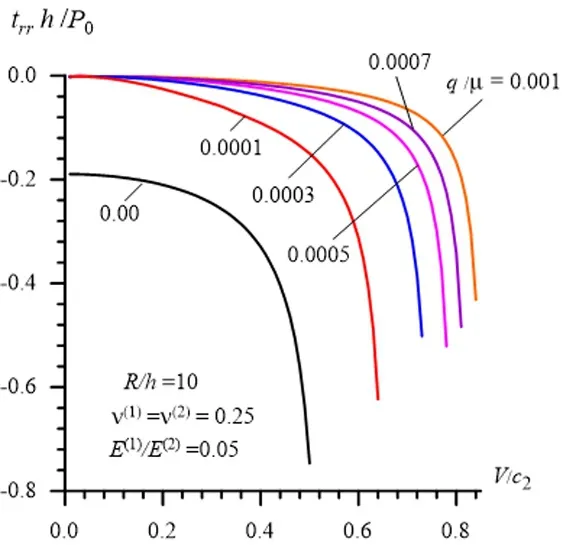
Figure5:The influence of the inhomogeneous initial stresses on the response of the interface normal stress to the load moving velocity in the cases where R / h =10

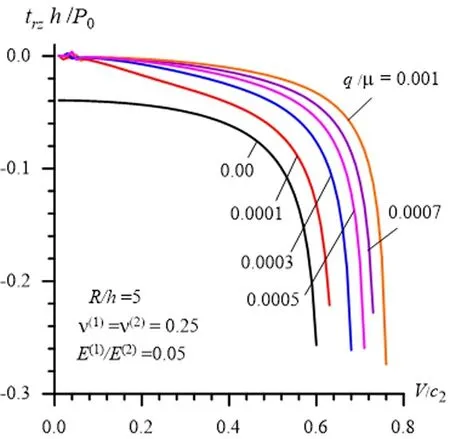
Figure6:The influence of the inhomogeneous initial stresses on the response of the interface shear stress to the load moving velocity in the cases where R / h =5

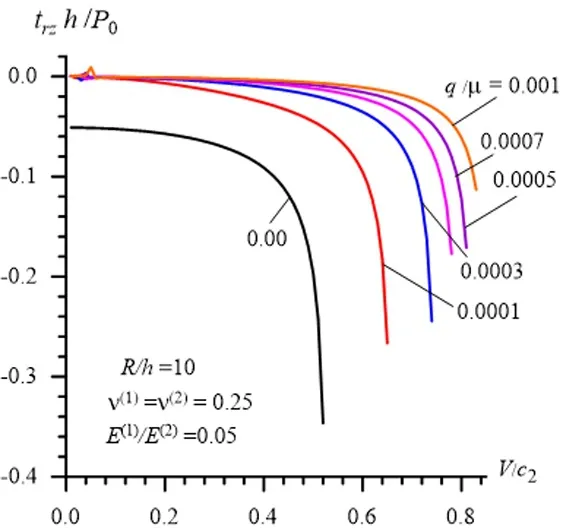
Figure7:The influence of the inhomogeneous initial stresses on the response of the interface shear stress to the load moving velocity in the cases where R / h =10

The graphs illustrating the response of the normal interface stress (43)to the moving load velocity are given in Fig.3,Fig.4 and Fig.5 which are constructed in the cases whereR/h=2Fig.3,R/h=5Fig.4 andR/h=10Fig.5.The same graphs for the interface shear stress (44)are given in Fig.6 and Fig.7 which are constructed in the cases whereR/h=5Fig.6 andR/h=10Fig.7.Note that for simplicity and clarity of illustration,in Fig.3-Fig.7 as well as in other figures which will be considered below,only the absolute values of the ratioq/µ(1)are shown.

It follows from these graphs that the considered type of inhomogeneous initial stresses cause to decrease the absolute values of the interface stresses and this decreasing agrees with well-known physico-mechanical considerations.Moreover,it follows from these results that in the cases wherethe influence of the inhomogeneous initial stresses on the interface stresses becomes more complicated,and the absolute values of these stresses decrease with the absolute values of

The graphs in Fig.3-Fig.7 also show that in selected cases the magnitude of the influence of the inhomogeneous initial stresses on the values of the stresses increases with decreasing of the ratioh/R,and this magnitude becomes more considerable in the cases where the moving load velocity approaches the corresponding critical velocities.

Comparison of the results illustrated in Fig.3,Fig.4 and Fig.5 with the corresponding ones illustrated in Fig.6 and Fig.7 shows that in the case under consideration the absolute values of the interface normal stress are greater than the corresponding ones obtained for the interface shear stress.

Figure8:Distribution of the interface normal stress with respect to the axial coordinate z / h under various values of the ratio q / µ(1)in the cases where R / h =5

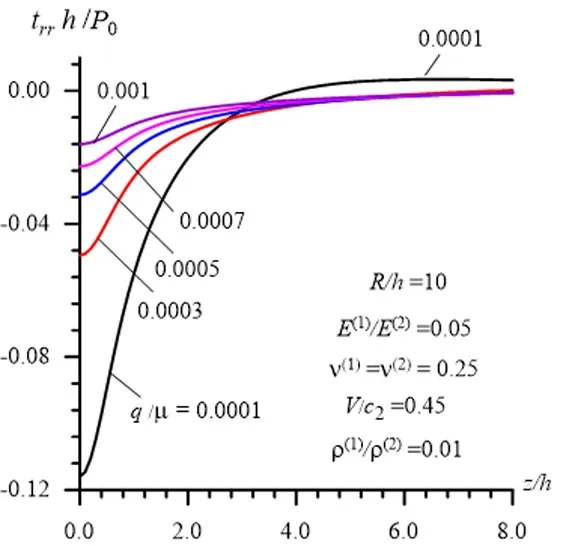
Figure9:Distribution of the interface normal stress with respect to the axial coordinate z / h under various values of the ratio q / µ(1)in the cases where R / h =10

Figure10:Distribution of the interface shear stress with respect to the axial coordinate z / h under various values of the ratio q / µ(1)in the cases where R / h =5

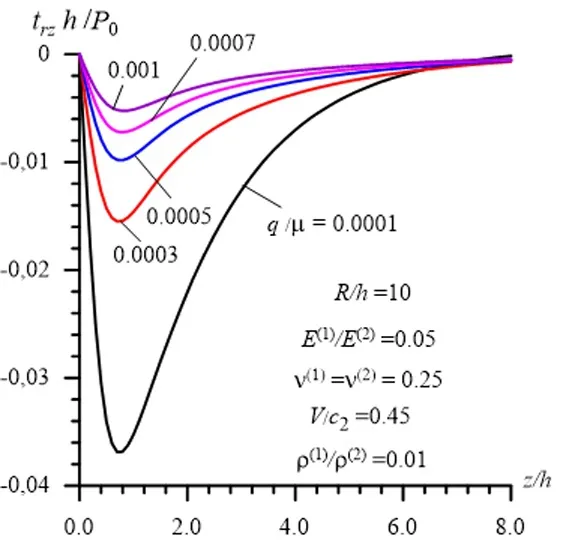
Figure11:Distribution of the interface shear stress with respect to the axial coordinate z / h under various values of the ratio q / µ(1)in the cases where R / h =10

We recall that the foregoing numerical results are obtained in the case wherez/h=0(for the interface normal stress)and in the case wherez/h=0.5(for the interface shear stress)and therefore these results cannot give any information on the distribution of the interface stresses with respect toz/hor on the influence of the inhomogeneous initial stresses on these distributions.In connection with this,we consider the graphs given in Fig.8-Fig.11 which show the distribution for the interface normal (Fig.8 and Fig.9)and interface shear (Fig.10 and Fig.11)stresses.Note that in these figures the graphs are obtained for the case whereR/h=5(Fig.8 and Fig.10)and for the case whereR/h=10(Fig.9 and Fig.11).Moreover,note that these graphs are constructed for various values of the ratiounder

Thus,it follows from these graphs that the inhomogeneous initial stresses under consideration cause to decrease the absolute values of the stresses in each interface point.This influence becomes more considerable with decreasing of the ratioh/R.

We note that the dimensionless coordinatez/his the coordinate in the moving coordinate system determined through the relation (12).In the other words,in reality,the coordinate used in Fig.8-Fig.11 isz'/hand therefore the graphs in these figures show not only the distribution of the stresses with respect to the distance from the load acting point under fixed time,but also the change of these stresses with respect to time under a fixed point on the interface between the hollow cylinder and surrounding elastic medium.

4.3 Results illustrating convergence of the numerical results

We recall that the foregoing results are obtained in the case whereandand to illustrate the validity of such selection of the numbersandas well as the ratiowe consider the numerical results which illustrate their convergence with respect to these numbers and to this ratio.For this purpose we consider the results given in Fig.12,Fig.13 and Fig.14 which are constructed in Case 1 under the worst case in the convergence sense,i.e.,underandR/h=10.These results show the convergence of the numerical results with respect to the numberunderand(Fig.12),with respect to the ratiounderandand with respect to the numberunderandNote the results obtained in the cases whereandcoincide almost completely with those obtained in the case whereand

Figure12:Convergence of the numerical results with respect to the number N2of the cylinder’s sub-regions under and

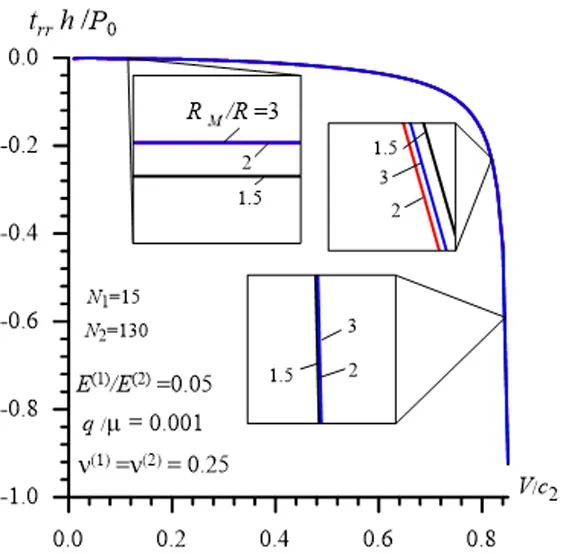
Figure13:Convergence of the numerical results with respect to the ratio under and

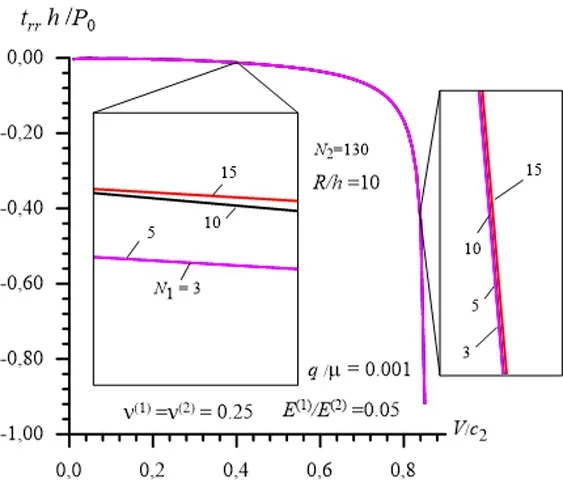
Figure14:Convergence of the numerical results with respect to the number N1under N2 =130and

Thus,the results given in Fig.12,Fig.13 and Fig.14 guarantee the validity of the selected values for the numbersN1andN2as well as for the ratioRM/Rin the convergence sense of the numerical results.

This completes the consideration of the numerical results.

Finally,note that the great difference between the numbersN1andN2,in other words,obtaining the great value for the numberN2for providing the convergence of the numerical results is explained with the significant change rate of the initial stresswith respect to the radial coordinate r within the hollow cylinder,i.e.,in the intervalR-h＜r＜R.This character of the distribution of the stressis established by direct verification of the numerical results related to the initial stresses.Consequently,it can be concluded that use of the approximate shell theories which do not exactly take into consideration the distribution of the radial initial stresses for describing the motion of the hollow cylinder,may be very approximate and unacceptable under investigation of the considered problem.

5 Conclusions

Thus,in the present paper,the axisymmetric problem related to the dynamics of the moving ring load acting in the interior of the inhomogeneous initially stressed hollow cylinder surrounded with the inhomogeneous initially stressed infinite elastic medium is studied with employing of the 3D linearized exact equations of the theory of elastic waves in initially stressed elastic bodies.It is assumed that the inhomogeneous initial stresses in the system “hollow cylinder + surrounding infinite elastic medium” are caused by uniformly distributed normal compressional forces acting at infinity in the inward radial direction.Moreover,it is assumed that after appearance of these initial stresses,the interior of the cylinder is loaded by the additional moving ring load and it is required to determine how the inhomogeneous initial stresses affect the values of the critical velocity of this moving load and on the stress state which appears as a result of the action of this additional moving load.For the solution to the corresponding problem,the discreteanalytical solution method by using the moving coordinate system and the Fourier transform is employed.Numerical results on the influence of the initial compressional forces on the values of the critical velocity and on the distribution of the interface stresses appearing as a result of the additional moving load are presented and discussed.According to these numerical results the following concrete conclusions can be made：

- The inhomogeneous initial stresses cause to increase the values of the critical velocity,and this increase is monotonic with the absolute values of the initial compressional forces acting at infinity in the inward radial direction;

- The magnitude of the influence of the initial inhomogeneous stresses under consideration on the values of the critical velocity of the moving load increases with decreasing of the ratioh/R;

- In the case where the initial stresses are absent (i.e.,in the case whereq/=0)in the system under consideration,the values of the critical velocity increase with the ratioh/R.However,in the cases where the initial stresses are present in the system,the dependence between the critical velocity and the ratioh/Rhas non-monotonic character,i.e.,for each selected value ofq/,there exists such a value of the ratioh/Runder which the critical velocity has its minimum value;

- The magnitude of the influence of the inhomogeneous initial stresses on the values of the critical velocity increase with decreasing of the ratio/,where()is the modulus of elasticity of the cylinder’s (the surrounding elastic medium)material;

- The existence of the considered type of inhomogeneous initial stresses causes to decrease the absolute values of the interface stresses which appear as a result of the action of the additional moving ring load;

- The existence of the considered type of inhomogeneous initial stresses also causes too rapid decaying of the interface stresses with the distance from the point at which the moving load acts,and with time,at the fixed interface point.

Besides all these,we can note that the method used in the present paper can also be used for investigations of more complicated problems related to the dynamics of the “hollow cylinder + surrounding elastic medium” with inhomogeneous initial stresses.