Polygamy inequalities for multiqubit W-calss states in terms of the squared Tsallis-q entanglement

YUAN Guang-Ming, DONG Ming-Hui, WANG Xue-Wen, YIN Tian-Tian, CHEN Li

(1. Qilu Institute of Technology, Jinan 250200, China;2. Anqing normal University, School of Physics and Electronic Engineering , Anqing 246113, China)

Abstract: Polygamy is an important properties for quantum entanglement. The Tsaliis-q entanglement, which is the generalization of entanglement of formation(EOF), obeys a general polygamy inequality in an arbitrary N-qubit mixed state. In this paper，we enlarge the range of q for the analytic formula of Tsallis-q entanglement and investigate the polygamy inequalities for multiqubit generalized W-class states for the squared Tsallis-q entanglement.

Key words: Polygamy; W-class state; Tsallis-q entanglement

1 Introduction

Monogamy of entanglement(MOE)[1-4]is an important property discovered recently in terms of multi-qubit entanglement. which means that quantum entanglement cannot be shared freely in multi-qubit systems. The monogamy inequality was first proposed by Coffman, Kundu and Wootters(CKW) for squared concurrence(SC)in a three-qubit systems[5]. Furthermore, Obsborne and Verstrate generalized this inequality relation to N-qubit systems[6],

C2(ρA1|A2…An)≥C2(ρA1A2)+

C2(ρA1A3)+…+C2(ρA1An)

Moreover, the monogamy inequalities were also establish for Gaussian systems[7], squashed entanglement[8], entanglement negativity[9], Entanglement of Formation(EoF)[10]and Tsallis-qentanglement(TqE)[11]. The applications of monogamy inequality include many fields of physics[12-22].As dual concept to bipartite entanglement monogamy property, polygamy property in multi-qubit systems has arised many interests by researchers for concurrence of assistance[23],

C2(ρA1|A2…An)≤[Ca(ρA1A2)]2+

[Ca(ρA1A3)]2+…+[Ca(ρA1An)]2

polygamy property has also been considered in many entanglement measures, such as entanglement of Formation, Tsallis-qentanglement[24].

2 Analytic formula of Tsallis-q entanglement

We first recall the definition of Tsallis-qentanglement[11]. For a bipartite pure state |ψ〉AB, the Tsallis-qentanglement is given by

(1)

for anyq>0 andq≠1,whereρA=trB(|ψ〉AB〈ψ|) is the reduced density matrix by tracing over the subsystem B.

For a mixed stateρAB, the Tsallis-qentanglement is defined via convex-roof extension

(2)

where the minimum is taken by all possible pure state decompositions of

Kim have established the analytic formula between Tsallis-qentanglement and Concurrence for 1≤q≤4.

Tq(|ψ〉AB)=gq(C(|ψ〉AB))

(3)

where the functiongq(x) is defined as

(4)

In the following we shall the property of analytic formula. The analytic formula holds is monotonically increasing and convex for anyq. Next we shall generalize the range ofqwhen the functiongq(x) is monotonically increasing and convex with respect to x. The monotonically increasing property ofgq(x) follow from the non-negativity of its first derivative. After a direct calculation, we find that the first derivative ofgq(x) with respect to x is always nonnegative forq≥0. The convexity ofgq(x) follow from the non-negativity of its second derivative. We can further consider the second-order derivative ofgq(x) beyond the region 1≤q≤4.

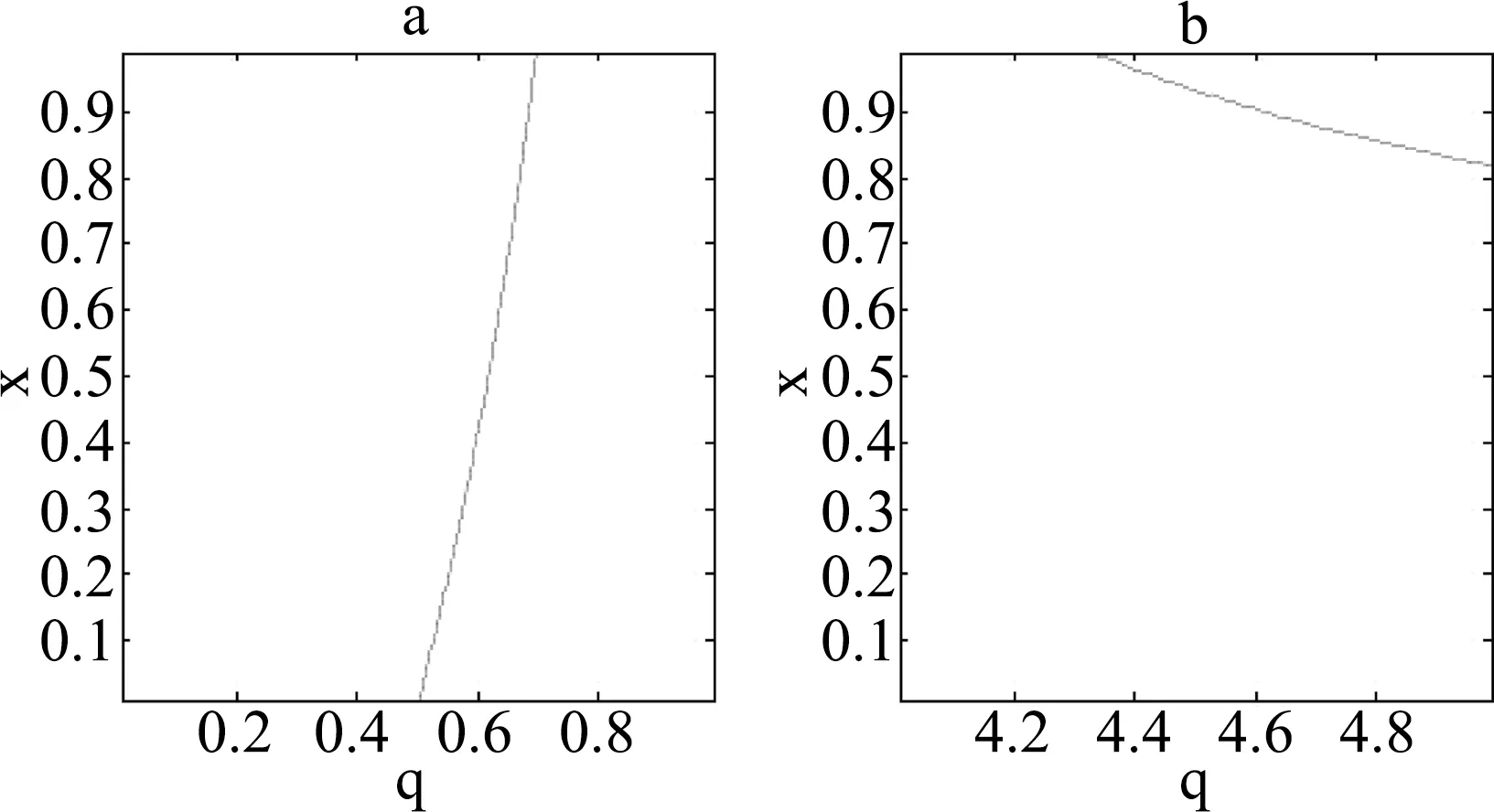
Fig.1 The plot of the dependence of x with q which satifies the equation ∂2Tq(C)/∂x2=0 for (a) q∈(0,1) and (b) q∈(4,5) respectively.

We first analyze the nonnegative region for the second-order derivativegq(x) for 0≤q≤1. Numerical calculation shows that under the condition ∂2Tq(C)/∂x2=0, the critical value of x increases monotonically with the parameterq. In
Fig. 1(a), we plot the solution (x, q) to this critical condition, where for each fixed x there exists a value ofqsuch that the second-order derivative ofTq(C) is zero. Because x varying monotonically withq, we should only consider the condition ∂2Tq(C)/∂x2=0 in the limitx→1. Whenx=1, we have

(5)

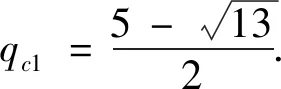
3 Polygamy inequality for multiqubit W-calss states in term of squared Tsallis-q entanglement

The n-qubit generalized W-class states |ψ〉∈HA1⊗HA2⊗…HAndefined by[25]

|ψ〉=a|000…〉+b1|01…0〉+…+bn-1|00…1〉

In the following we study the polygamy inequalities of the TqE and STqE.

3.1 For the n-qubit generalized W-class state |ψ〉∈HA1⊗HA2⊗…HAn, the TqE satisfies

proof. For the n-qubit generalized W-class state |ψ〉∈HA1⊗HA2⊗…HAn,we have

Tq(|ψ〉A1|A2…An)=gq(C(|ψ〉A1|A2…An)

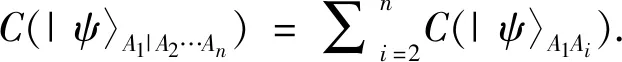
Next, we recall the lemma of W-class state[16].

Lemma.1 Let |ψ〉A1|A2…Anbe a generalized W-calss state. For any m-qubit subsystemsA1Aj1…Ajm-1ofA1…Anwith 2≤m≤n-1, the reduced density matrixρA1Aj1…Ajm-1of |ψ〉A1|A2…Anis a mixture of a m-qubit generalized W-class state and vacuum.

3.2 For the n-qubit generalized W-class state |ψ〉∈HA1⊗HA2⊗…HAn, the STqE satisfies

proof. We first consider the pure state |ψ〉 of a n-qubit generalizedW-class, we have

where in the first inequality we have used the theorem 3.2 and when 0≤a≤b,a2≤b2. The second inequality is due to the Cauchy-Schwarz inequality. The last equality is due to∑jpj=1

Next,we consider the mixture stateρA1A2…Anof a n-qubit generalizedW-class state. From Lemma.1, we have the pure decomposition ofρA1A2…An

Thus, we can obtain

where in the first inequality we have used the theorem 3.2 and when 0≤a≤b,a2≤b2. The second inequality is due to the Cauchy-Schwarz inequality. The last equality is due to ∑jpj=1. Thus we have completed the proof of the polygamy inequality for STqE in generalizedW-class state.

4 Conclusions