椭圆曲线y2=x3-x±6的整数点

（陇南师范高等专科学校 数信学院，甘肃 陇南 742500）

1 引言及预备知识

从集合论的观点看，椭圆曲线实际上就是由它上面的点的集合所构成的，并且可以由其点集唯一确定.椭圆曲线可看作点集构成一个可交换的加法群.一般地，将定义在某一数域上的椭圆曲线E：y2=x3+ax+b上点的集合记作E().设Q 为有理数的集合，一般来讲，有3 个与E(Q)有关的基本问题，分别为确定集合E(Q)中是否有无穷多个有理点，求出集合E(Q)中所有的有理点，求出集合E(Q)中某一个特定的有理点.在一般情况下，这3 个问题都很困难.根据Mordell 有限基定理，椭圆曲线有理点集E(Q)可以有限生成，但生成过程未知[1-2]，而著名的21 世纪7 个“千禧难题”之一的BirchSwinnerton-Dyer 猜想（BSD 猜想）[3]就是与椭圆曲线有理点分布有关的一个极具挑战性的难题.BSD 猜想是寻找有关E(Q)的大小信息，是要找到什么情况下椭圆曲线E(Q)有无穷多个有理解，而在具体情况下椭圆曲线E(Q)有有限个解.基于此，与BSD 猜想有关的问题——确定椭圆曲线的整点问题就显得非常重要，也是数论和算术代数几何中的重要问题[4-5].

目前，对于椭圆曲线y2=(x+a)(x2-ax+p)的整点问题，当a=-2时，已经找到对应椭圆曲线所有整点的p值：p=7，1 5，1 8，2 3，3 1，4 3，139[6-12]；当m=4p-8=q+1或m=2p-8=q+1且p≡/1(mod8)时，已经找到对应椭圆曲线全部整数点[13].当a=2时，已经找到对应椭圆曲线所有整点的p值：p=7，15，27，31，43[14-18]；当a=± 2时，已经找到了当p=36s2-5，s为正奇数，且6s2-1，12s2+1均为素数时的全部整数点[19-20].

本文对a=±2，p=3的情况进行了讨论，得到了椭圆曲线y2=x3-x± 6没有正整数点的结论.文中N+为正整数集合.

2 主要结果及证明

定理椭圆曲线

仅有整数点为(x,y)=(-2,0)及(x,y)=(2,0).

证明设椭圆曲线y2=x3-x± 6的整数点为(x,y)，由式（1）可知

显然，(x,y)=(-2,0)及(x,y)=(2,0)是式（2）的解.下面讨论式（2）的非平凡解.

设d=gcd(x±2,x2∓2x+3)，由于x2∓2x+3=(x±2)2∓6(x± 2)+11，则d11.因此d=1,11.

首先，讨论

的整点问题.

当d=1时，可令x+2=a2,x2-2x+3=b2,y=±ab,gcd(a,b)=1,a,b∈N+.因为a2≡0,1,4(mod8)，所以x≡a2-2≡-2,-1,2(mod8)，于是有x2-2x+3≡(-1)2-2×(-1)+3 ≡6(mod8)或x2-2x+3≡(±2)2-2× (±2 )+3 ≡3 (mod8)，即x2-2x+3 ≡6,3 (mod8)，而b2≡0,1,4 (mod8)，矛盾.因此，当d=1时，椭圆曲线y2=x3-x+6仅有整数点(-2,0).

当d=11时，可令x+2=11a2,x2-2x+3=11b2,y=±11ab,gcd(a,b)=1,a,b∈N+.易得(11a2-3)2-11b2=-2 .

令u=11a2-3,v=b，则有u2-11v2=-2 .由引理3～4 可知，不定方程u2-11v2=-2 的全部解只有一个结合类，且由表出.于是可以得到递归序列

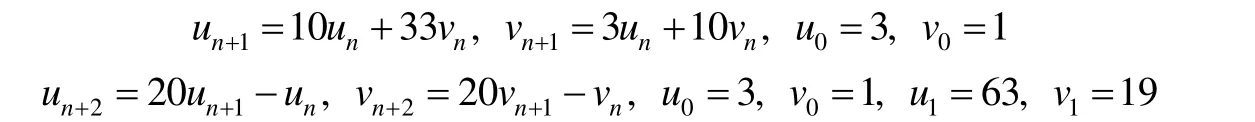
及序列性质：un≡1 (mod2)，un≡0 (mod3)，u2n≡3 (mod11)，u2n+1≡-3 (mod11)，u4n≡u4n+1≡3 (mod20)，u4n+2≡u4n+3≡-3 (mod20).

由un=11a2-3 ≡0 (mod3)可知，2a2≡0 (mod3)，a≡0(mod3).又un为奇数，则a必为偶数，于是6|a.不妨设a=6k，那么，要使un=11a2-3=396k2-3≡±3 (mod20)成立，则一定有5k，n≡2,3 (mod 4).于是有30a.因此un=11a2-3 ≡-3 (mod9 900)，也即

因此，由式（4）及序列un模4，25，11 的余数规律有

然而，同余方程组（5）～（6）均无解.所以，不存在整数n，使得un=11a2-3成立.这也说明了，当d=11时，椭圆曲线y2=x3-x+6没有整数点.

其次，讨论

的整点问题.

当d=1时，可令x-2=a2,x2+2x+3=b2,y=±ab,gcd(a,b)=1,a,b∈N+.因为a2≡0,1,4(mod8)，所以x≡a2+2≡-2,3,2(mod8)，于是有x2+2x+3≡(±2)2+2× (±1)+3 ≡3 (mod8)或x2+2x+3≡ 32+2 × 3+3 ≡2 (mod8)，即x2+2x+3 ≡2,3 (mod8).而0,1,4≡b2≡x2+2x+3 ≡2,3 (mod8)不可能成立.因此，当d=1时，椭圆曲线y2=x3-x-6仅有整数点(2,0).

当d=11时，可令x-2=11a2,x2+2x+3=11b2,y=±11ab,gcd(a,b)=1,a,b∈N+，易知(11a2+3)2-11b2=-2 .

令u=11a2+3,v=b，则u2-11v2=-2 .由un=11a2+3 ≡0 (mod3)可知，2a2≡0 (mod3)，a≡0(mod3).由于un为奇数，则a必为偶数，于是6a.不妨设a=6k，那么，要使un=11a2+3=396k2+3≡±3 (mod 20)成立，则一定有5k，且n≡0,1(mod4).此时30k，因此un=11a2+3 ≡3 (mod9 900)，也即

综上可知，椭圆曲线y2=x3-x+6仅有整数点(x,y)=(-2,0)，椭圆曲线y2=x3-x-6仅有整数点(x,y)=(2,0). 证毕.