基于密度和半监督学习的数据修复与聚类

张倩倩，李国和,3，郑艺峰,4,5

(1.中国石油大学(北京) 石油数据挖掘北京市重点实验室，北京 102249；2.中国石油大学(北京) 信息科学与工程学院，北京 102249；3.石大兆信数字身份管理与物联网技术研究院， 北京 100029；4.闽南师范大学 数据科学与智能应用福建省高等学校重点实验室， 福建 漳州 363000；5.闽南师范大学 计算机学院，福建 漳州 363000)

0 引 言

由于硬件、软件、人为等因素的影响，数据在收集、存储、传输等过程会出现数据质量问题。数据修复是数据质量中的一个重要组成部分，因此数据修复算法的研究是当务之急，对数据挖掘质量起着积极作用。数据修复算法是根据约束和规则对关系数据库进行修复，如何获得正确的约束和规则是难点，如何对简单数据集进行修复是一个需要解决的问题。现有的数据修复算法可以分为3类：基于约束的数据修复算法[1-5]、基于规则的数据修复算法[6-8]以及人工修复算法。现有修复算法不适用于简单数据集，本文在现有修复算法上加入密度信息和成对约束信息，对现有修复算法进行扩展，使其不仅提高修复正确率而且适用于简单数据集。

1 相关研究

基于密度的聚类算法可比较成功识别噪声数据并丢弃处理[9-11]。但很多数据集往往存在大量不精确数据，将其丢弃必然影响聚类效果，因此需要对此类数据进行修复，以减小对聚类效果影响。现有的数据修复算法只适合于关系数据库中的数据修复，需要知道约束函数或者规则，基于约束的修复侧重点在于从数据库中挖掘出相关约束，例如函数依赖[1]、条件函数依赖[2]、近似函数依赖的挖掘[3]，这些算法侧重于约束的挖掘，利用所得的约束对数据集进行修复[4,5]。利用规则对数据集进行修复[6-8]则需要用户对数据库有较深的理解，这种修复更准确，但是不易操作。以上的数据修复算法都不适合具有简单模式的数据集，即不含有约束或者规则的数据集。

Song等提出了一种基于密度的最优修复和聚类算法[12](DORC)，同时进行数据修复和数据聚类，实验结果表明DORC能提高聚类精度和修复正确率。不足之处在于，DORC算法修复噪声数据会选择离其最近的非噪声数据，无法有效保证修复和聚类结果的正确性。例如，分别位于边界线两侧的两栋临近建筑，如果其中一栋建筑被识别为噪声数据，则会错误的将两栋建筑修复到边界线的同一边，在聚类时会错误的将两栋建筑划分为一个村庄，从而导致聚类结果不正确。为了解决上述问题，引入实例间的成对约束，利用背景知识约束修复和聚类过程，从而进一步提高聚类精度和修复准确率。

本文提出使用基于成对约束和最小修复原则的方法进行修复和聚类，首先将CL和ML约束信息用于指导数据修复和临时簇的形成，再对形成的临时聚类簇进行约束检验；若违反，则在违反约束的簇上，运行聚类算法进行二次簇的划分，得到最后的聚类簇。算法的优点在于：①同时对数据进行数据修复和数据聚类。②充分利用数据集本身的密度信息和现有的背景知识，不需要额外的完整性约束或规则。

定义1 信息系统：信息系统表示为K=(U,A,VS)， 其中U={u1,u2,…,u|P|} 为对象集合 (|U| 为集合元素个数，对象ui∈U也称为样本，对象集U也称为样本集)；A={ai|i=1,2,…,k} 为属性集合；VS={Vai|i=1,2,…,k}，Vai为对象属性ai的值域，表示对象u∈U在ai∈A上的投影，即ai：U→Vai，ai(u)∈Vai。

定义2 决策表：信息系统K=(U,A,VS)， 若C⊆A，D⊆A， 并且C∩D=Φ，C∪D=A， 称C为条件属性集，D为决策属性集，信息系统K为决策表，记为DT=(U,C∪D,VS)。

对于∀ai∈A，ai(u)≠EMPTY(空)，K为完备信息系统，否则，∃ai∈A，ai(u)=EMPTY(空)，K为不完备信息系统。其中，EMPTY是空值，表示值存在，但不知具体值。

对于A′⊆A,K′=(U,A′,VS)， 称K′为K的信息子系统。

更直观看，K′=(U,A′,VS) 为完全信息子系统，也可理解为以∀ai∈A′为坐标， |A′| 为维数，K′也成为关于A′样本空间，∀u∈U为样本子空间点。

定义3 距离函数δ： 对于完全信息子系统K′=(U,A′,VS)， ∀ui,uj∈U， δ:U×A′→R+, 满足非负性δ(ui,uj,A′)≥0、 对称性δ(ui,uj,A′)=δ(uj,ui,A′) 和同一性当且仅当uj=ui时δ(ui,uj,A′)=0， 则称δ是关于属性集A′样本间的距离函数。

定义4ε邻居、ε邻居集、邻域密度η：对于完全信息子系统K′=(U,A′,VS)， ∀ui,uj∈U， 如果δ(ui,uj,A′)≤ε(邻域距离)， 则称ui和uj是关于属性集A′的ε邻居。集合S(ui,A′,ε)={uj|∀uj∈U, δ(ui,uj,A′)≤ε} 为样本ui关于属性集A′的ε邻居集，η=|S(ui,A′，ε)| 称为ui关于属性集A′的邻域密度。关于属性集A′的ε邻居的邻居矩阵h(ui,uj,A′,ε)

(1)

h(ui,uj,A′,ε)=1表示ui和uj是关于属性集A′的ε邻居，反之表示ui,uj不是关于属性集A′的ε邻居。

定义5 中心点，边界点，噪声点：对于完全信息子系统K′=(U,A′,VS)， ∀ui,uj∈U给定的距离阈值ε和密度阈值η，对于点ui，如果 |S(ui,A′，ε)|≥η则称ui为关于属性集A′的中心点，如果 |S(ui,A′，ε)|<η但ui是关于属性集A′的中心点uj的ε邻居，即δ(ui,uj,A′)<ε， 则ui称为关于属性集A′的边界点，否则ui称为关于属性集A′的噪声点。

对于完全信息子系统K′=(U,A′,VS)， 给出关于属性集A′的核心点集、边界点集和噪声点集定义：

核心点集

Cest(U,A′,ε,η)={ui|∀ui∈U,|S(ui,A′,ε)|≥η}

(2)

边界点集

Best(U,A′,ε,η)={ui|∀ui∈U,|S(ui,A′,ε)|<η, ∃uj∈Cest(U,A′,ε,η),δ(uj,ui,A′)<ε}

(3)

噪声点集

Nest(U,A′,ε,η)=U-Cest(U,A′,ε,η)∪Best(U,A′,ε,η)

(4)

定义6 样本修复：对于完全信息子系统K′=(U,A′,VS)， 样本修复为函数映射λ∶U→U，λ(ui) 为样本ui∈U修复之后的数据，修复代价是

Δ(K′,λ)=∑∀ui∈Uω(ui,λ(ui),A′)

(5)

其中，ω(ui,λ(ui),A′) 表示单个数据修复代价，例如当修复前后的数据不一致时，可以令修复代价为1，一致时为0，也可以用修复前后的数据距离(编辑距离，曼哈顿距离等)作为修复代价。

定义7 成对约束：成对约束信息包含Must-Link(ML)约束集和Cannot-Link(CL)约束集，对于样本集U，ui,uj是样本集的样本，如果ui,uj两个样本的label(标签)相等，则两个样本在聚类时一定要属于同一类，如果两个样本标签不同，则两个样本在聚类时一定不能属于同一个聚类簇，即：

如果 (ui,uj) ∈ML， 则ui.label=uj.label， ML(ui,uj)=1否则ML(ui,uj)=0。

如果 (ui,uj)∈CL则ui.label≠uj.label， CL(ui,uj)=1否则CL(ui,uj)=0。

定义8 基于密度的半监督修复与聚类(SDORC)：对于完全信息子系统K′=(U,A′,VS)， 距离阈值ε，密度阈值η，成对约束CL，SDORC为

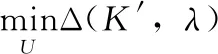
2 基于密度的半监督修复与聚类算法

DORC算法[12]有效利用了样本集内部的密度信息，改善了数据的修复准确率和聚类精度，但是在很多实际应用中，获取无标签数据的同时会得到一部分背景知识(成对约束关系或样本的标签信息，本文采用成对约束信息)。DORC没能充分利用得到的背景知识，本文在DORC算法的基础上，将得到的背景知识用于指导数据的修复和聚类过程得到基于密度和半监督学习的修复与聚类算法(SDORC)，以期得到更好的修复准确率和聚类精度。

2.1 将SDORC问题转化为整数线性规划问题

在这部分，将SDORC问题转换为整数线性规划问题：

假设变量x(ui,uj,A′,ε)∈{0,1},x(ui,uj,A′,ε)=1表示将样本ui修复到uj，相应的修复代价表示为ωij=ω(ui,uj,A′)， 否则x(ui,uj,A′,ε)=0。 对于完全信息子系统K′=(U,A′,VS)， 任何一个样本如果修复只能在不违反CL约束的情况下修复到一个位置(不能同时修复到不同的样本点，当i=j时表明该样本点没有进行修复操作)，对于任意的样本点ui

∑∀ui∈Ux(ui,uj,A′,ε)CL(ui,uj)=1

(6)

对于完全信息子系统K′=(U,A′,VS)， 修复完成之后，可能有多个样本点同时修复到同一个样本点，修复后uj的邻居样本数表示为

c(uj,A′,ε)=|{ui|∀ui∈U,δ(ui,uj,A′)≤ε}|

(7)

c(uj,A′,ε) 记录了样本点uj在ε距离范围内的邻居点的个数。

使yj=1表示样本点uj的ε邻居个数不少于η个(核心点)，否则yj=0，n表示样本集U的样本个数，满足下式

(8)

修复完成后所有的数据都是非噪声数据，即所有样本点不是核心样本点就是边界样本点(邻居点中有核心点)，即

(9)

对于上面给定的式(6)，式(8)，式(9)， SDORC问题可以转化为下面的整数线性规划问题(ILP)：

目标函数

约束条件

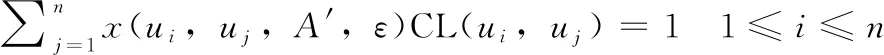
(10)

2.2 SDORC算法的相关定义

将式(10)中的变量取值范围放松至为0到1之间的实数，可以将整数线性规划问题(ILP)转化为线性规划问题(LP)。

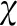
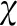
(11)

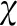
定义10 临时聚类簇：如果一个核心对象ui满足(ui，uj)属于ML，则将ui加入到ui的近邻集中，然后利用密度相连概念形成聚类簇，此时是在满足ML约束忽略部分CL约束的情况下形成的聚类簇，称之为临时聚类簇。

定义11 最终聚类簇:临时聚类簇的形成可能违反部分CL约束，在每一个临时聚类簇上检验是否有违反CL的聚类簇，如果没有违反则此临时聚类簇便是最终聚类簇，如果违反，则在违反的聚类簇上运行算法，进行临时聚类簇的再次划分或合并，形成最终聚类簇。

2.3 SDORC算法步骤

根据给定的密度阈值和距离阈值和成对约束初始化x,y， 求噪声数据，在满足ML约束的情况下进行噪声数据的修复形成临时聚类簇，在所有违反CL约束的临时聚类簇上进行临时簇的再分形成最终聚类簇，此时满足CL和ML的聚类簇就是最终聚类簇。

算法: SDORC=(U,h,ε,η,CL,ML)

输入： 样本集合U， 邻居矩阵h， 距离阈值ε， 密度阈值η， 成对约束CL，ML

输出： 聚类簇

步骤1

(1)N=N(h)

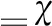
(3) while N≠Φ

(4) 找到最大yjandyj<1 anduj∈U

(5) if |N|-|(ui,uj)∈CL|≥η(1-yj) then

(6) repeat

(7) If ∃ui使 (ui,uj)∈ML andui∈N

(8)xii=0,xij=1,N=N-{ui}

(9) else

(10) 找到最小wijandui∈N(h)

(11)xii=0,xij=1,N=N-{ui}

(12) untilη(1-yj) times

(13)yj=1,N=N-({uj}∪{uk|hij=1})

(14) else

(15) forui∈Ndo

(16) finduk∈U-Nwith minimumwikand (uk,ui)∉CL

(17)xii=0,xik=1,N=N-{ui}

步骤2

(18) 基于密度可达和ML得到临时聚类簇(TC)

(19) repeat

(20) 如果TC中有违反CL的聚类簇

(21) 根据ML和CL进行合并或者分裂

(22) until |TC| 次

(23) return 聚类簇

SDORC算法的简要流程如下：

首先初始化各个参数，然后根据距离矩阵求出所有的噪声数据。当存在噪声数据时，在非核心点中找到最有可能成为核心点的数据点uj；如果现有噪声点的个数能保证uj成为核心点，在噪声点中依次找到修复代价最小的点ui，将其修复到点uj，直到uj成为核心点，如果噪声点的个数不能使uj成为核心点，则对噪声点中的每一个点找到修复代价最小的点uw，将其修复到点uw，直到所有噪声数据都被修复。

在形成的临时聚类簇上检测是否违反CL约束，如果违反CL约束，找出临时聚类簇上违反的所有CL约束形成CL1，然后找出CL1上最短距离的数据对，将数据对分开形成两个样本集data1和data2；对CL1上的所有数据对，分别计算距离data1和data2的距离，选择距离最近的样本集，将数据对中的数据分别加入距离较近的样本集中；然后对临时聚类簇的剩余数据运行KNN算法，形成最终聚类簇。

3 实验与分析

3.1 性能评价标准

聚类精度: 聚类精度我们采用纯度[13](purity)度量，以每个聚类簇中标签数量最多标签作为评价标准，即

Purity的值越大表示聚类精度越高。

修复精度：修复精度表示修复位置λ(ui) 和实际位置truth(ui) 的距离，根均方误差(RMS)来衡量

修复误差越小，修复精度越高。

修复正确率：修复精度只考虑了修复前后数据的距离，没有考虑修复是否相对正确，例如一条小河两边的两所房屋，它们地理位置非常接近，但是却属于不同的村庄，这个时候简单的将一所房子的位置修复到另一所房屋就会导致样本集修复的错误，为了平衡距离和约束的关系，提出下面的修复正确率

其中，ωi表示样本ui修复正确的权重，error越小，修复精度越高。

3.2 餐馆样本集实验结果及其分析

为了验证SDORC算法是基于约束修复算法的扩展，在餐馆数据集上进行实验，餐馆数据集是包含112个副本的864条餐馆记录的样本集，通常用于记录匹配。每组副本都可以看作一个类，每条记录包含4个属性，分别是名字、地址、城市和餐馆类型。在此实验中采用编辑距离作为距离函数，为了验证算法修复正确率，我们按照一定的脏数据比例将数据在一定范围内进行随机改变以获得不同程度的脏数据集。此数据集具有完整性约束(函数依赖关系(名字，地址)→城市)，现有的数据修复和聚类方法可以应用在此数据集上，对比实验采用基于函数依赖的数据修复算法(FD)[5]、半监督聚类(CDBSCAN)[10]以及同时修复和聚类算法(DORC)[12]，表1表示密度阈值和距离阈值一定的情况下，不同脏数据率下的聚类精度，表2表示距离阈值和密度阈值一定时，不同脏数据率下的修复精度。

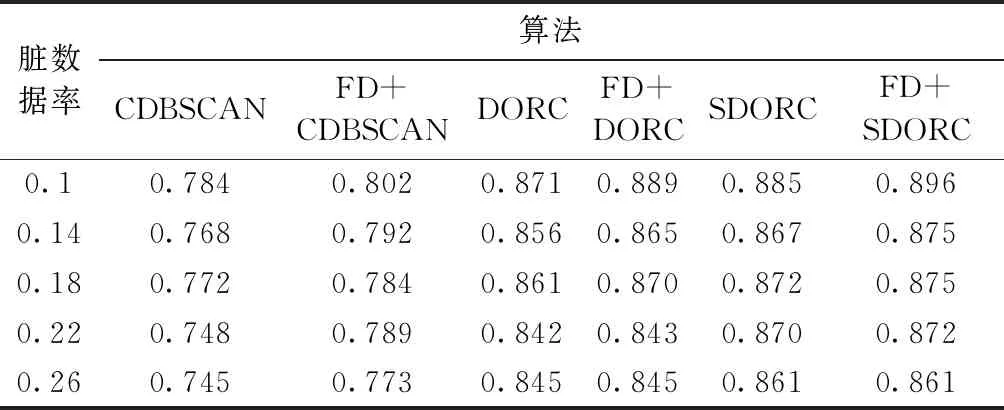
表1 不同脏数据率下各个算法的聚类精度

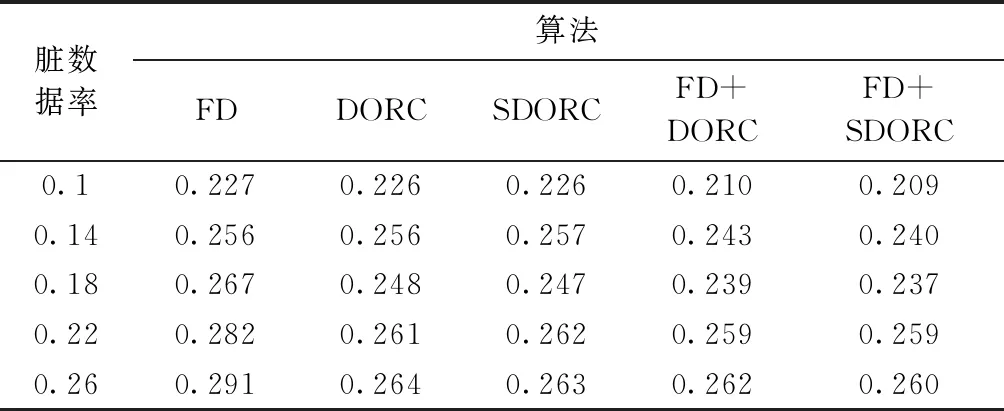
表2 不同脏数据率下各个算法的修复正确率

由表1可知，当不对数据进行修复操作时的聚类精度最低，因为此时含有不精确数据，会对聚类结果产生影响；利用FD算法先对数据进行修复然后再聚类，聚类精度会有一定程度的提高，因为此时一些脏数据会被修复成正确数据；仅仅使用DORC算法时，相比先修复再聚类的方法，聚类精度有了明显提高，在使用DORC算法之前先对数据集用FD进行修复，又会有精度的提高，使用SDORC算法相对DORC算法聚类精度有了一定提高；SDORC考虑了背景知识，使修复更为正确，如果先使用FD算法，再使用SDORC，聚类精度还有一定程度的提高，说明SDORC是现有数据修复算法的拓展。

脏数据比例一定的情况下，聚类精度随距离阈值的变化如图1所示；聚类精度随密度阈值的变化如图2所示；修复正确率随距离阈值的变化如图3所示；修复正确率随密度阈值的变化如图4所示。

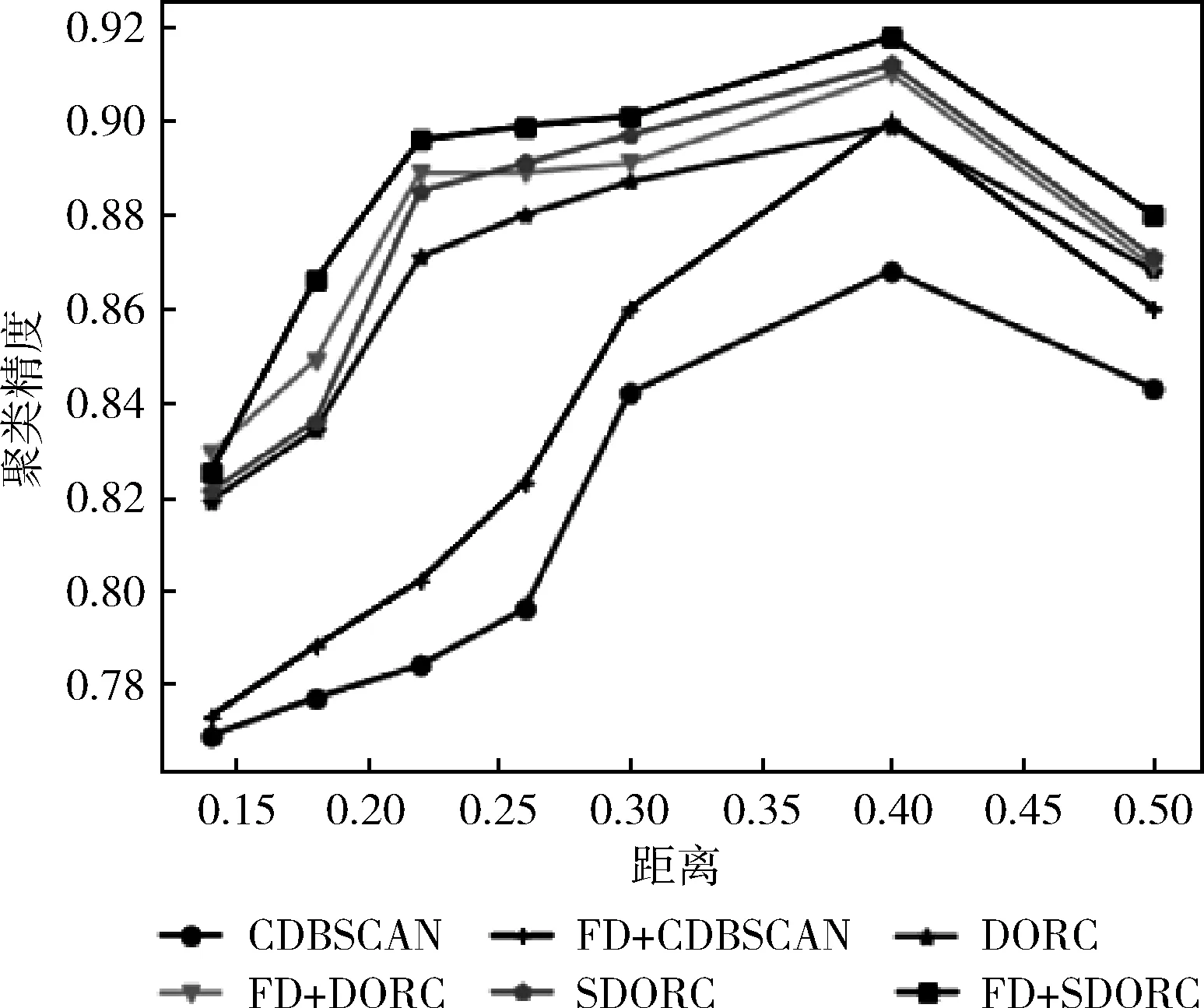
图1 聚类精度VS距离阈值

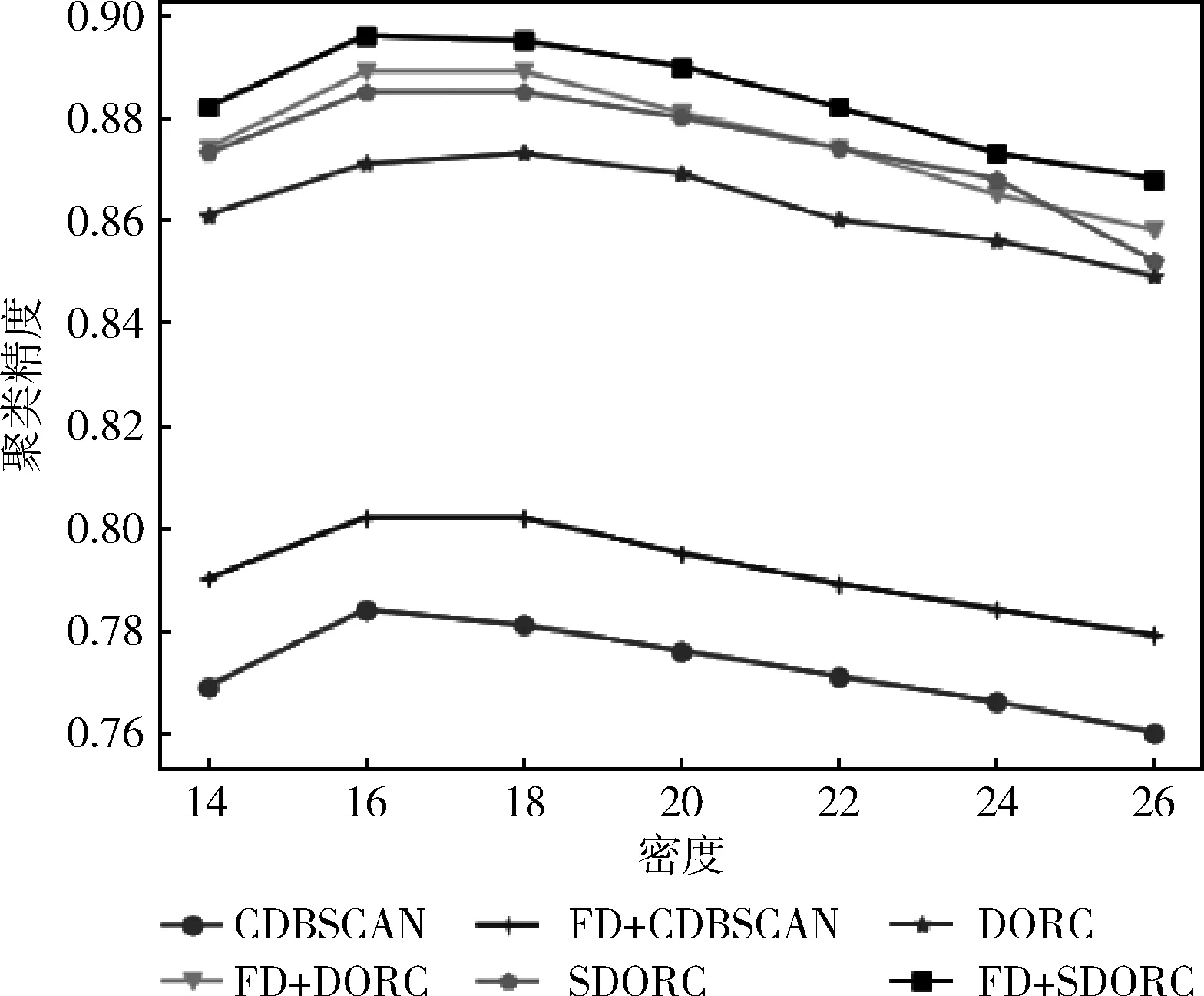
图2 聚类精度VS密度阈值

图3 修复正确率VS距离阈值

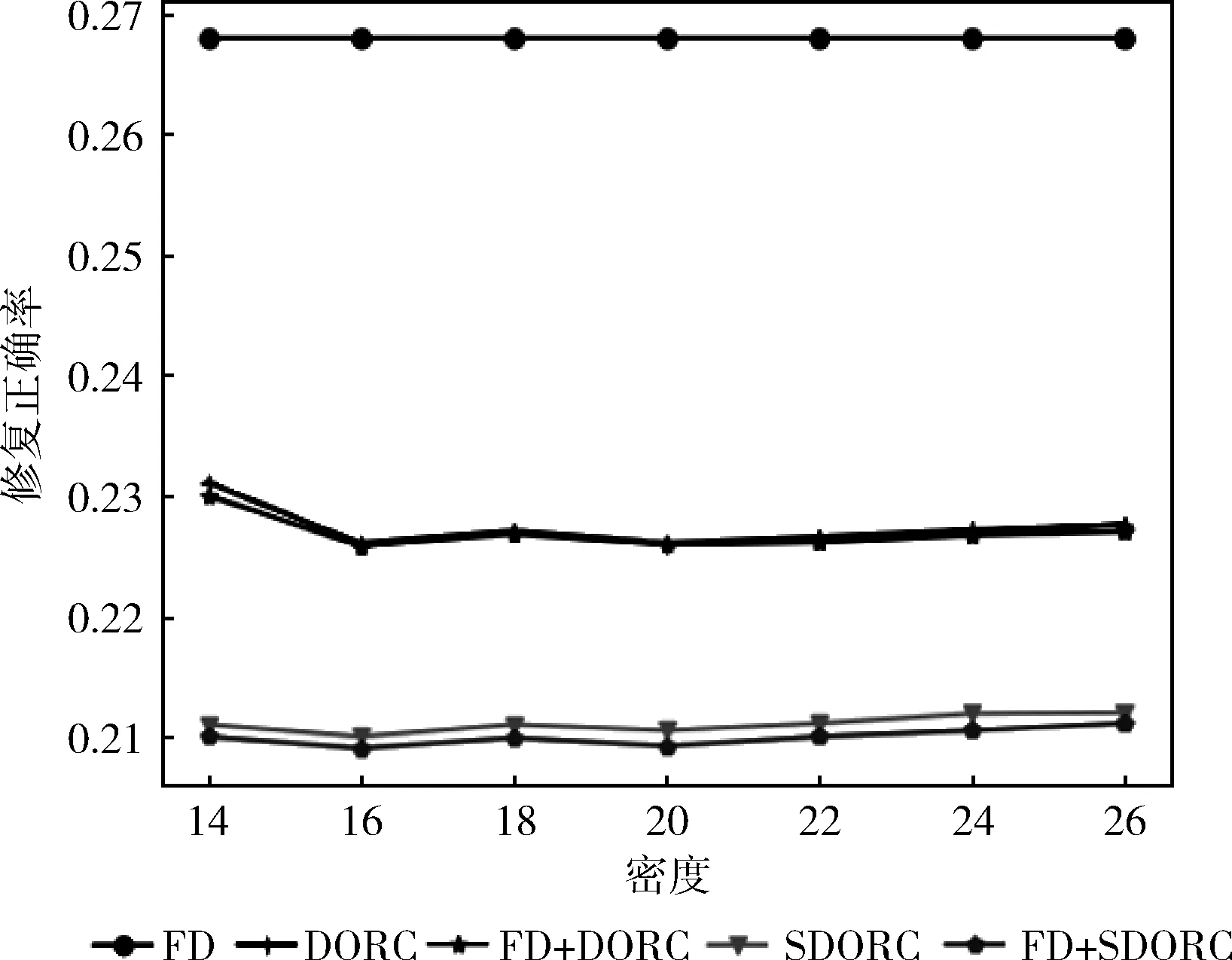
图4 修复正确率VS密度阈值

由上面4幅图可以看出，SDORC算法相比其它算法在聚类精度和修复正确率上都有提高，先使用现有修复算法再使用本算法聚类精度和修复精度都有提高，验证该算法是现有修复算法的扩展。

3.3 UCI数据集实验结果及其分析

为了验证算法在真实数据集上的可行性，采用来自UCI上的4个真实数据集(见表3)，实验以Windows7，Python为实验环境。在确定密度阈值和距离阈值情况下随机选取成对约束，对数据集进行10次实验，取10次实验结果平均值作为最终结果。在0.1脏数据率下聚类精度对比见表4。由表4可知，本文算法的聚类精度相比其它现有算法有了一定程度的提升。

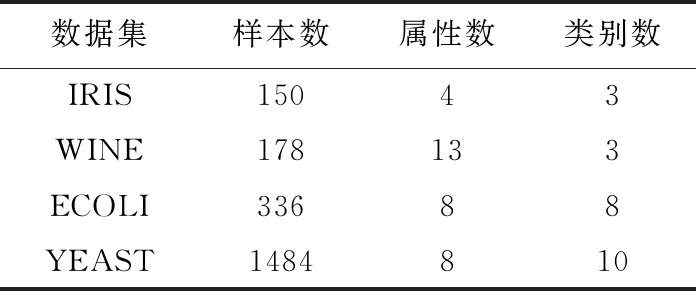
表3 UCI数据集

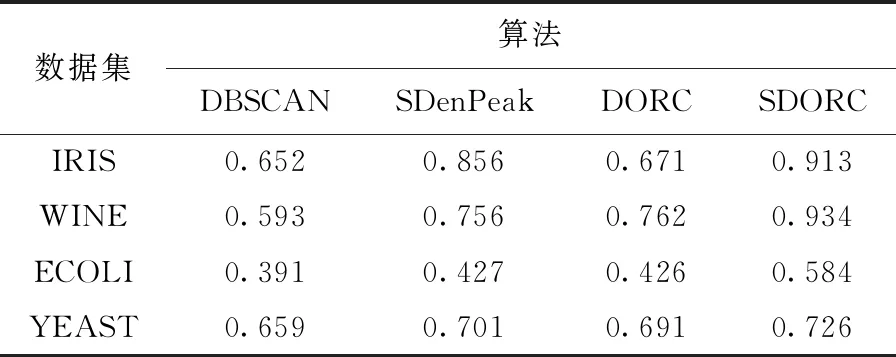
表4 聚类精度对比

4 结束语

现有的密度聚类对于脏数据的处理是简单丢弃，在丢弃的同时也损失了数据集本身的信息；现有的数据修复算法都是基于函数依赖等一些依赖关系对关系型数据库进行数据修复，但是依赖关系的获得要求对数据集要较好的理解，而且不适用于没有函数依赖的简单数据集。本文提出的算法充分利用数据的密度信息，将密度聚类和数据修复相结合，加入了半监督信息(成对约束信息)提出了SDORC算法，该算法适用于简单数据集，是现有修复算法的扩展。实验结果表明,该算法有效提高了数据集的聚类精度和修复正确率。本文采用的成对约束是随机选取的，如何选择较好的成对约束以提高聚类和修复精度，将是进一步探讨的问题。