构建以G(nλ1/xλ2)(λ1λ2>0)为核的半离散Hilbert型不等式的充要条件及应用

洪 勇, 曾志红

(1.广东白云学院 数学教研室, 广州 510450; 2.广东第二师范学院 学报编辑部, 广州 510303)

1 引言与预备知识

(1)

称为半离散Hilbert型不等式, 其中:

K(n,x)称为不等式的核.

若K(n,x)=G(nλ1/xλ2), 则K(n,x)是一种非齐次函数, 并显然满足： 对t>0, 有

K(tn,x)=K(n,t-λ1/λ2x),K(n,tx)=K(t-λ2/λ1n,x).

(2)

本文在λ1λ2>0的条件下, 研究以K(n,x)=G(nλ1/xλ2)为核的式(1)成立的参数条件及最佳常数因子问题, 这类问题对讨论l空间与L空间之间的奇异积分算子及级数算子的有界性与算子范数有重要意义[1-10].

则有λ1W2(α,p)=λ2W1(β,q), 且

于是λ1W2(α,p)=λ2W1(β,q),

根据K(t,1)t-(α+1)/p+c在(0,+∞)的递减性, 类似可得

2 构建半离散Hilbert型不等式的充要条件及最佳常数因子

1) 当且仅当c≥0时, 存在M>0, 使得

(3)

2) 当c=0时, 式(3)的最佳常数因子为

an=n(-α-1-|λ1|ε)/p,n=1,2,…

(4)

则有

又由于K(t,1)t-(α+1)/p在(0,+∞)上递减, 有

从而

(5)

反之设c≥0, 根据混合型Hölder不等式、Lebesgue逐项积分定理及引理1, 有

取M=(λ2/λ1)1/qW1(β,q)可得式(3).

则计算可得

同时, 又有

综上可得

从而

令ε→0+, 利用Fatu引理, 得

再令δ→0+, 得

3 应 用

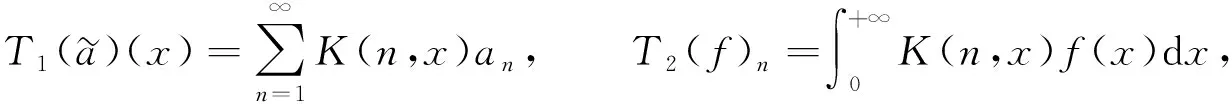
(6)

则其可实现l空间与L空间的映射.根据Hilbert型不等式的基本理论, 式(3)可等价地写为以下两种形式：

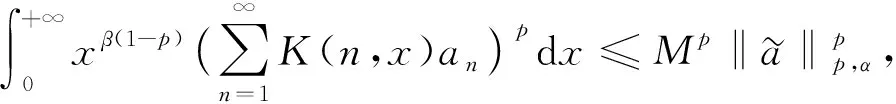
(7)

(8)

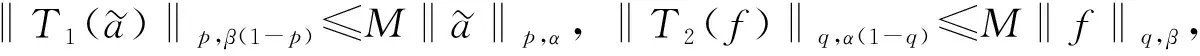
收敛.则下列结论成立:

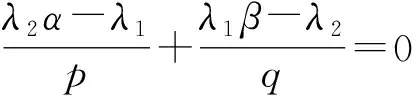
其中B(u,v)是Beta函数.

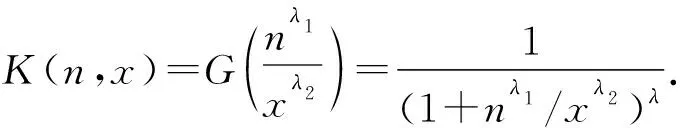
综上并根据定理2, 可知推论1成立.

在推论1中, 取λ=λ1=λ2=1,p=q=2, 则可得：

推论2设-1<α<1, 1<β<3,α+β=2, 算子T1和T2定义分别为