为“错”说理

郜舒竹

【摘   要】以学习活动为中心的数学教学，必然会面对学生个性化的生成，这样的生成具有多样性和差异性，自然也会有错误。因此，如何面对这样的生成，对教师来说是一种挑战。基本观点是：生成是创新，生成必多样，生成是财富;错误是必然的，错误是普遍的，错误是有理的，错误是有用的。为错误找到理由，使之成为教学资源，是教学研究的重要课题。

【关键词】錯误;生成;异样生成

在某培训机构的网络课程中，看到一个一年级小学生的错题讲解。题目是：“小猴子说：我吃了3个桃子，还剩下4个桃子，原来有多少个桃子？”学生的答案为：7-3=4（个）（如图1）。

教师讲解的大意是，这样列式计算是错误的，正确答案应当是“3+4=7（个）”。此类“加减混淆”的现象在低年级学生中极其普遍，这是不同于教师预设的生成，不妨叫作“异样生成”。如今的教学倡导“变教为学”，将以教师教的活动为主的课堂教学，改变为以学生学习活动为主的课堂教学。主旨是“育人为本，活动中心，多样生成”。育人为本是实施教学的指导思想，活动中心是践行指导思想的途径与方法，多样生成是活动中心教学必然的结果。多样生成自然包括异样生成，教师在“变教为学”教学改革中面临的一个挑战，就是如何面对异样生成。

一、如何看待异样生成

面对学生的异样生成，教师如果采用“是非分明”的态度，将不同于标准答案的生成一律视为“错误”，归因为学生“没学好、不认真听讲”或“粗心、马虎、不认真”，简单地让学生对照标准答案改错，在学生面前表现出“愤怒+指责+厌恶”，那么带给学生的自然是“恐惧+盲从+气馁”的负面效应。

学生学习过程中出现不同于预设的异样生成，是正常的，还是反常的？是好事情，还是坏事情？如果把异样生成视为学生经过自主思考产生的独特的、个性的想法，当然就是多样的，符合育人为本、活动中心的教学主旨。因此面对异样生成，包括错误，教师应当采取肯定和接纳的态度，异样生成可以成为研究学生思维规律的“数据（Data）”，进而成为教师的教学资源。这样的教学研究至少应当包括“辨别、解释、应用”三个方面的内容。

所谓“辨别”，就是需要回答“错没错”的问题。错没错的辨别标准，往往会以教科书或教学参考书、命题专家给出的标准答案为参照，简言之就是以成人事先预设为标准，而这样的标准明显具有主观性和局限性。学生的认知是复杂的过程，具有动态的过程性和多样的差异性。错误的答案可能蕴含着合理的思维，错误的过程可能得到正确的结果，独特的生成可能隐藏着创新的思维。因此，辨别错误应当站在学生的立场上，从学生的思维过程中寻找规律，寻找其合理成分。

在辨别的基础上解释学生的生成，指的是需要回答“为什么”的问题。任何事物都有存在的理由，任何现象都有出现的原因。学生的生成是认知过程的结果，这个结果必然与认知过程中的某些规律相关。努力寻找并发现这样的规律，为学生的生成找到原因，对于教师了解学生的学习认知规律，提升教学水平，无疑是重要的。

有了相对准确的辨别和解释，就可以应用生成开展学习活动的教学，让学生的生成包括错误，成为教学资源。让学生之间有机会交流、分享，让学生有机会自我反思，让学生能够在反思、交流中自我评价、自我否定。应当相信：

l生成是创新

l生成必多样

l生成是财富

二、“错误”的合理性

人的认知活动通常体现为三个方面：第一是对情境的感知;第二是在感知过程中头脑中无意识的判断;第三是符号表征。法国的格拉德·沃格诺德（Gérard Vergnaud）把这样三个方面的综合叫作“理解域（Conceptual Field）”[1]。就是说，感知、思维和表征三个过程并不是依照时间顺序进行的，而是交互着相互影响的。

前面“猴子吃桃”的情境，是在时间、空间和数量三个方面，体现运动与变化的“事件（Event）”。任何事件都有一个从始到终的过程，从时间顺序上涉及三个要素：起始状态、变化过程、终极状态。这三个要素表现在“猴子吃桃”情境中，分别为：

l起始状态：原有桃子

l变化过程：吃掉桃子

l终极状态：还剩桃子

如果把起始状态“原有桃子”的全体视为一个“类”，个别桃子视为“类”中的对象或元素，联系到熟悉的容器思维（容器图式），这个事件在头脑中的意境就成为：

l起始状态：容器中有物品

l变化过程：取出部分物品

l终极状态：还剩部分物品

应用格拉德·沃格诺德所说的理解域，头脑中会无意识地形成如下判断，容器中的物品数量：

l放入会增加

l取出会减少

“放入会增加”指的是起始状态和终极状态之间的数量关系，也就是如果变化过程是向容器中放入物品，那么终极状态的数量应当多于起始状态的数量。反过来说，起始状态的数量应当少于终极状态的数量。同样，“取出会减少”指的是终极状态的数量应当少于起始状态的数量，或起始状态的数量应当多于终极状态的数量。

格拉德·沃格诺德把这样在情境感知中，不知不觉的判断，叫作“行动中的定理（Theorem in Action）”，是支配后续行为的重要因素。头脑中形成了这种判断，接下来是用符号表征这样的事件。延续前面“放入会增加、取出会减少”的判断，自然推理出新的判断：

l增加应当用“加”

l减少应当用“减”

“猴子吃桃”事件与“从容器中取出”相对应，头脑中起支配作用的判断自然是容器中数量减少，减少应当用减法。这样的思维过程自然就会导致“7-3=4”的符号表征。

另外，用算式表征情境，相当于涉身认知中的“隐喻（Metaphor）”，指的是不同领域之间的“对应（Mapping）”，也可以认为是“类比（Analogy）”推理。这样的对应通常会遵循“同构（Isomorphism）”的对应原则（同构就是结构相同的意思），表现为三个方面的“一一对应（One-One Mapping）”：

l对象与对象对应

l动作与动作对应

l关系与关系对应

“猴子吃桃”情境中，“桃子”与“数”的对应可以认为是对象与对象的对应，“吃了”与“减”的对应是动作与动作的对应，情境中的时间顺序与符号表征从左到右的顺序保持一致，可以认为是关系与关系的对应。具体表现为，起始状态的“原有”与“被减数”对应，“吃了的桃子”与“减数”对应，终极状态的“还剩”与“差”对应，保持了事件“发生—发展—结束”的时间顺序，与算式中被减数、减号、减数、差从左向右的空间位置关系保持一致。这种在隐喻映射中保持不变的内容，在认知科学中叫作“不变量（Invariance 或 Uniformities）”[2]。

[事件 起始状态 变化过程 终极状态 猴子吃桃 原有 吃了 还剩 容器 原有 取出 还剩 算式 7 -3 =4 ]

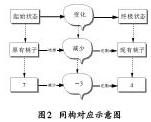
因此，这个对应完全符合“对象与对象、属性与属性、关系与关系”的同构原则。学生对于“猴子吃桃”问题列出算式“7-3=4”，符合涉身认知中隐喻思维规律。从时间顺序上说，是从起始开始，经历变化，到终极结束;从属性上说，是从多到少的变化过程;从事件发生、发展上说，是从开始到结束。可以用图2直观表示这样的隐喻过程。

像这样同构对应的思维方式，在语言转换或互译中也很普遍。比如英语学习中“Nice to meet you”这句话，对于母语为汉语的中国人不会感觉困难，因为它与汉语“很高兴见到你”的字词及其顺序基本相同，也即英语表达与汉语表达相互之间的对应符合同构原则（如图3）。

中文的“谢谢你”转换为英文“Thank you”，如果“谢谢”对应“Thank”，“你”对应“You”，同样具有同构的对应，也很容易理解。反过来，中文中回应感谢时常说“不用谢”，在英文中就不存在具有同构对应的说法，回应“Thank you”时，不能说“Not thank”或“No thanks”。说法可能是“You are welcome”“Its okey”“No problem”。

这些说法都无法与“不用谢”建立同构对应，自然就会成为英语学习的难点。因此可以说，同构对应思维会成为违背同构关系对象认知的障碍。这也就解释了在“猴子吃桃”情境中，为什么学生对“3+4=7”难以接受，原因就在于算式“3+4=7”，破坏了从情境到算式的同构对应。元素之间的对应，打乱了时间顺序关系以及数量增加、减少的属性变化规律（如图4）。

三、互逆关系

接下来的问题是，如何将算式“3+4=7”与“猴子吃桃”情境之间建立起合乎思维规律的联系？原题事件整个过程是由于“吃掉”，从而“减少”的过程，与符号表征“7-3=4”具有同构对应关系。而“3+4=7”需要想象反过来的过程，也即“补回”，进而“增加”的过程（如图5）。

这个反过来的过程在“猴子吃桃”事件中并未发生，属于“虚构（Fictive）”的事件，具有“想象（Imaginary）”的特征，把想象的过程用算式描述出来，实际是两步计算：

7-3+3

=4+3

=7

第一步“7-3=4”对应“吃掉”或“减少”3个，还剩4个;第二步“4+3”对应“补回”或“增加”3个，得到原有桃子数量。这样的过程，对于一年级学生显然具有难以理解的复杂性。加与减作为运算的“互逆（Inversion）”关系，需要许多涉身活动经验的积累才有可能逐步理解。比如：

l前进10步后，倒退10步，回到原地。“前进”与“倒退”具有互逆关系。

l上学是从家到学校，下学就是原路返回，回到家中。“上学”与“下学”具有互逆关系。

l收拾书包准备上学是向书包中放入书本，到学校准备上课，从书包中取出书本。“放入”与“取出”具有互逆关系。

l工资的“收入”与消费的“支出”，具有互逆关系。

诸如此类的涉身活动，都可以成为隐喻加、减运算互逆关系的涉身经验。这种“增”与“减”的互逆关系，是沟通这两个运算联系的基本规律。数学家建构代数结构时，运算的互逆关系起着基础性的重要作用。

四、预见错误

通过解释学生的异样生成，可以帮助教师预测学生的认知困难以及可能出现的错误。以上案例分析可以得到一个结论：凡违背隐喻同构对应的现象，学生都会出现类似的理解困难，进而写出与教师期望不同的算式。將“猴子吃桃”推广到一般的事件，其基本结构可以用图6表示。

从时间顺序关系上看，分别为起始状态在“前”，变化过程在“中”，终极状态在“后”。事件发生、发展的顺序遵从“从前到中”和“从中到后”规律。学生熟悉的问题自然是符合事件发生发展顺序的“知前想后”（如图7）：已知有7个桃子，小猴子吃了3个，还剩几个？可以轻易得到“7-3=4”的算式。

前面“猴子吃桃”问题之所以难，是已知“中、后”，求“前”（如图8）。

这相当于时间倒流，与学生熟悉的“知前想后”顺序相悖。如果题目更改为：有7个桃子，小猴子吃了一些，还剩4个，问小猴子吃了几个？信息结构为已知“前、后”，求“中”，同样破坏了事件的时间顺序（如图9）。

可以预测，一定会有学生写出“7-3=4”的算式，而不是期望的“7-4=3”。原因就在于按照从左到右的顺序看，“7-3=4”符合题目叙述事件的顺序。有了这样的理解，就不难预测下面几个问题对于学生的难易程度，以及可能出现的异样生成。

l小明有5块巧克力，需要增加多少块，才能拥有8块巧克力？

l小明有8块巧克力，给了小红一些后还剩5块。小明给了小红多少块巧克力？

l小明有8块巧克力，给了小红3块。小明还剩多少块巧克力？

l小明有一些巧克力，小红给了小明3块后，小明共有8块。小明最初有多少块巧克力？

五、情境与语言的复杂性

与自然数加、减运算相关的问题类型，除了前面的“事件”类型之外，典型的还有“局部—整体（Part—Whole）”以及“比较（Comparing）”。“局部—整体”结构的问题通常包括一个整体和两个局部，其基本关系可以用图10示意。

如果已知两个局部的数量，则运用加法可以计算出整体的数量。与之对应的减法问题就是知道整体和一个局部的数量，求另外一个局部的数量（如图11）。

用文字叙述这个问题可以是：小明有8块巧克力，5块是黑色的，其余是白色的。他有多少块白色的巧克力？

这种整体与局部关系的情境不涉及空间位置和时间顺序的变化，从结构上看相对单一。较为复杂且对于低龄学生不易理解的类型，是不同对象间进行比较与变换的数量关系，以及前面介绍的事件中运动与变化的类型。[3]会出现同样的算式对应不同的情境，以及同样的情境对应不同的语言表述的情况，表现出语言表述与情境的多样性和复杂性。

比较关系的故事情境需要有两个对象，各自的数量不同，因此就会出现“多多少”或者“少多少”的问题。比如对于“5+3=？”这样一个算式，可以对应下面不同的语言表征。

l小红有5块巧克力，小明比小红多3块。小明有多少块巧克力？

l小红有5块巧克力，如果小明减少3块就和小红一样多。小明有多少块巧克力？

还可以交换主语和宾语的位置叙述为：

l小红有5块巧克力，比小明少3块。小明有多少块巧克力？

l小红有5块巧克力，如果小红再增加3块就和小明一样多。小明有多少块巧克力？

利用加法和减法的互逆关系，从这些加法算式的情境，还可以衍生出用减法算式计算的情境。

l小明有8块巧克力，小红有5块巧克力。小明比小红多多少块巧克力？

l小明有8块巧克力，小红有5块巧克力。小明减少多少块就和小红一样多？

l小明有8块巧克力，小红有5块巧克力。小红比小明少多少块巧克力？

l小明有8块巧克力，小红有5块巧克力。小红需要得到多少块巧克力才能和小明一样多？

l小明有8块巧克力，如果小红再得到3块就和小明一样多。小红有多少块巧克力？

l小明有8块巧克力，如果减少3块就和小红一样多。小红有多少块巧克力？

表面看都是相同的情境，但由于语言表述以及顺序差异，会给学生带来不同的认知困难。因此“运算”作为一类数学学习活动，是多元的、复杂的。计算教学仅限于针对算式的算法和算理是远远不够的。把计算拓展为运算，把运算与涉身认知活动联系起来，实质是“情境、判断、符号”之间的互动过程。

在这样的过程中，学生会出现多样的生成，包括错误。教师应本着“育人为本”的指导思想，秉承“错误是必然的，错误是普遍的，错误是有理的，错误是有用的”信念，用宽容、接纳和研究的态度面对学生的异样生成和错误。

应当承认，我国社会目前对于基础教育中的学科教学的认识仍然囿于“应试”思维，“办老百姓满意的教育”就成为顺应这种思维的教育。评价学校教育质量看分数，评价教师教学质量看分数，教学“质量”的高低与“分数”的高低成了正比例关系。

在这样的现实中，家长、教师厌恶学生的“错”，是顺理成章的，因为“错”是“低分”的根源。因此，教学的改变需要时间，需要政府管理和评价的改变，需要家长乃至社会观念的改变，需要学校教学管理的改变，由此才有可能带来教师教学真正的改变。

作为最基层、最普通的教师，不妨从“收集、解释、应用”学生错误入手，让“错”发挥教学资源的作用，这样的做法或许会获得“素质教育”与“应试教育”的双丰收。

参考文献：

[1]VERGNAUD G. Cognitive and Developmental Psychology and Research in Mathematics Education： Some Theoretical and Methodological Issues[J]. For the Learning of Mathematics， 1982， 3（2） ： 31-41.

[2]LAKOFF G. Women， Fire， and Dangerous Things. What Categories Reveal about the Mind[M]. Chicago： The University of Chicago Press， 1987： 211.

[3]ROMBERG， COLLIS， GROUWS. Learning to Add and Subtract[J]. Journal for Research in Mathematics Education， 1987（2）.

（首都師范大学初等教育学院   100048）