最值问题有法可依基本图形彰显魅力
——“最短路径问题”在几何解题中的应用

广东省东莞市东华初级中学(523128) 胡厚伟

现实生活中经常遇到最短路径问题,数学史中的“将军饮马”就是最典型的最短路径问题之一.初中阶段主要以“两点之间,线段最短”“垂线段最短”为基础知识,借助于轴对称、三角形三边关系、平移变换、数形结合与转化思想进行研究.此类问题只要抓住基本图形,牢牢的抓住这一神器不放手,以不变应万变,几何中的最值问题就迎刃而解.下面,笔者以八年级上册“最短路径问题”为例,谈谈基本图形在几何解题中的魅力所在.

1 典故引入孕育几何的基本图形

情境描述“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗.而由此却引申出一系列非常有趣的数学问题,通常称之为“将军饮马”.这个问题可描述为:如图1,将军从军营A出发先到河边饮马,然后去同侧的B地开会,问:将军应该怎样走才能使路程最短?

图1

图2

分析说明对于八年级的学生而言,“将军饮马”这个典故小学就已经接触过,但小学的老师只是把这个典故讲给学生听,并没有给学生讲明白这个典故中所蕴含的基本原理,涉及到的知识和方法.在日常教学中,以学生非常熟悉的典故引入新课,可以激发学生探究新知的欲望,培养学生学习数学的兴趣.将生活中的“将军饮马”问题抽象为“如图2,在直线l上找一点P使得PA+PB之和最小?”的几何最值问题,然后用相关数学知识来解决问题.

2 提炼图形理清知识的来龙去脉

基本图形A、B两点在直线MN的两侧(如图3)或同侧(如图4)时,基于“两点之间,线段最短”为基础知识,解决求AP+BP之和的最小值问题.

图3

图4

原理说明基本图形源自于人教版七年级上册教材第129 页,当时的学习并没去进行验证,只是经过测量验证、经验总结直接得到一个基本事实:两点的所有连线中,线段最短.简单说成:两点之间,线段最短.学完八年级上册三角形三边关系、轴对称等知识后,证明这个基本事实就显得非常容易.

如图3,定点在直线MN两侧.连接AB交直线MN于点P,则AP+BP最小.理由:在直线MN上任意取一点P′,连接AP′,BP′,构成ΔAP′B,由三角形任意两边之和大于第三边的关系可得AP′+BP′＞AB(即AP′+BP′＞AP+BP),则AP+BP之和最小.

如图4,定点在直线MN同侧.作点B关于直线MN的对称点B′,连接B′A交直线MN于点P,则AP+BP最小.由轴对称的性质可知,直线MN是线段BB′的垂直平分线,则PB=PB′,所以AP+PB=AP+PB′,即AP+PB=AB′,运用化“折”为“直”的方法将AP+PB最小的问题转化为线段AB′最小的问题,后同“两点在直线MN的两侧”的说理过程.当然,也可选择作点A的对称点,也可得到证明.不管选择哪个点去作对称点解决此问题,点P的位置始终不会改变.

3 变换背景提升图形的应用能力

3.1 以三角形的相关知识为背景

如图5,等边ΔABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=3,EM+CM的最小值为_____.

图5

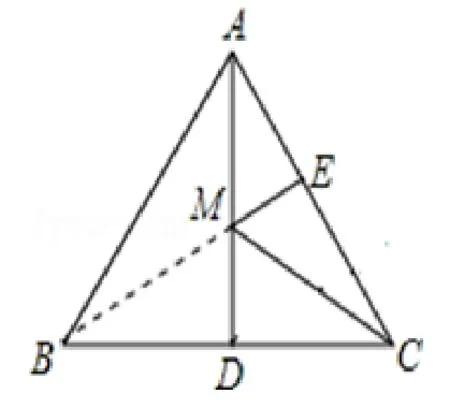
图6

解析等边三角形的对称轴是中线AD所在的直线,利用它进行转换.如图6,点B关于直线AD的对称点C,连接BE交AD于点M,则BM=CM.可将求EM+CM的最小值转化为BM+EM的最小值,即BE的最小值.因为AC=6,AE=3,所以CE=AE=3,即E是AC的中点,由等边三角形三线合一的性质可得BE⊥AC,由勾股定理可得即EM+CM的最小值为

3.2 以四边形的相关知识为背景

如图7,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值为_____.

图7

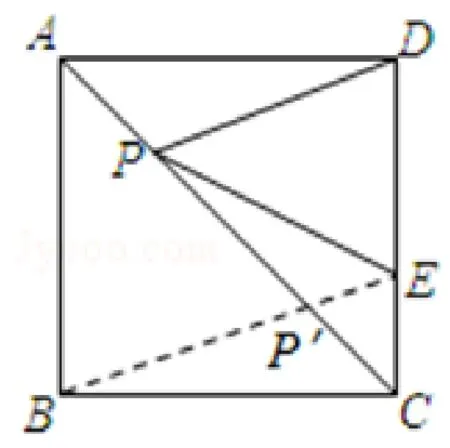
图8

解析正方形是轴对称图形,有4 条对称轴,本题的对角线AC所在直线就是其中一条对称轴,可利用它进行转换.如图8,由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PE+PD=BE最小,而BE是RtΔCBE的斜边,再由勾股定理即可得出PE+PD的最小值为

3.3 以圆的相关知识为背景

如图9,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为____.

解析⊙O两个点A、B在直径MN的同侧,圆是轴对称图形,对称轴为直径所在的直线.如图10,过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B的长度为PA+PB的最小值,可得弧AN等于弧A′N,由圆周角定理可求出∠A′ON=80°,∠BON=40°,可得∠A′OB=120°,因为O′A=OB,所以∠OA′Q=∠OBQ=30°,然后过O作OQ⊥A′B于Q,在RtΔA′OQ中,OA′=2,可求出A′B=2A′Q=即PA+PB的最小值

图9

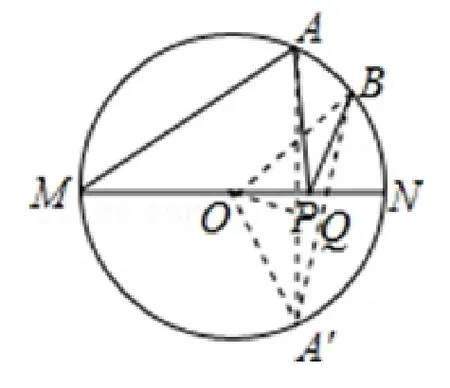
图10

点评三个问题通过不同的背景,结合相关知识,通过勾股定理求出所需数值,找准了两点一线,基本图形就成为了常见的图形.不管在什么背景下,找准对称轴是关键,灵活运用轴对称性质,化“折”为“直”,基本图形都能运用上,将基本图形形式化,不仅锻炼了综合运用知识的能力,运用基本图形的过程中体会数学的转化思想,学会用已有知识解决未知问题.

4 回归生活培养学生的学习兴趣

4.1 将军饮马型问题

如图11,斯诺克比赛桌面AB宽1.78m,白球P距AD边0.22m,距CD边1.4m,有一颗红球Q紧贴BC边,且距离CD边0.1m,若要使白球P经过边AD、DC,两次反弹击中红球Q,求白球P运动路线的总长度.

图11

图12

解析点P和点Q是两定点,两次反弹的具体点未知,但可由前面做题经验得出结论.如图12,由题意可知PH=0.22m,MC=1.4m,QC=0.1m.作点P关于AD边的对称点P′,点Q关于CD边的对称点Q′,连接P′Q′交AD于点E,交CD于点F,则运动路线长为PE+EF+QF的长度之和,即P′Q′的长.然后延长PP′交BC于点M,易知P′H=PH=0.22m,CQ=CQ′=0.1m,则P′M=P′H+HM=1.78+0.22=2m,MQ′=MC+CQ′=1.5m,在RtΔP′MQ′中,由勾股定理可知P′Q′=2.5m,即白球P运动路线的总长度为2.5m.

4.2 造桥选址问题

如图13,A和B两地在一条河的丙岸,现在要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)

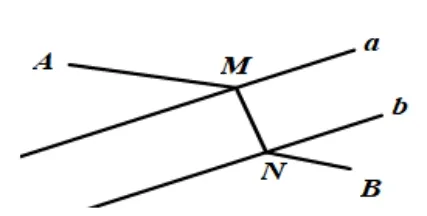
图13

图14

解析由于河岸宽度是固定的(即桥长为定值),因此当AM+NB最小时,AM+MN+NB最小.这样,问题进一步转化为:当点N在直线b的什么位置时,AM+NB最小?可将AM沿着与河岸垂直的方向进行平移,点M移动到点N的位置,点A移动到点A′的位置,则AA′=MN,AM+NB=A′N+NB.此时,问题转化为在直线b上的找一点N′到A′、B的路径之和最短,即转化为定点A′到定点B的最短路径.连接A′、B两点的线段中,线段A′B最短.因此,线段A′B与直线b的交点N的位置即为所求,即在点N处造桥MN,所得路径AMNB是最短的.这个问题的关键是定长线段MN把动线段分隔,此时须通过平移把动线段A′N、BN变为连续路径,此题也可将BN向上平移MN的长度与点A连接.

点评数学来源于生活,又用于生活,同时又运用于社会的每一个角落.将军饮马问题和造桥选址问题是典型的生活问题,在此选取的将军饮马问题属于两定两动型的几何问题抽象而来,找两定点的对称点再连线即可得到答案.而桥选址问题属于平移变换型,此类问题当动折线被定长线段分散时需化为连续折线,一般用平移变换的方法去构造,然后利用“两点之间,线段最短”的知识去解决问题.

5 结束语

在最值问题的学习过程中,引导学生将前后所学知识进行串联,形成完备的知识体系,将解题过程中用得较多的重要结论(两点之间线段最短、三角形两边之和大于第三边、两边只差小于第三边、垂线段最短等)及常用方法(路径成最短,折线到直线;同侧变异侧,分散化连续.)进行归纳总结.引导学生抓住基本图形,用好轴对称性质,数形结合、转化思想方法,通过基本图形不断深化从而学会解决综合性的问题.数学来源于生活,但又高于生活.从生活中抽象出数学基本图形,又将基本图形生活化,从而达到数学学习的目的,提升学生的基本能力,落实数学核心素养.