借助GeoGebra软件化解受力分析抽象问题
周忠仁
摘 要:本文借助GeoGebra软件动态呈现受力分析的抽象问题,以两个具体问题为例,分析学生学习过程存在的困惑、困惑成因,及解决对策,并借助软件,制作针对性的模拟动画,对抽象问题进行直观形象地展示,给学生良好的视觉体验,提升教学效果。
关键词:GeoGebra;受力分析;晾衣服;物理模型
受力分析是高中力学的基础,也是处理电学、磁学中力学问题的重要前提,是学生在中学物理学习阶段所必需掌握的技能。但“力”是一抽像概念,既看不见,也摸不着,在学习过程中,学生头脑中己有的生活经验常常对这一知识点的学习构成障碍,对物理模型的构建存在消极影响,学习过程存在观念转变的困难。借助GeoGebr软件,将抽象的力问题直观、生动的反映出来,对学生易错的受力分析实例进行模拟与拓展,让学生经历物理模型的建构过程,有助于学生头脑中物理模型的构建,能有效帮助学生处理受力分析的抽象问题。
1 GeoGebra简介
GeoGebra软件是一款教学辅助能力强于几何画板的动态数学软件,数形结合能力突出,能让抽象的物理问题,转化为直观、生动的动态图形。软件演示方便,开源、免费且可跨平台使用,非常适合于数学与物理课堂的教学演示,便于加深学生对知识点的理解与掌握,有利于学生思维的发展。下文是笔者将GeoGebra软件应用到力学课堂中,化解学生学习困难,促进教学效率进行的思考与尝试。
2 用GeoGebra辅助受力分析的教学
2.1 题目展示
【例题1】如图1,与三角形斜面体A相似的B叠放在A的上方,且与左侧粗糙墙壁接触,A的底部有一竖直向上的外力F,若在F作用下A、B处于静止状态,则关于A和B受力情况的描述,正确的是( )
A.除力F外,A一定还受到三个力
B.B可能受到四个力
C.B一定受到墙壁对它向右的弹力
D.B对A的摩擦力沿接触面向上
2.2 问题的题出
学生困惑:整体法与隔离法是受力分析中常用的重要方法[ 1 ],本題分析思路是先以A、B整体为研究对象,确定B物体与墙之间一定没有弹力和摩擦力,再隔离B物体,确定B物体的受力情况,也就能确定A物体的受力情况,得到本题正确答案A,上述分析思路清晰、明了。但在教学中常发现很大一部分学生对B物体的受力情况存在困惑如下:放在A物体上的B物体,会下滑挤压左侧墙壁,墙壁对B物体应有一个向右的弹力。
困惑成因:按生活经验:“大块头”B物体较重,无法在摩擦力的作用下停在“小块头”A物体上,故墙壁与B物体之间存在挤压。在有此观念的同学头脑中,固执的认为:没有墙壁的情况下:①若B物体形状大→质量大→会下滑→不可能静止;②若B物体形状小→质量小→有可能静止。究其原因,是这部分同学头脑中片面的生活经验,对此内容的学习存在消极影响,学习过程存在观念转变的困难。
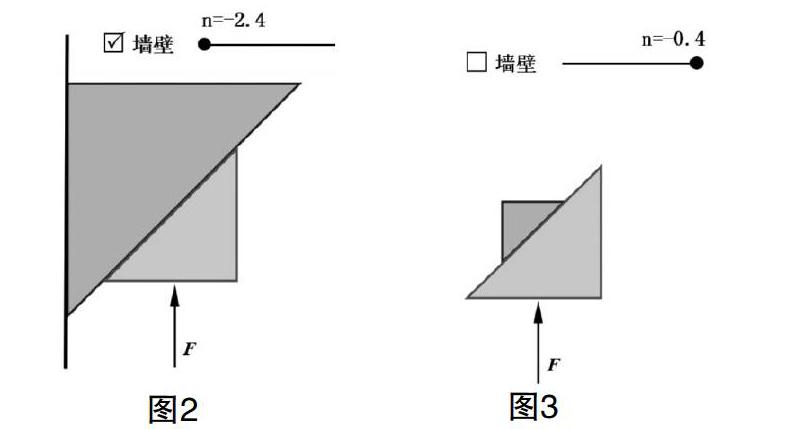
解决对策:借助同学们头脑中固执的生活经验,设法消除其头脑中观念①的不利影响,保留头脑中观念②的积极影响,使其对该知识点的学习产生正迁移作用。具体做法:先借助GeoGebra软件模拟题目中的物理情境如图2,然后隐藏墙壁,再控制B物体的大小,使其变成图3的情境,在此基础上,教师再加以引导,学生容易明白:原来他们头脑中的观念①和观念②是同一个物理情境。上述处理过程能有效的转变了学生头脑中的错误观念,利用前概念的积极影响,帮助学生完成概念的同化。
2.3 GeoGebra模拟作图
制图步骤:
(1)描点A(0,0)、B(3,0)、C(3,3),并用多边形工具绘制三角形t1,并填充浅颜色表示三角形滑块m。
(2)添加滑动条,命名为k,用来控制三角形t1的位似三角形t1'的大小,用t1'模拟另一个三角形滑块M的大小,打开“属性”对话框,设置“最小”为-2.4,“最大”为-0.4,增量为0.01。
(3)指令栏输入公式“D=(A+C)/2”,确定线段AC的中点D,用于作为做t1位似三角形的位似中心。
(4)指令栏输入公式“位似(t1,k,D),得到三角形t1',填充浅颜色表示三角形滑块M。
(5)指令栏输入公式“E=(A+B)/2”,确定线段AB的中点,再输入公式“向量〔E-(1.5; π/ 2), E〕”,得到向量u,用于模拟外力F。
(6)描绘线段f,用于模拟墙壁,并用“复选框”控制墙壁的显示与隐藏。
(7)隐藏不必要的点,并做适当的美化。
3 用GeoGebra辅助“晾衣服”模型的教学
3.1 题目展示
“晾衣服”模型是高中物理力学模块中的一个重要模型,近几年高考有多次直接或间接的考查,该模型是多个力学重要知识的组合应用,涉及三力平衡的对称模型、力的动态平衡问题等重要知识,同时也对学生构建物理模型,解决实际问题能力有较高的要求。在教学中,常发现学生对涉及该模型的题目存在思维困惑。
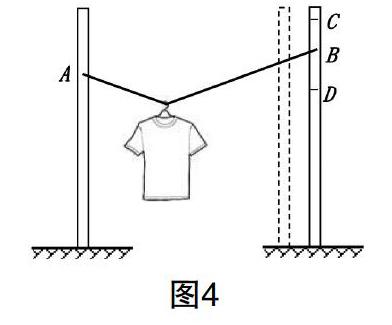
【例题2】如图4所示,两根竖直杆间有一光滑轻绳AB,悬挂衣服的晾衣架可在轻绳上自由滑动,在无风的情况下衣服处于静止状态。现让绳子左侧A端不动,将右侧B端移动到一个新的位置,稳定后,关于绳子张力的说法正确的是( )
A.竖直杆不动,将绳子B端向上移到C位置时,绳子张力不变
B.竖直杆不动,将绳子B端向下移到D位置时,绳子张力变小
C.绳子B端随杆向左移到虚线位置时,绳子张力变大
D.绳子B端随杆向左移到虚线位置时,绳子张力不变
3.2 问题的提出
学生困惑:本题分析思路是以悬挂点为研究对象,因绳子没有打结,两边绳的张力FT相等,又两绳在水平方向分力相等,故两边绳的张力关于过悬挂点的竖直线对称,设绳与坚直线的夹角为θ,由对称性可得G=2FTcosθ,再设绳长为L,A、B两端点在水平方向上的间距d,由几何关系得sinθ=,到此可求得本题绳子张力只与d有关,可得答案:A。上述分析思路,对头脑中能正确建立对称模型的同学来说,清晰、明了。但在教学中,常发现很大一部分学生对“两边绳的张力关于过悬挂点的竖直线对称”这一结论存在困惑如下:①左右绳子长度明显不同,怎么会关于过悬挂点的竖直线对称?②就算移动前两边绳的张力对称,现移动B点,两边夹角应该都发生了变化且不再相等了呀。
困惑成因:有以上困惑的学生头脑中,解决力学问题大多缺少了一个重要环节——受力分析,他们头脑中的第一反应不以受力图说话,而是喜欢以生活经验,想当然的认为:左、右两侧绳长不同,则两侧绳张力不同。同时没有抓住题中理想化条件——光滑,而是按生活经验:上下移动B点,两侧绳子都会偏离原位置,则两边夹角都发生了变化且不再相等。
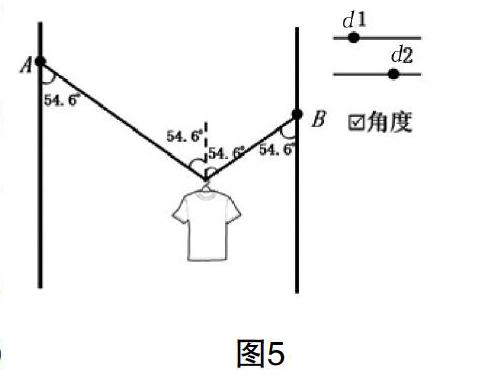
解决对策:为帮助这些同学在头脑中建立该模型,有同行教师做了模拟演示实验,但由于较难得到理想化的光滑条件,该模拟演示实验较难达到理想效果。若在模拟演示后,再借助GeoGebra軟件模拟题目中的物理情境如图5,通过改变B点上下位置和支撑杆左右位置,让学生观察挂钩移动情况,及两侧绳与竖直线夹角的大小关系。在教师定性分析及软件直观演示的结合下,学生一定可以解除心中困惑,完成该模型的建立。
3.3 GeoGebra模拟作图
制图步骤:
(1)添加两滑动条,命名为d1、d2,用来控制左、右两侧支撑杆的水平位置,从而控制两支撑杆间的间距,打开“属性”对话框,对d1设置“最小”为1,“最大”为5,增量为0.01,对d2设置“最小”为6,“最大”为10,增量为0.01。
(2)描出4个点A1(d1,-10)、A2(d1,10)、B1(d2,-10)、B2(d2,10),做线段A1A2、B1B2用于模拟左右两支撑杆,并在两线段上分别描点C、D,做线段A2C、B2D,并在线段A2C、B2D上描点A、B,用于控制晾衣绳两端点位置及在杆上移动的范围。
(3)指令栏输入“L=10”,设置绳长为10,先后以A、B为圆心,L为半径画圆,得到圆与线段A1A2、B1B2的交点G、E。
(4)指令栏输入公式“O=交点〔直线(A, G), 直线(B, E)〕”,做线段AO、BO,模拟左右两段轻绳。
(5)插入衣服图片,设置参数,使得图片大小固定,且衣服挂钓位置随O点移动。
(6)用“角度”功能量出两绳与杆、两绳与过O的竖线的夹角。
(7)用“复选框”控制角度的显示与隐藏。
(8)隐藏不必要的点,并做适当的美化。
4 总结
本文对Geogebra软件融入物理课堂教学做了一次有益的尝试,借助GeoGebr软件的动态演示功能,将抽象的力学问题直观、形象的呈现出来,让学生在良好的视觉体验过程中解决头脑中的困惑,建立正确的物理模型,提升了教学效果。高中物理还有很多抽象不易理解的问题,教学中有必要借助软件对其进行动态模拟,这既能降低学习的难度,又能消除学生的思维障碍。同时培养了学生应用数学知识解决物理问题的能力,提高学生的物理核心素养。
参考文献:
[1]袁睿.关于力学受力分析方法的研究[J].考试周刊,2011(13):188-189.

