由箭图诱导的分次Frobenius代数及其扭超势

陈 斌，俞晓岚

(杭州师范大学理学院，浙江 杭州 311121)

0 引言

Frobenius代数与数学的多个分支都有密切的联系,在数学多个领域都有广泛的应用[1].诸如Frobenius代数与拓扑量子场理论的联系,Frobenius代数与Hopf代数、量子Yang-Baxter方程之间的联系等,连通分次Frobenius代数则与非交换投影几何高度相关.

文献[2]提供了一种通过一个扭超势来建构一个连通分次Frobenius代数的具体方法,并重点阐明了只有一个顶点的情形下扭超势与连通分次Frobenius代数的一一对应关系.本文把研究对象从一次生成的连通分次Frobenius代数拓展到由箭图诱导的分次Frobenius代数,并将分次 Frobenius代数从连通的情形推广到非连通的情形中去.

本文首先考虑一类简单的(由箭图诱导的)分次Frobenius代数,通过“非退化的双线性结构”来刻画分次Frobenius代数在箭图上的几何性质.对于由箭图诱导的分次Frobenius代数,本文对偶地考虑它伴随着相应的生成元和Nakayama自同构的余代数,并证明了相应的生成元就是所定义的扭超势.通过详细描述扭超势生成的余代数结构,本文最后证明任意一个路余代数中的扭超势都能构造一个分次Frobenius代数.

1 预备知识

定义1[3]箭图Q指的是由顶点和箭向构成的定向图,其顶点集和箭向集分别记成Q0和Q1.对箭向α,本文用s(α) 和t(α)分别表示α的起点和终点,即s和t可看作由Q1到Q0的映射.一个箭图Q常表示成Q=(Q0,Q1,s,t).若Q0和Q1都是有限的,则称Q为有限箭图.本文讨论的都是有限箭图.

定义2[3]箭图Q中的路p指的是有限序列p=αl…α2α1,其中每个αi都是箭向且t(αi)=s(αi+1),1≤i≤l-1.用|·|度量路p的长度,记为|p|=l; 定义路p的起点为s(p):=s(α1);定义路p的终点为t(p):=t(αl).本文约定顶点i可看作长度为0的路,并记作ei.路p称为有向圈,简称为圈,如果|p|≥1且s(p)=t(p).

定义3[3]一个箭图Q的路代数KQ作为向量空间是以Q中所有的路为基,乘法定义为路的连接,即对于Q中两条路p和q,若p的终点和q的起点不同，定义乘积q·p=0,否则定义乘积q·p为这两条路的连接qp.由此还可定义偏导如下:

定义4[2]域K上的一个有限维代数A是Frobenius代数,当且仅当存在一个非退化的映射σ:A×A→K,满足

∀x,y,z,x1,x2,y1,y2∈A,k∈K,

(1)σ(xy,z)=σ(x,yz)；(2)σ(x1+x2,y)=σ(x1,y)+σ(x2,y)；(3)σ(x,y1+y2)=σ(x,y1)+σ(x,y2)；(4)σ(kx,y)=σ(x,ky)=kσ(x,y).

如果A还满足σ(x,y)=σ(y,x),那么称A为对称代数.

定义5[2]对每一个Frobenius代数,都存在一个K-代数自同构μ:A→A使得

σ(μ(x),y)=σ(y,x),∀x,y∈A.

这个自同构被称为Nakayama自同构.

定义6[2]一个Z-分次代数指的是一个结合代数A可表示成一系列子空间的直和形式,即A=⊕i∈ZAi,且满足对任意的i,j∈Z,Ai·Aj⊆Ai+j.如果一个有限维分次代数A=A0⊕A1⊕…⊕An是Frobenius代数且其Frobenius结构映射σ满足

σ(x,y)=0, ∀x∈Ai,y∈Aj,i+j≠n,

那么A就是一个长度为n的分次Frobenius代数.当分次Frobenius代数是对称代数时则称为分次对称代数.

一个箭图Q的路代数KQ作为向量空间有一个自然的直和分解

KQ=KQ0⊕KQ1⊕KQ2⊕…⊕KQl⊕…,

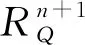
域K上的箭图Q伴有两个向量空间R:=KQ0和V:=KQ1.V是一个R-双模[4],其双模结构RVR有一个自然的直和分解

R上的张量积可由一般的矩阵乘法给出：

其中Bi,k=⊕ei,ek∈Q0Vi,k,Ck,j=⊕ek,ej∈Q0Vk,j.记

其中V0=R.所以,路代数KQ亦可视为张量代数

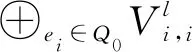
同理,路余代数KQc也有张量表示法KQc=T(V*).对偶地,一个Z-分次余代数意指一个结合余代数C可表成一系列子空间的直和形式,即C=⊕i∈ZCi,且满足对任意的n∈Z,ΔCn⊆⊕i+j=nCi⊗Cj.

定义7[5]弱超势ω指的是路代数KQ中那些同长度成圈的路的线性组合,即：

ω∈KQl,∀ei∈KQ0,ωei=eiω.

弱超势ω为齐次元素,可用齐次分量的长度定义弱超势的长度,沿用度量符号|ω|; 若ωei≠0,则称弱超势ω经过箭图Q中的顶点ei.如果弱超势还满足

定义8[5]弱扭超势ω指的是路(余)代数KQ中那些在一个箭图自同构ι下仍然保持弱超势的几何性质的齐次元素,即

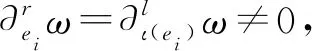
则称它为扭超势.

引理1[6]A是域K上的一个有限维代数,K-对偶空间A*=Hom(A,K)有一个自然的余代数结构.

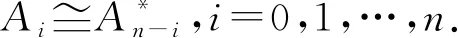
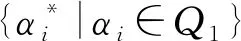
p*q=δp,qs(q),qp*=δp,qt(q), ∀p,q∈KQl.

偏导运算也可对偶表示如下：

路余代数KQc所代表的张量空间T(V*)有相应的余代数结构,其余乘和余单位定义如下：

对单元素ξ∈T(V*),记〈ξ〉为KQc中含有ξ的最小子余代数.

2 一类简单的(由箭图诱导的)分次Frobenius代数

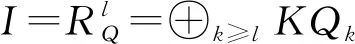
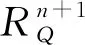
命题1如果KQn是一个分次Frobenius代数,那么对于箭图Q中的每一个顶点ei有且仅有一条以ei为终点的长度为n的路,对于箭图Q中的每一个顶点ej有且仅有一条以ej为起点的长度为n的路.

证明只需考虑其中一种情形即可,先证存在性,再反证唯一性.

考虑σ(ei,-),则对于分次Frobenius形式的映射σ,存在一条长度为n可表示为αinαin-1…αi1的路使得σ(ei,αinαin-1…αi1)≠0.如若不然,那么所有长度为n的路p都使得σ(ei,p)=0.从而对于KQn中的任意一个元素,即任意多条路的线性组合γ,σ(ei,γ)=0:这与σ的非退化性矛盾.已知

σ(ei,αinαin-1…αi1)≠0,

可得

αinαin-1…αi1≠0,t(αi)=s(αi+1),1≤i≤n-1.

又有

σ(ei,αinαin-1…αi1)=σ(1,eiαinαin-1…αi1)≠0,

从而

eiαinαin-1…αi1≠0.

至此即证得

t(αin)=ei.

若对于箭图中的其中一个顶点有不少于两条以它为终点的长度为n的路,则可由KQn的维数等于长度为n的路的条数知

dim(KQn)≥n+1.

根据引理1,

至此

n=dim(KQ0)=dim(KQn)≥n+1,

矛盾已显然.

命题2如果KQn是一个分次Frobenius代数,那么对于箭图Q中的每一个顶点ei有且仅有一个以ei为终点的箭向,对于箭图Q中的每一个顶点ej有且仅有一个以ej为起点的箭向.

证明存在性可由命题1直接得到.

假设有至少两个不同的箭向αi1和αi2以ei为终点,那么根据命题1的存在性,有以s(αi1)为终点的一条长度为n的路αjnαjn-1…αj1和 以s(αi2)为终点的一条长度为n的路αknαkn-1…αk1.于是分别有αi1αjnαjn-1…αj2和αi2αknαkn-1…αk2两条 以ei为终点的长度为n的路,与命题1的唯一性相矛盾.

定理1KQn是一个分次Frobenius代数当且仅当Q形如图1.

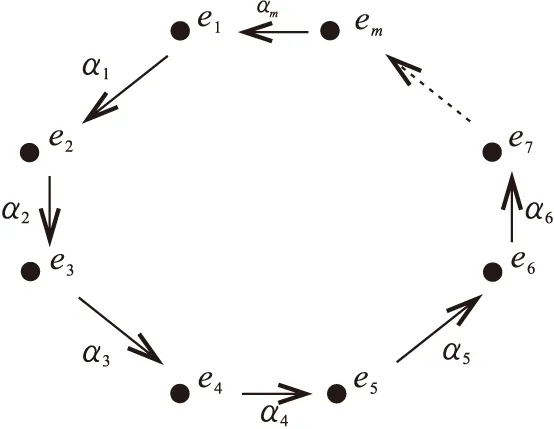
图1 箭图QFig.1 Quiver Q

证明必要性 由命题2已显然,证明充分性只需给出分次Frobenius形式的映射σ,具体定义如下：

σ(0,x)=σ(x,0)=0,∀x∈KQn,

σ(k1p,k2q)=k1k2δn,k+lδs(αi1),t(αj1),∀p=αik…αi1≠0,q=αjl…αj1≠0,k1,k2∈K.

易验证上述的σ是分次Frobenius的.

命题3如果KQn是一个分次对称代数,那么命题1中所述的路为圈.

证明由对称性

σ(ei,αinαin-1…αi1)=σ(αinαin-1…αi1,ei)≠0,

可得

t(αinαin-1…αi1)=s(αinαin-1…αi1)=ei.

证毕.

证得命题3,结合定理1可直接得到定理2.

定理2KQn是一个分次对称代数当且仅当Q形如图1，其中m|n.

定理3

KQn=KQ/〈∂pw;|p|=n〉,

其中

〈∂pw;|p|=n〉={w|∂pw≠0,|p|=n}.

Frobenius代数KQn的Nakayama自同构可由

μ(e1)=en(≡m)+1,μ(α1)=αn(≡m)+1

确定.

证明对于箭图Q中的路p=αl…α2α1,∂p有具体作用

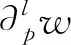
先考虑集合,有

再考虑元素,有

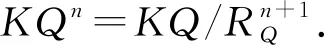
对于Frobenius结构映射σ(箭图形如定理1),有

σ(αnαn-1…α2α1,e1)=σ(μ(e1),αnαn-1…α2α1),

σ(αnαn-1…α2,α1)=σ(μ(α1),αnαn-1…α2),

其中αn=αn(≡m)+1.至此可知

μ(e1)=en(≡m)+1,μ(α1)=αn(≡m)+1.

3 通过扭超势构造(由箭图诱导的)分次Frobenius代数

设由箭图诱导的结合代数A=A0⊕A1⊕A2⊕…⊕Al是一个长度为l的分次Frobenius 代数,伴有Frobenius结构映射σ和Nakayama自同构μ,其中

A0=R=KQ0,A1=V=KQ1,|Q0|=m,|Q1|=n.

定理4记

如果由箭图诱导的结合代数A=A0⊕A1⊕A2⊕…⊕Al是一个长度为l的分次Frobenius代数,那么存在余代数同构A*≅〈ξ〉.

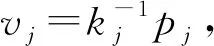
其中

并且满足

v*(pj)=σ(αjl,αjl-1…αj2αj1).

因为

v*(pj)=v*(αjlαjl-1…αj2αj1)=v*((π(αjl))(π(αjl-1…αj2αjl))=ΔA*(v*)(π(αjl)⊗π(αjl-1…αj2αj1))=

(π*⊗π*)∘ΔA*(v*)((αjl)⊗(αjl-1…αj2αj1))=ΔT(V*)∘π*(v*)((αjl)⊗(αjl-1…αj2αj1))=

所以

σ(αjl,αjl-1…αj2αj1)=hj1j2…jl-1jl.

即

取ξ=π*(v*),有〈ξ〉⊆π*(A*),下证反包含关系.

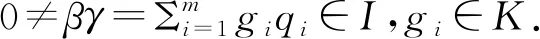
dim(Il)≥1.

dim(Bl)≥m.

综合引理1和引理2有推论

dim(Al)=dim(A0)=m.

它们的维数关系显然与A/I≅〈ξ〉*矛盾,即证得I=0.

命题4定理4所记的ξ为余代数自同构下的扭超势.

证明设

则有

从而

证得

命题5如果C=〈ϖ〉是由长度为l的扭超势ϖ生成的T(V*)的分次子余代数,那么

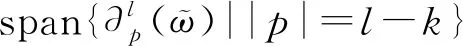
证明定义一个平移变换如下：

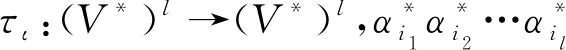
由扭超势的定义可知在箭图自同构ι下：

ϖ=τι(ϖ).

此时

注意到

|p|=|ι(p)|=l-k,

可得

可表

即知

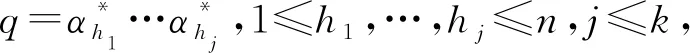
即

同理可知

证得

定理5如果ϖ∈T(V*)是一个扭超势,那么A=〈ϖ〉*是一个长度为|ϖ|的分次Frobenius代数.

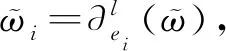
定义映射σ:A×A→K如下：

不难验证它是一个双线性映射：

∀x,y,z,x1,x2,y1,y2∈A,k∈K,

(1)σ(xy,z)=σ(x,yz)；(2)σ(x1+x2,y)=σ(x1,y)+σ(x2,y)；

(3)σ(x,y1+y2)=σ(x,y1)+σ(x,y2)；(4)σ(kx,y)=σ(x,ky)=kσ(x,y).

下面证明它是非退化的,即:

∀γ∈Ai,∃θ∈A|ϖ|-i,σ(γ,θ)≠0.

设βii1,…,βiij是Ai的一组基,表γ=kii1βii1+…+kiijβiij.再由命题5可表

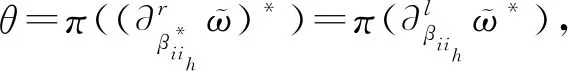
非退化性得证.

对于任意的1≤i≤|ϖ|,i1≤ih≤ij,由γ的任意性有

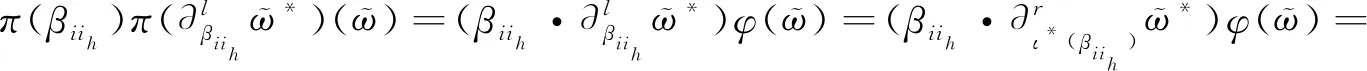
亦即

证得ι*就是分次Frobenius代数A的Nakayama自同构.

4 一些例子

示例1取图1中m=4,即箭图Q′形如图2.

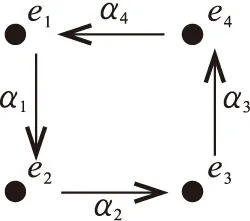
图2 箭图Q′Fig.2 Quivers Q′

则I=〈α3α2α1,α4α3α2,α1α4α3,α2α1α4〉诱导了一个长度为2的分次Frobenius代数.

说明I诱导了一个路代数KQ的商代数A=A0⊕A1⊕A2,其中

A0=KQ0,A1=KQ1,A2=KQ2.

分次代数A的Frobenius结构映射σ的非退化性表现在

σ(α2,α1)=σ(α3,α2)=σ(α4,α3)=σ(α1,α4)≠0,

并且满足

σ(x,y)=0, ∀x∈Ai,y∈Aj,i+j≠2.

其Nakayama自同构μ如下：

μ(e1)=e3,μ(e2)=e4,μ(e3)=e1,μ(e4)=e2;

μ(α1)=α3,μ(α2)=α4,μ(α3)=α1,μ(α4)=α2.

示例2取箭图Q逆箭向的对偶箭图,即箭图Q*形如图3.

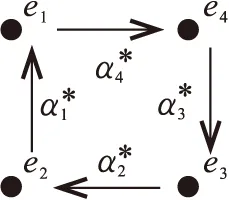
图3 箭图Q*Fig.3 Quivers Q*

设

这是一个箭图自同构ι=id下的扭超势,则A=〈ϖ〉*是一个长度为4的分次Frobenius代数.

说明记C=〈ϖ〉,这是一个长度为4的扭超势ϖ生成的T(V*)的分次子余代数,其中

可利用余乘得到其分次结构如下：

C0=span{e1,e2,e3,e4}.

从而A=A0⊕A1⊕A2⊕A3⊕A4,其中

A0=KQ0,A1=KQ1,A2=KQ2,A3=KQ3,A4=KQ4.

即有限维结合代数A是图2中m=n=4时的分次对称代数.

同示例1,可由长度为4的分次Frobenius代数A的结构映射σ知

σ(α4α3α2,α1)=σ(α1α4α3,α2)=σ(α2α1α4,α3)=σ(α3α2α1,α4)=k≠0.

此时