浅谈二次函数中动点探究

梁和

◆摘  要：动点问题一直是初中阶段的热点问题，近几年来的中考过程中，对学生的动点问题考察层出不穷。在中学阶段二次函数的动点问题一直被学生成为“顽固分子”这就需要配教师在教学的过程中，结合实际的例题来为学生进行分析，从而总结出二次函数动点问题的解题思路，帮助学生更好的解决二次函数动点问题。

◆关键词：二次函数;动点问题;数学教学

在初中的数学过程中，将数学知识分为了来能够大部分，分别为几何与函数。但是二次函数动点问题的出现，将这两方面的数学知识进行了整合，使得学生在进行二次函数的动点问题解决时，能够融入相应的几何知识。因此这种综合式的考察方法，能够帮助学生更好的将数学作为一整个完整的体系来进行学习。以下是几种常见的二次函数动点问题。

一、二次函数动点构建直角三角形

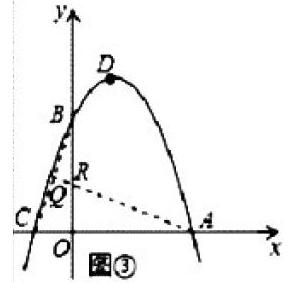
一直二次函数y=ax2+bx+3的图象分别与x轴交于点A（3，0），C（-1，0）与y轴交于点B，点D为二次函数图象的顶点，首先求出二次函数的关系式，其次求出在X轴上取动点P（m，0）且1

本题一共分为了三个部分，第一部分是求出二次函数的关系式，在解题的过程中，只需要将A点的坐标以及C点的坐标带入原题当中已经给出的函数方程式这样就能够得出二次函数的关系式为y=-x2+2x+3。

在第二部分的解题过程中，我们已知动点的取值范围以及在第一部分解出的方程式，并且知道点。因此我们可以通过带入，找到点D的具体坐标：y=-x2+2x+3=-（x-1）2+4这样得出点D的坐标为（1，4）。然后设线段A表所在的直线的函数关系式为y=kx+c然后分别将A点的坐标（3，0）以及C点的坐标（-1，0）进行带入，得出函数关系式：y=-x+3同理可知线段AD所在的直线关系是为y=-2x+6。原题中给出了点p的坐标为（m，0）点E的坐标就是（m，-m+3）点F的坐标就是（m，-2m+6）因此得出EP之间的距离为-m+3，EF之间的距离为-m+3从而得知EF=EP。

在第三部分的解答过程中，就可以通过构建直角三角形来解决。

我们可以链接BC，过点R做RQ⊥BC，垂足为Q。这样在二次函数当中就出现了两个直角三角形，一个是RT△CQA，一个是RT△BCO。我们知道C的坐标为（-1，0）这样就能够得到OC=1，OB=3根据勾股定理可以得知，BC为的距离，并且通过两个直角三角形得知△BQR与△AOB为相似三角形，进一步求得RQ与BR之间的关系，从而得知当A，R，Q三点共线时，值最小、这样救恩能够通过相似三角形的定理来解出最小值。

二、二次函数动点构建特殊四边形

在二次函数的动点问题解决过程中，学生还会遇到与四边形相关的内容，这时学生就需要根据自己的所学内容，来构建一个特殊的四边形。

如图，已知抛物线C1与坐标轴的交点是A（-4，0）B（-2，0）E（0，8）求抛物线C1关于原点对称的抛物线C2的解析式;设抛物线C1的顶点为M，抛物线C2与x轴分别交于C、D两点，顶点为N，四边形MDVA的面积为S.若点A，点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动，与此同时，点M，点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动，直到点A与点D重合为止。求出四边形MDN4的面积S与运动时间1之间的关系式，并写出自变量1的取值范围;当1为何值时，四边形MDN4的面积S有最大值。

在这一题当中总共分为了四个部分。在第一部分解答过程中，可以先确定点A，B，E关于原点的对称点点D，C，F通过这六个点，带入抛物线C2的解析式从而得出抛物线的解析式：y=-x2+6x-8。

在第二部分的解题过程中，由（1）的结果可以算出点M和N的坐标：M（-3，-1）N（3，1）然后添加辅助线过点N作NH⊥AD，垂足为H当运动到时刻t使，AD=2OD=8-2t，NH=1+2t。根据中心对称的性质，可知MDNA组成了一个平行四边形。这样就能够通过平行四边形的面积来计算出点t的取值范围。

在第三部分的解答过程中直接将t的取值范围带入到计算公式当中即可。在第四部分的解答过程中，主要考察动点以及举行的定义。因此可以通过AD=AM来证明四边形MDNA为矩形，从而解出t的值。

三、二次函數动点构建等角三角形

如图，已知抛物线y=-=x2+hx+c与坐标轴交于ABC三点，点A的横坐标为-1，过点C（0.3）的直线y=-3/4tx+3与x轴交于点Q，点P是线段BC上的一个动点PH⊥OB于点H.若PB=5t，且0<1<1.确定b，c的值;写出点B.Q.P的坐标（其中Q.P用含t的式子表示）;依点P的变化，是否存在t的值，使△PQB为等腰三角形？

这一题考查了函数、相似性代数、几何知识等问题，尤其是在第三部分，主要是对于等腰三角形的分类讨论。这一类的二次函数动点问题相对解法较多，学生在解决问题的过程中可以尝试着用多种方式进行解答。

第一部分通过带入可知b=9/4，c=3，第二部分为B（4，0）Q（4t，0）P（4-4t，3t）第三部分t的值会有三种不同的情况：

第一种情况是PQ=PB，这时PH与OB垂直，GH=HB所以t的值为1/3

第二种是PB=QB这时t的值为4/9

第三种使PQ=BQ，在这种情况下，我们可以用三种方式进行解答：

第一种，可以过点Q做辅助线QD⊥BP，通过PQ=QB可以得出BD的距离，然后根据相似三角形的定理，可以得出t的值。

第二种，做RT△OBC的斜边中线OE这样的值OE与BE相等，从而△OEB与△PQB为相似三角形，同样也能得知t的值。

第三种，在RT△PHQ中有OH2+PH2=PQ2所以可以求出t的值

近几年的中考数学试卷当中，二次函数的动点问题一直以压轴题的形式出现，同时也是将几何与函数进行融合的一种题型，因此教师可以将此作为一个独立模块对学生进行针对性的教学，从而促进学生数学知识点掌握。

参考文献

[1]二次函数图像动点与相似三角形融合的中考题解决策略探究[J].中学数学，2020（06）：72-73+85.

[2]郑博文.初中数学二次函数动点问题的教学策略研究[J].课程教育研究，2019（45）：131.