合同变换及其应用

李玲丹，白丽艳

(玉溪师范学院 数学与信息技术学院 数学系，云南 玉溪 653100)

德国数学家克莱因的论文《关于近代几何研究的比较考察》根据变换群理论的观点，给出了清晰的几何新定义，几何被定义为研究图形在某个变换群下的不变性质的学科[1]．中学涉及的几何课程中，无论是课程内容还是教师教学，都引入了几何变换的思想，在这样的形势下，如何有效且高效地运用几何变换的观点和思想方法来解决中学学习中涉及到的相关问题，已成为当今数学课程改革中的一种新思维方式．

在初等几何相关的解题过程中，作辅助线往往是解决初等几何问题的要点所在．而由于几何问题的多变，不同题型所作辅助线的方法也是不同的．在这种情况下，就可利用初等几何变换来进行有效分析，运用多种变换对题中给出的各个条件进行集中处理，通过观察变换后的各个条件之间的关系，即可得到较为清晰的证题思路．而合同变换作为初等几何变换中的一大类，对于解决初等几何问题意义重大．基于此，本文探索研究了在初等几何问题中正确应用合同变换的方法．

定义[2]一个平面到其自身的变换W，如果对于该平面上的任意两点A、B和它们的像点A′、B′之间，恒有距离A′B′=AB，那么这个变换W就叫做平面上的合同变换．

合同变换的基本形式有平移、旋转、轴反射变换3种．下面，将对合同变换所包括的平移变换、旋转变换、轴反射变换在各类型初等几何问题中的应用进行论述.

1 平移变换

1.1 平行四边形与平移变换

若平面几何的题设条件中含有平行四边形，则可想到用平移变换来对问题进行处理，对于平移向量的起点和终点的选择，可根据所要解决的问题来选择平行四边形的某两个相邻顶点．

例1[3]设Q是平行四边形ABCD内部一点．

求证：∠BAQ=∠QCB当且仅当∠QBA=∠ADQ．

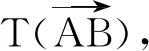
设Q的对应点为Q′，则∠BCQ′=∠ADQ，且四边形ABQ′Q是一个平行四边形．

∴∠BAQ=∠QQ′B，∠QBA=∠BQQ′，

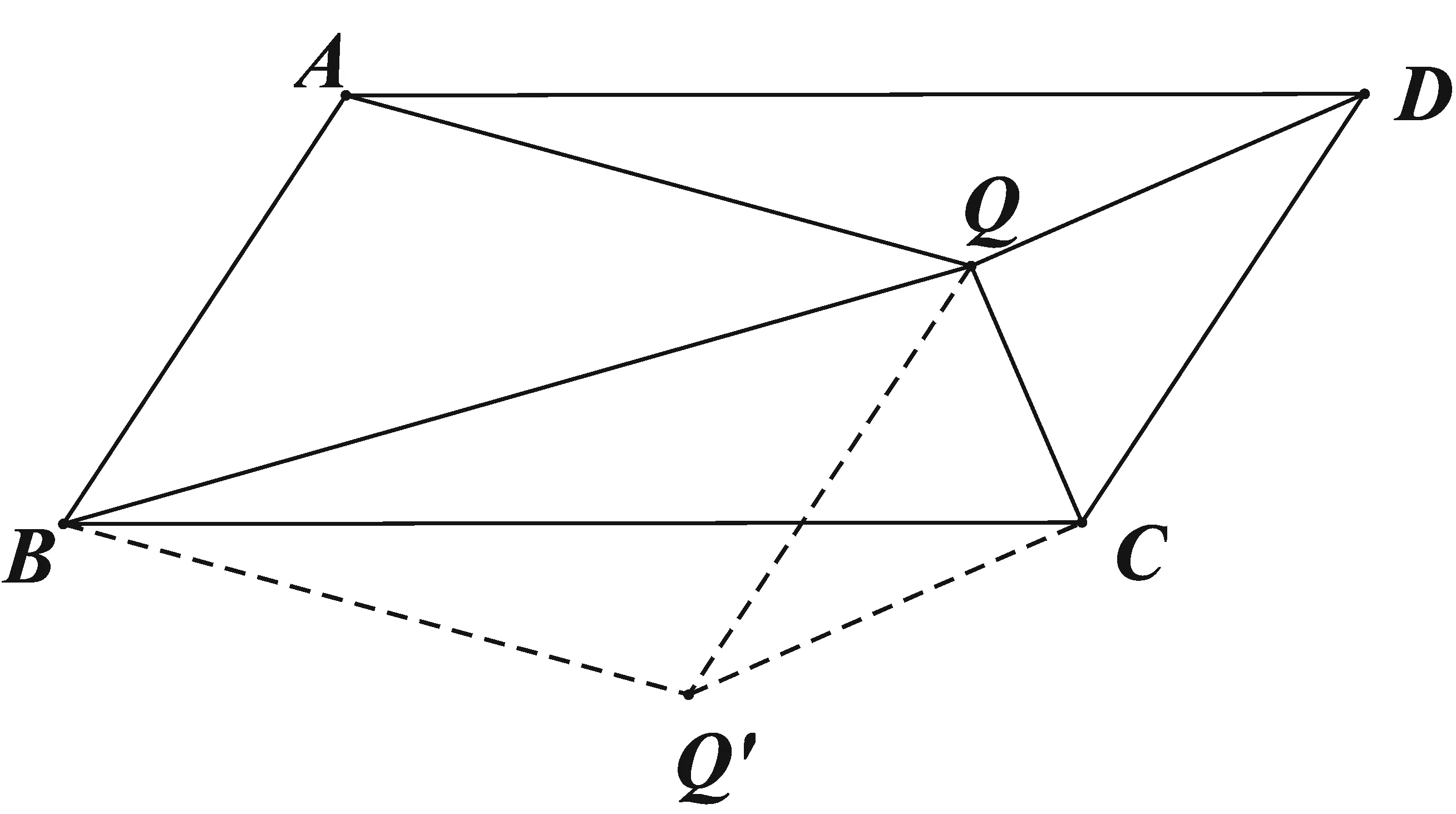
图1

则∠BAQ=∠QCB，

⟺∠QQ′B=∠QCB，

⟺B、Q′、C、Q四点共圆，

⟺∠BQQ′=∠BCQ′，

⟺∠QBA=∠BCQ′，

⟺∠QBA=∠ADQ，

1.2 共线相等线段与平移变换

在平面几何问题中，若该问题的条件中给出两条相等的线段，并且这两条线段在同一条直线上，那么我们就可以考虑利用平移变换来对问题具体分析．一般来说，所选的平移向量需使其中一条线段通过平移变换与另一条线段重合．

例2 设点M、N是△ABC边BC上两个点，BM=NC．∠BAM=∠NAC

求证：△ABC为等腰三角形.

则B的对应点为N，M的对应点为C,设A的对应点为A′，则AA′∥BC，

∴四边形ANCA′是一个梯形，

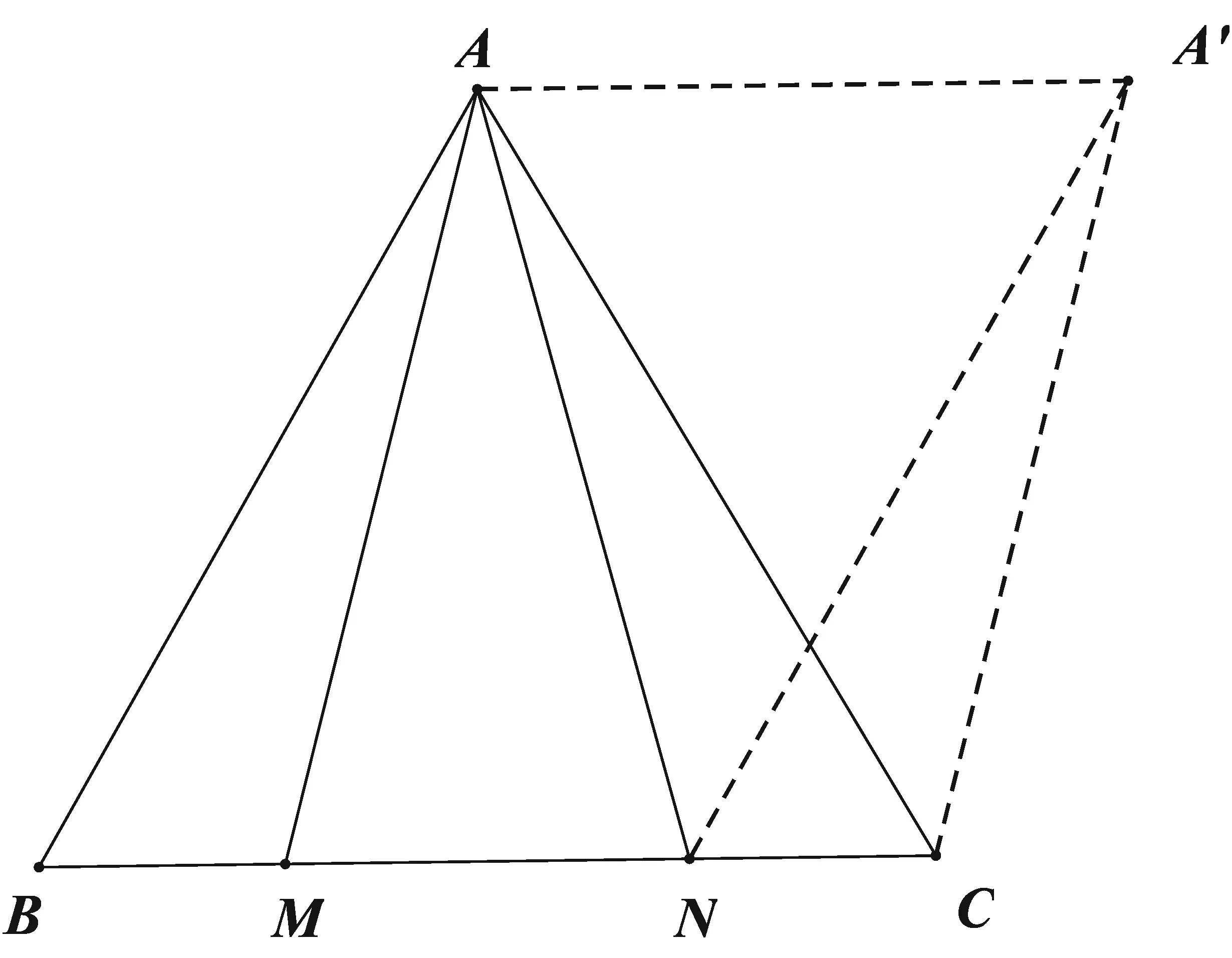
图2

又A′N=AB，A′C=AM

已知BM=NC，

∴△A′NC≌△ABM，

∴∠NA′C=∠BAM=∠NAC，

∴四边形ANCA′是一个圆内接梯形，

由此四边形ANCA′为等腰梯形，

∴AC=A′N=AB，

故△ABC是等腰三角形．

1.3 一般相等线段与平移变换

如果给出的两条长度相等的线段没有特殊关系，那么对于这两条线段，可以利用平移变换来处理:对其中的一条线段进行平行移动，使得这两条线段的某个端点经过平移变换后重合，由于两线段的长度相等，则变换后的图形可与等腰三角形相关，那么就可利用等腰三角形有关性质来对问题进一步分析．

例3[3]设E、F分别是ABC的边BC、AC上的点，且BE=AF，AE与BF交于点G，∠ABC的角平分线CD与AE、BF、AB分别交于点H、I、D．

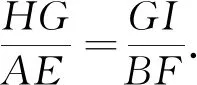
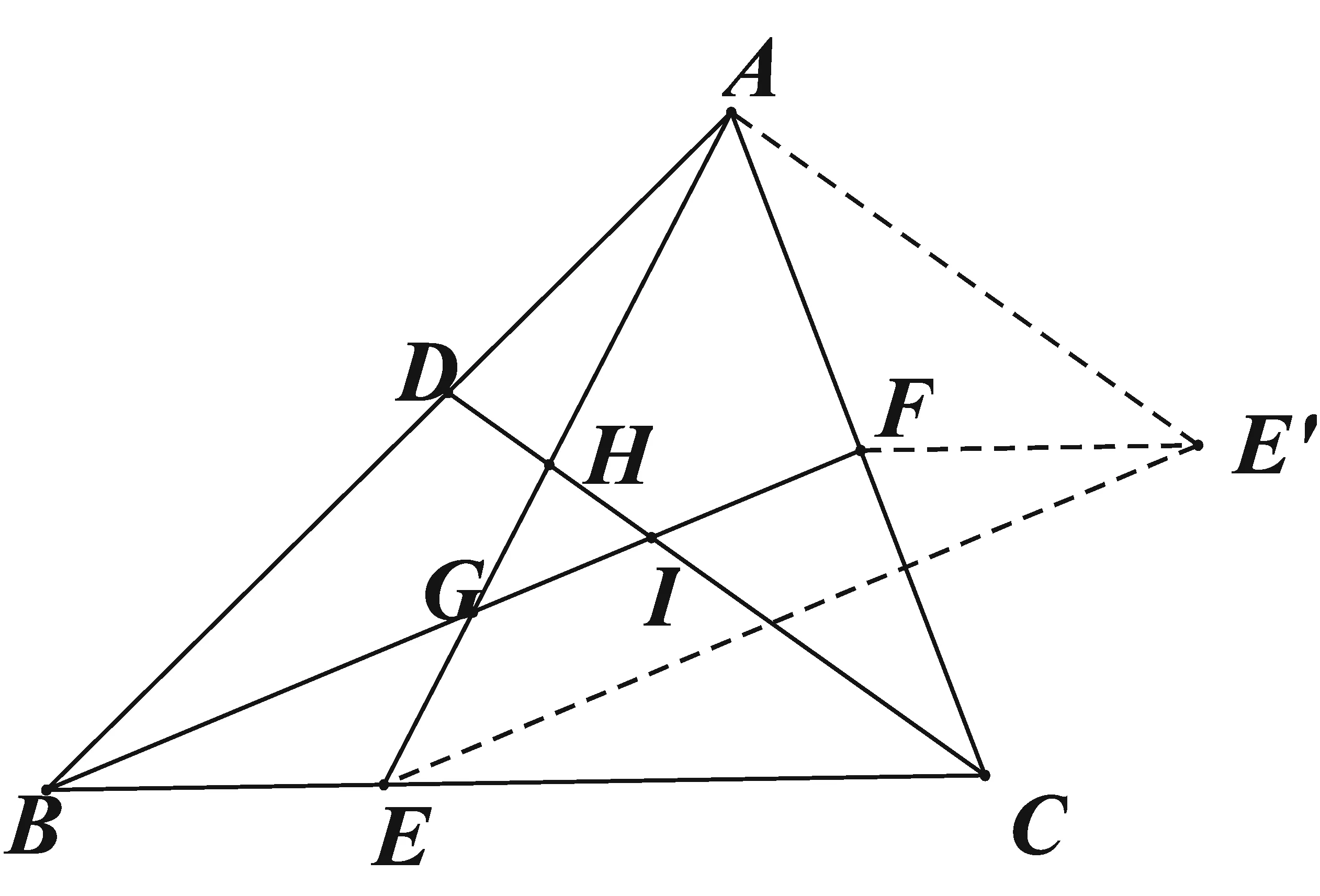
图3

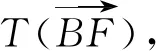
则BFEE′，BEFE′，

∵AF=BE，

∴AF=FE′，∠CAE′=∠AE′F，

又FE′BC，

∴∠E′FC=∠FCB，

∴∠E′AG=∠ACD，则AE′∥DC，

∴∠GHI=∠EAE′，

又∵BF∥EE′，∴∠HGI=∠AEE′，

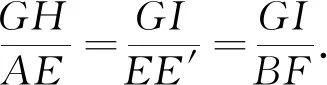
1.4 平行与平移变换

在同一平面内，通过平移得到的两条直线是互相平行的．因此，若是已知条件中含有与平行相关的平面几何问题，同样可以用平移变换来进行探究，平移方向及距离根据问题确定．

例4[3]设AM是△ABC的角平分线，任做一条直线l分别与BC、CA、AB交于点P、Q、R．

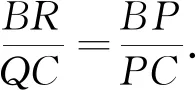
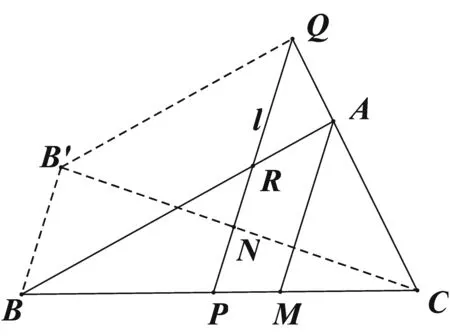
图4

∴B′Q=BR，∠BAC=∠B′QC，

设B′C与l交于点N，则NP∥B′B，

又AM平分∠BAC，于是由三角形的角平分线定理与判定定理,得

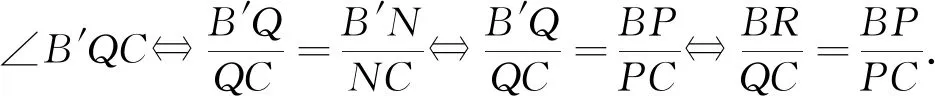
2 旋转变换

设O是平面π上一个定点，θ是一个定角(有向角)，如果平面π的一个变换，使得对于平面π上任意一点A与其像点A′之间，恒有：

(1)OA′=OA；

(2)有向角∠AOA=θ．

则这个变换称为平面π的一个旋转变换，记作R(0,θ)，其中定点O称为旋转中心，定角θ称为旋转角或转幅[3]．当θ=180°时的旋转称为半周旋转，又叫作中心反射或中心对称变换，记作C(O)[3].

2.1 中点与中心反射变换

已知线段的中点即为这条线段的反射中心，由此，若题干给出某线段中点，则可用中心反射变换处理，反射中心即为此线段中点.

例5 过直角△ABC的斜边BC的中点P与直角顶点A作一个圆分别与两直角边AB、AC交于点M、N．

求证：BM2+CN2=MN2.

证明：如图5所示，做中心反射变换C(P)，则C的对应点为B．设N的对应点为N′，则P为NN′的中点，NB′CN．

∵BA⊥CA，

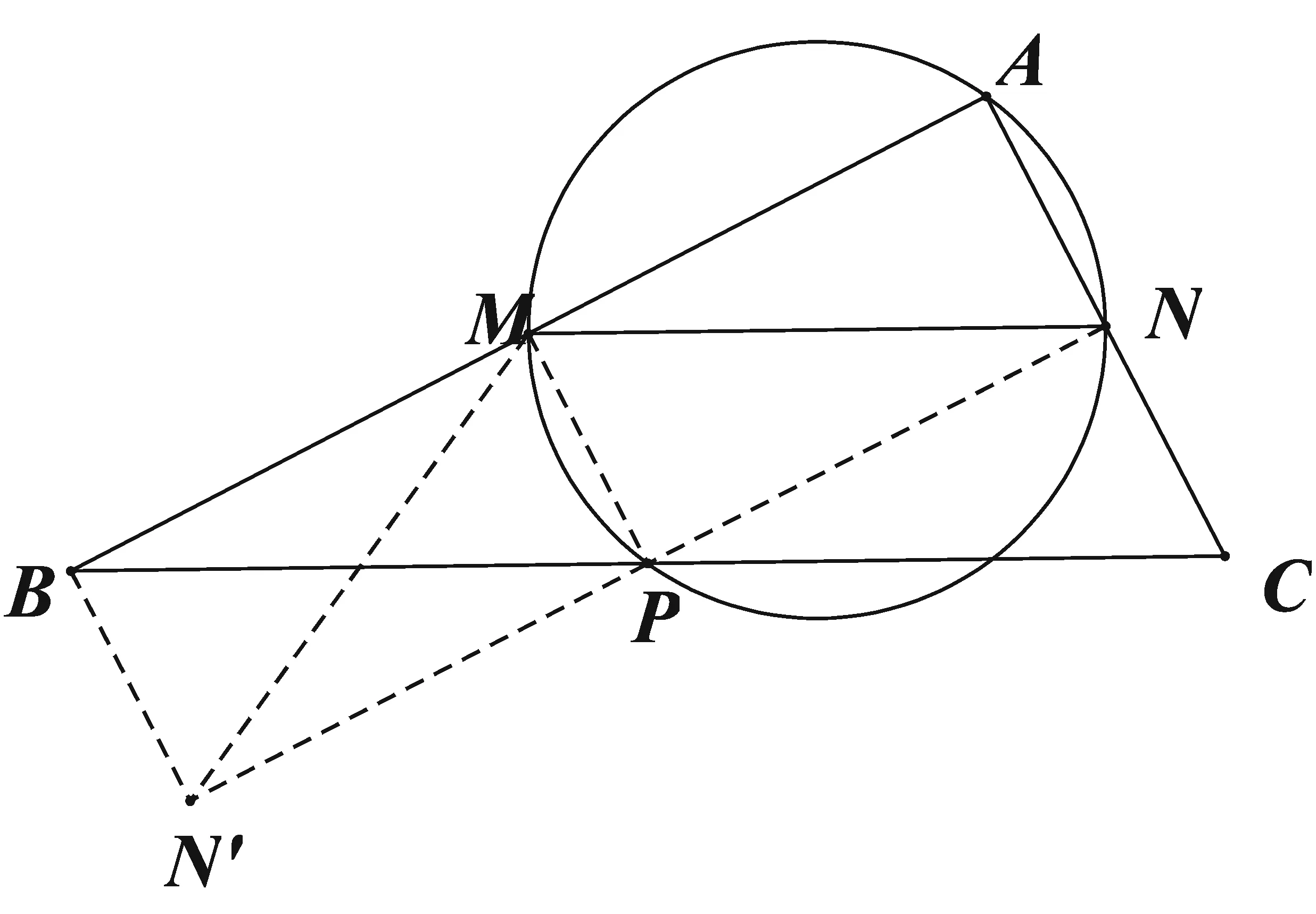
图5

∴BM⊥CN，

∴BM⊥BN′.

∵∠BAC为直角，

∴MN为圆的直径，

∴MP⊥PN，

则MP⊥NN′.

又P为NN′的中点，

∴MN′=MN.

由△MBN′是直角三角形，BM2+CN2=BM2+BN′2=MN′2=MN2.

2.2 平行四边形与中心反射变换

平行四边形是中心对称图形．所以，若一个平面几何问题中含有与平行四边形相关的条件，可以根据题设条件选择利用中心反射变换进行处理，此时，该变换的反射中心就是平行四边形的中心．

例6[3]设Q为平行四边形ABCD的AD边中点，过点C作AB的垂线交AB于点P．

求证：∠PDQ=3∠QPA的充分必要条件是BC=2AB．

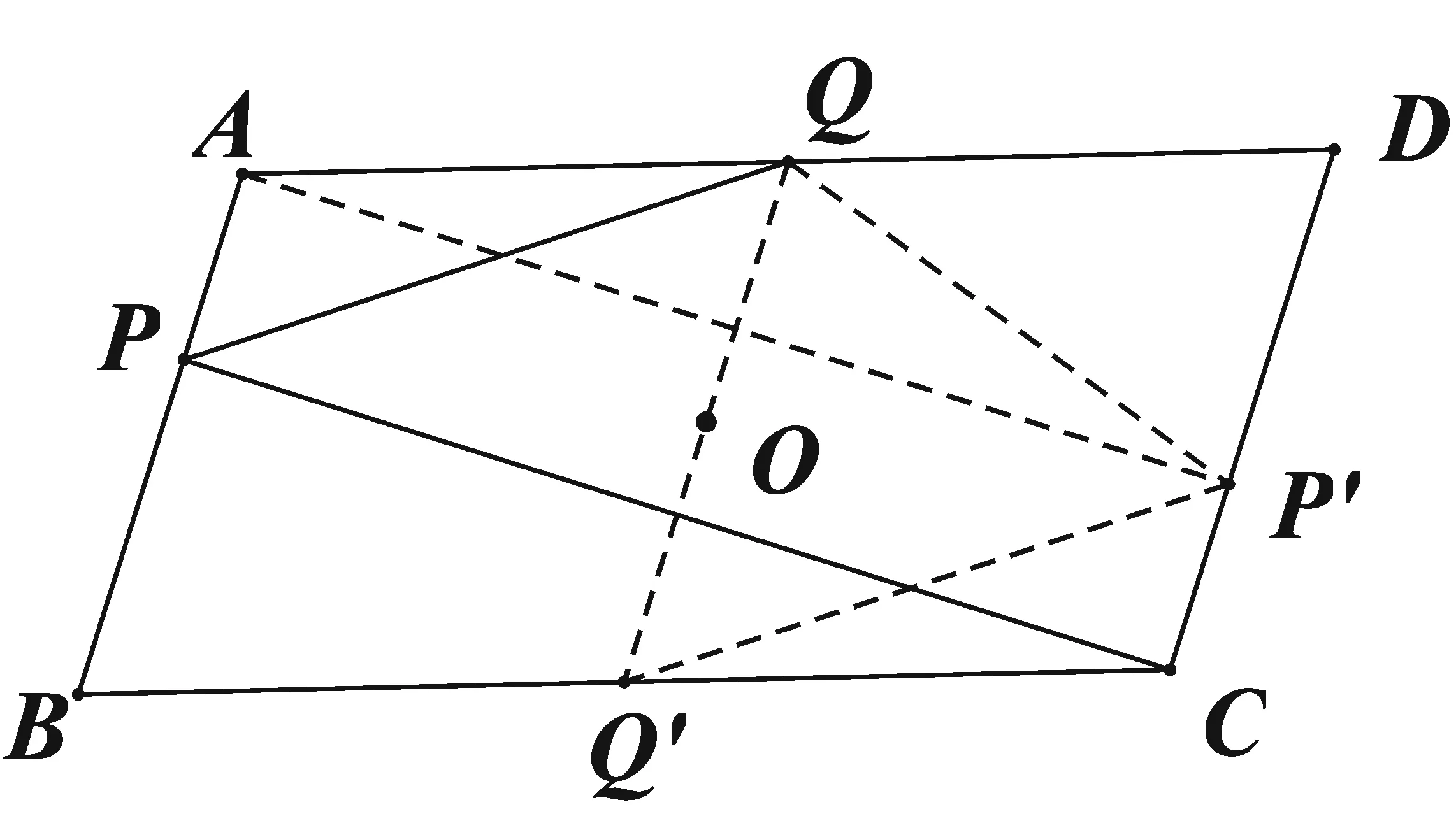
图6

证明：如图6所示，以平行四边形ABCD的中心O点为反射中心作中心反射变换C(O)，则A的对应点为C，B的对应点为D，D的对应点为B．设P的对应点为P′，Q的对应点为Q′，则P′在直线CD上，Q′为BC的中点,且AP′⊥CD，QQ′ABCD，∠Q′P′C=∠QPA=∠PQQ′,∠QQ′D=∠P′CQ′．

又Q为Rt△AP′D的斜边AD的中点，

∴QP′=QD=Q′C，

∴四边形P′QQ′C是以QQ′、P′C为两底的等腰梯形，

∴∠Q′QD=∠P′CQ′=∠QP′C，

则∠PQD=3∠QPA⟺∠PQQ′+∠Q′QD=3∠QPA⟺∠QPA+∠Q′QD=3∠QPA

⟺∠Q′QD=2∠QPA⟺∠QP′C=2∠Q′P′C⟺∠QP′Q′=∠Q′P′C

⟺AB=AQ⟺AD=2AB⟺BC=2AB.

2.3 正三角形与旋转变换

正三角的三边相等且三个角均为60°，若一个平面几何问题给出的条件中有与正三角形相关的内容，可根据已知条件进行旋转变换，该变换的旋转角即为60°，旋转中心则根据所需解决的问题来选择正三角形的顶点．

例7[4]设M为等边△ABC内的一点，且MA=a，MB=b，MC=c，求△ABC的面积．

解：如图7所示，将△MAB、△MBC、△MCA分别绕着点A、B、C按逆时针方向旋转60°，使AB、BC、CA分别与AC、BA、CB重合，这时△MAB、△MBC、△MCA分别旋转到△PAC、△QBA、△RCB所在的位置．

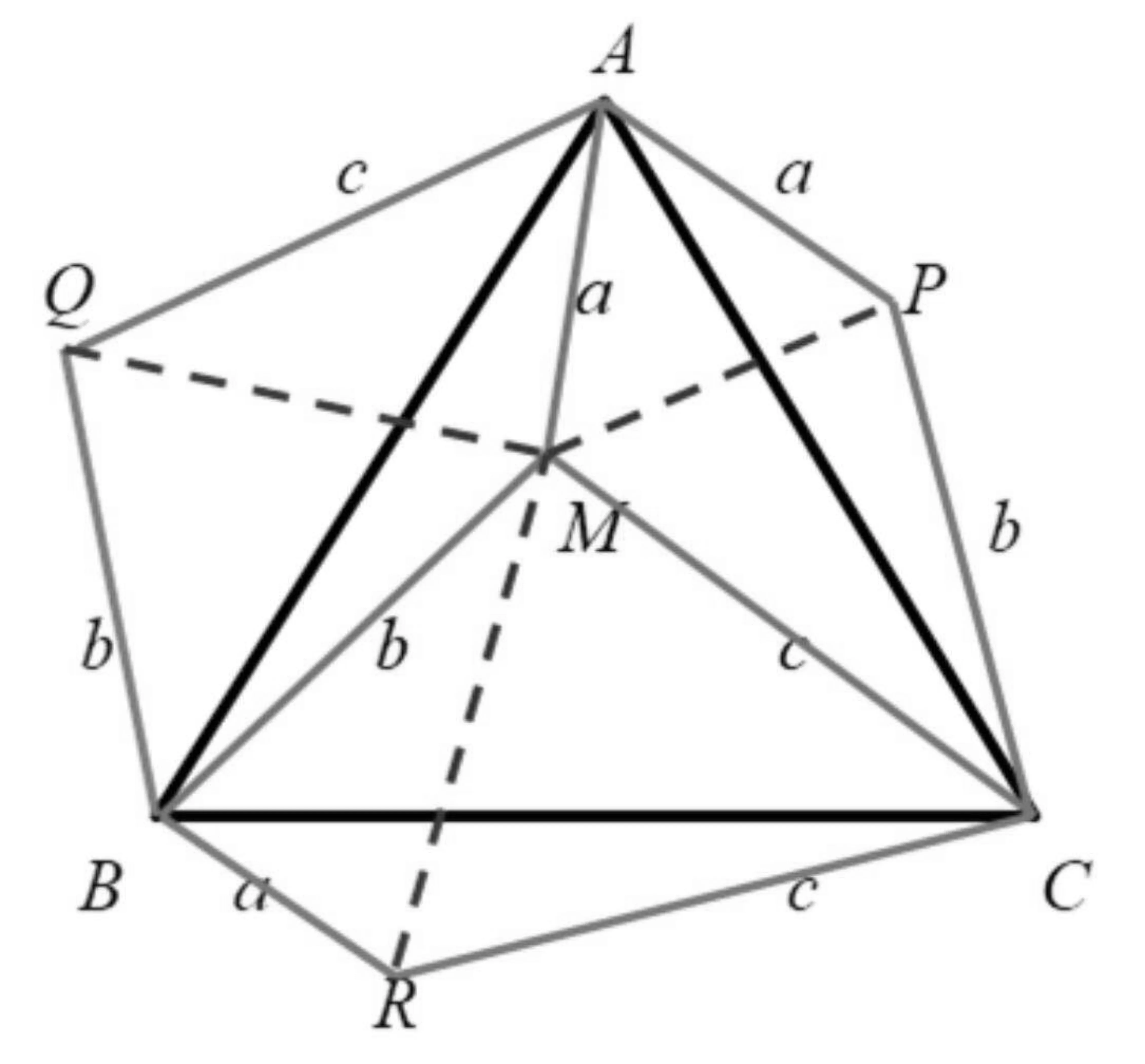
图7

由△MAB≌△PAC，△MBC≌△QBA，△MCA≌△RCB，

得MA=PA=RB=a，MB=QB=PC=b．MC=RC=QA=c

∠BAC=∠NAP=60°，∠ABC=∠MBQ=60°，∠BAC=∠MCR=60°，

由MA=PA=a，∠MAP=60°，得△MAP为正三角形．

同理，△MBQ和△MCR为正三角形，

∴MP=a，MQ=b，MR=c，即△MAQ≌△MBR≌△MCP，则

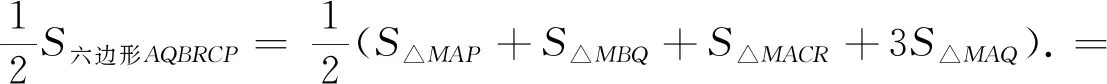
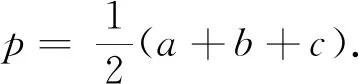
2.4 正方形与旋转变换

由于正方形的特殊性质，在一个平面几何问题中，如果题设给出的条件中含有与正方形相关的内容，那么就可以考虑用旋转变换来处理，旋转角为90°．旋转中心选为正方形的一个顶点．

例8[3]设M、N分别为正方形ABCD的边DC、AD上的点.

求证：BM=CM+AN的充分必要条件是BN平分∠ABM．

证明：如图8所示，作旋转变换R(B,90°)，则C的对应点为A.设M的对应点为M′，则BM′=BM，AM′=CM，且∠ABM′=∠CBM，M′在DA的延长线上，

∴NM′=AM′+AN=CM+AN，

又∠M′NB=∠CBN，

∴BM=CM+AN，

图8

⟺BM=NM′，

⟺BM′=NM′，

⟺∠BNM′=∠NBM′，

⟺∠CBN=∠NBM′，

⟺BN平分∠CBM′，

⟺BN平分∠MBA.

3 轴反射变换

设l是平面π上的一条定直线，若通过平面π上的一个变换，可以使平面上不在直线l上的任意一点A与其经过变换得到的对应点A′之间的连线AA′恒被直线l垂直且平分，而直线l上的点是保持不动的，那么，这个变换就称为平面π的轴反射变换，其中，定直线l就是这个轴反射变换的反射轴[3]．

3.1 等腰三角形与轴反射变换

等腰三角形是轴对称图形，因此，当题设条件中有涉及等腰三角形相关的条件时，可以考虑利用轴反射变换来对问题进行处理，此时，该变换的反射轴就是等腰三角形的对称轴所在的直线．

例9 在等腰△ABC中，AB=AC，D是△ABC的内一点．

求证：∠ADB>∠CDA的充分必要条件是DC>DB．

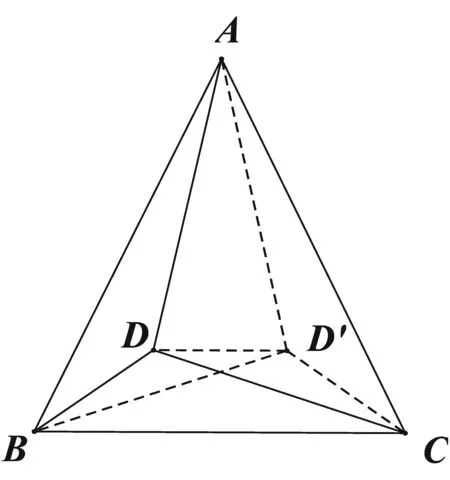
图9

证明：如图9所示，对等腰△ABC作轴反射变换，反射轴为等腰△ABC的对称轴．则B的对应点为C，C的对应点为B,设D的对应点为D′，则D′依然位于△ABC的内部.且DD′∥BC，△AD′B=△ADC，△DCB=△D′BC，则

△ADB>△CDA

⟺△ADB>△AD′B

⟺点D在△ABD′内部

⟺△DBC>△D′BC

⟺△DBC>△DCB

⟺DC>DB．

3.2 角平分线与轴反射变换

角是轴对称图形，当一个平面几何问题中给出了某个角及其角平分线时，可以考虑利用这个角及其角平分线来作轴反射变换，反射轴即角平分线所在直线.

例10[2]已知DH为直角△ABC斜边上的高，AF平分∠BAC交BH于点E，

EP∥AC，交CB于点P.

求证：BE=CP.

证明：如图10所示，以∠BAC的角平分线为对称轴作轴反射变换,则B的对应点为B′，B′必在AC边上,且AB=AB′，EB=EB′，∠ABE=∠AB′E.

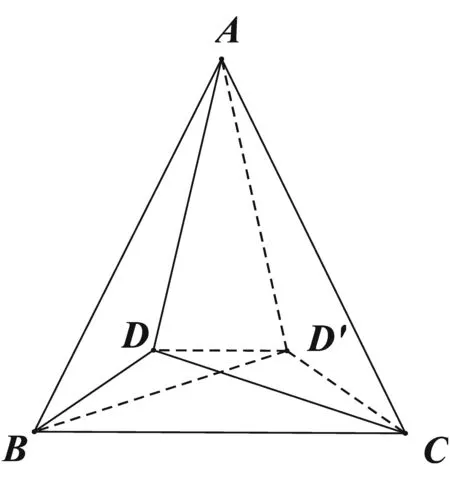
图10

∵△ABC是直角三角形，且BH⊥AC，

∴∠ABH=90°-∠HBC=∠C，

∵∠ABH=∠AB′E，

∴∠AB′E=∠C，故EB′∥PC，

又已知EP∥AC，

∴四边形EPCB′是平行四边形，

∴B′E=CP，

又∵BE=B′E，

∴BE=CP．

3.3 垂直与轴反射变换

以直角的其中一边为反射轴来作轴反射变换，则变换前后的图形刚好为一个平角，因而，若平面几何问题中给出有关垂直条件，那么此时就可以利用轴反射变换来解决问题．

例11[3]设AD是△ABC的一条高，H是直线AD上的一点.

求证：点H是△ABC的垂心．

证明：如图11所示，以BC边为对称轴作轴反射变换，设H的对应点为H′，则H′在直线AD上，且∠CH′B=∠BHC=180°-∠BAC，即∠CH′B+∠BAC=180°，则A、B、H′、C四点共圆，

∴∠H′AC=∠H′BC，

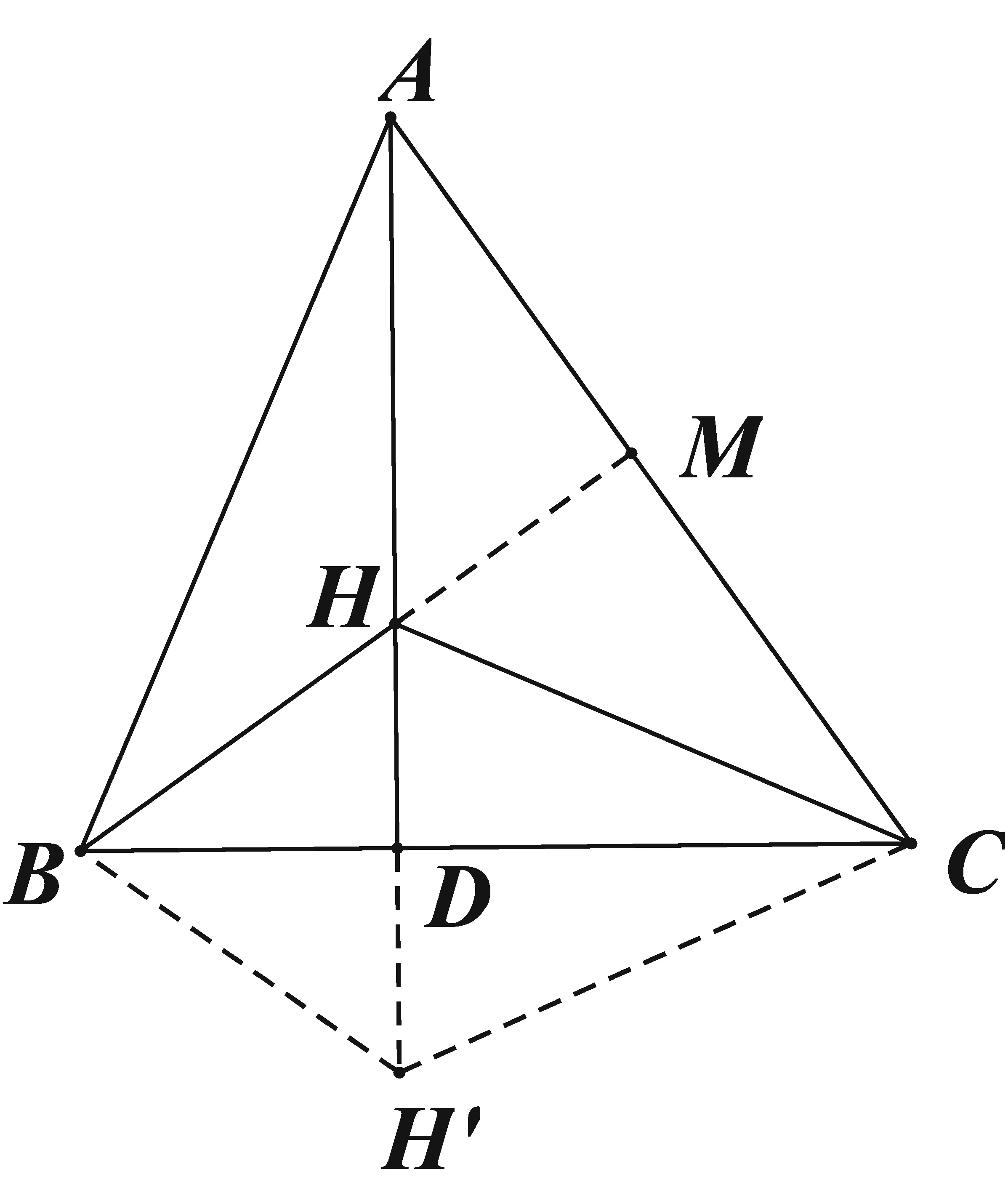
图11

∴∠H′AC=∠CBH，

即∠DAC=∠CBH，

设直线BH与AC交于点M，

则∠DAM=∠DBM，

∴M、A、B、D四点共圆，

∴∠AMB=∠ADB=90°，

∴BH⊥CA，

故点H是△ABC的垂心．

3.4 30°的角与轴反射变换

以30°角的其中一边为对称轴作轴反射变换，则变换前后的图形可构成一个60°的角，故在一个平面几何问题中，若题设给出的条件中含有30°角，则可对其做轴反射变换，反射轴为角的其中一边.

例12[3]在△ABC中，∠BAC=30°，∠CBA=50°，G是△ABC内一点，∠BAG=20°，∠ACG=40°．求∠GBA．

解：如图12所示，以AC边为对称轴作轴反射变换，设B的对应点为B′，则∠BAB′=60°，AB′=AB，即△ABB′为等边三角形，

∠AB′C=∠CBA=50°，∠CAB′=∠CAB=30°，又∠BAG=20°，

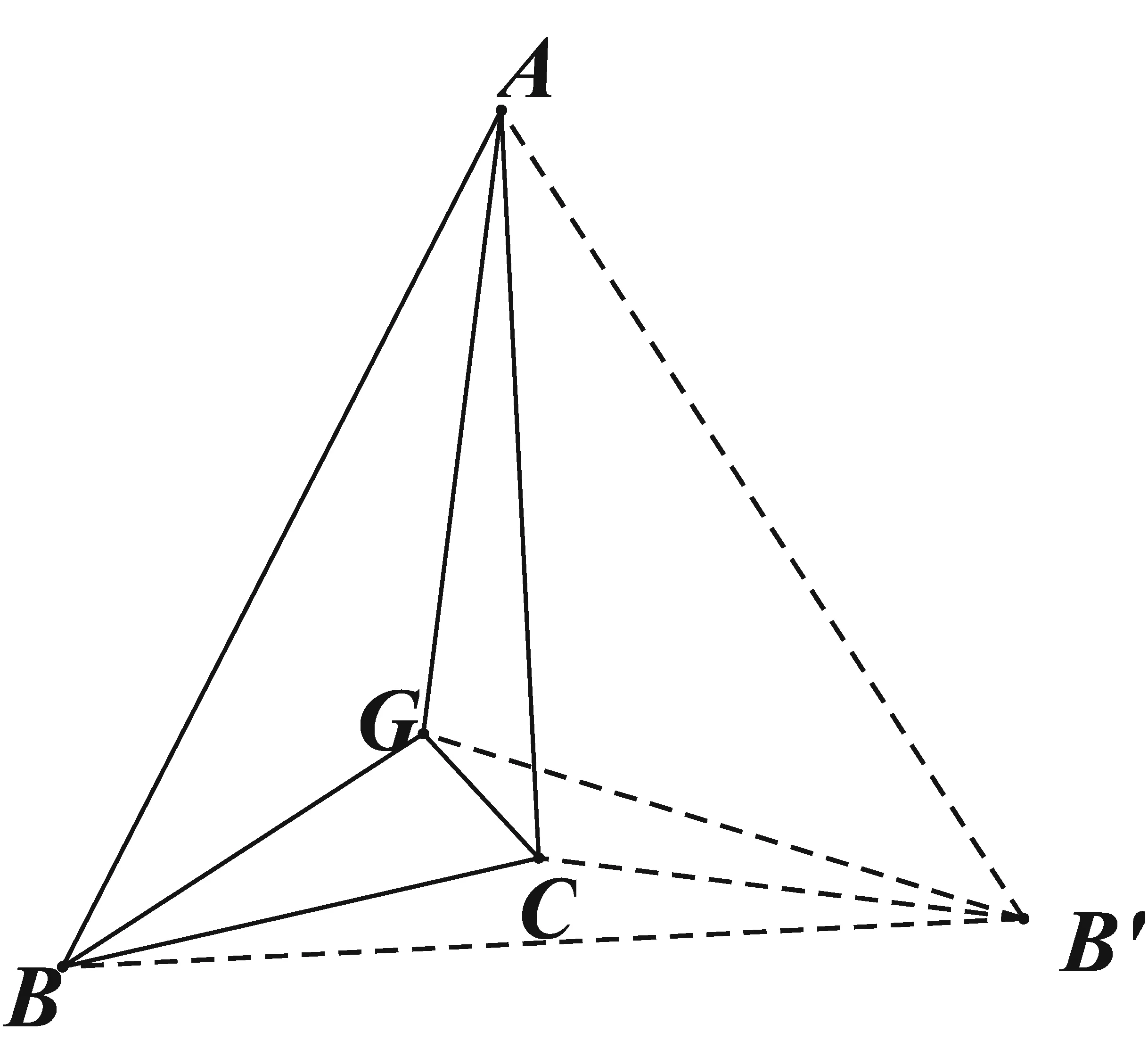
图12

∴∠GAC=∠BAC-∠BAG=10°，

∴∠CGA=180°-∠GAC-∠ACG=130°，

∴∠AB′C+∠CGA=180°

则A、G、C、B′四点共圆，

∴∠AB′G=∠ACG=40°，

又∠GAB′=∠GAC-∠CAB′=40°，

∴∠AB′G=∠GAB′，

∴GB′=GA，

又BB′=BA，

∴△ABG≌△B′BG(sss)，

4 总 结

合同变换对于解决初等几何问题是有重要作用的，本文通过讨论合同变换所包含的三类变换在不同题型中的使用方法，对合同变换在具体问题中的具体应用给出了一定参考，但初等几何问题是无规律可循的，面对这类问题，可以利用合同变换来进行探索研究，但合同变换只是为解决问题提供一个新的思路，具体问题还应具体分析．