创新视角下的立体几何开放题

■江苏省无锡市惠山区教师发展中心 叶亚美

数学开放题，是指无明确条件或结论，必须经过认真分析、探究，方能获解的试题。因能有效考查同学们的思维品质，创造性地分析问题和解决问题，开放题正逐渐成为新高考数学创新命题的新趋势。近年来各地立体几何解答题中开放题的考查形式主要为结构不良试题及探索存在问题。本文拟通过对这两类开放题的解析，为2021届高三数学立体几何复习备考提供一个参考。

创新题型1——结构不良试题:难在策略选择，重在推理严谨

立体几何开放题中结构不良试题多指条件残缺问题。解此类结构不良试题时，需根据题目要求在给定条件中选择部分条件，并利用选定的条件解决相关问题。结构不良试题突出了思维的灵活性及策略选择，能够对数学理解能力、数学探究能力、数学推理能力的考查起到积极的作用。

例1（2020年山东模拟）如图1，在四棱锥P-ABCD 中，PA⊥面ABCD，四边形ABCD 为正方形，F 为线段PC 上的点，过A，D，F 三点的平面与PB 交于点E。在①AB=AP，②BE=PE，③PB⊥FD 三个条件中选两个条件补充到已知条件中，解答下列问题：

（1）求平面ADFE 将四棱锥分成两部分的体积比；

图1

（2）求直线PC 与平面ADFE 所成角的正弦值。

解析：第一种情况：将①AB=AP，②BE=PE 作为已知条件。

（1）设平面ADFE 为平面α。

因为BC∥AD，易证得BC∥平面α，而平面α∩平面PBC=EF，所以EF∥BC。又因为E 为PB 的中点，所以EF 为中位线。

设AP=AB=2，则EF=1。

由PA⊥平面ABCD 得AD⊥PA，又因为AD ⊥AB，所以AD ⊥平面PAB，所以AD⊥AE，所以EF ⊥AE，所以S梯形AEFD=

因为AB=AP，BE=PE，所以PB ⊥AE，AD⊥PB，AD∩AE=A，所以PB⊥平面AEFD，所以

（2）如图2，以A 为坐标原点，AB，AD，AP所在直线为x 轴，y 轴，z轴，建立空间直角坐标系A-xyz，设AB=AD=AP=2，则C（2，2，0），P（0，0，2），B（2，0，0），所以

图2

第二种情况：将①AB=AP，③PB⊥FD作为已知条件。

由AD ⊥AP，AD ⊥AB 知AD ⊥平 面ABP，所以AD⊥PB。又因为PB⊥FD，所以PB⊥平面ADFE，所以PB⊥AE。又因为AB=AP，故E 为PB 的中点，即BE=PE，余下解答同第一种情况。

第三种情况：将②BE=PE，③PB⊥FD作为已知条件。

由PB⊥FD 及第二种情况知PB⊥AE，又BE=PE，易知AB=AP，余下解答仍同第一种情况。

点评：由上述解答可以看到，无论选择哪两个条件，都可解答题目。而且，在选择的三个条件中，并没有哪个选择让解答过程比较繁杂，只要熟练掌握空间点、线、面的关系，严谨推理，都可顺利得到PB⊥平面AEFD 及四边形AEFD 为直角梯形，为求体积比奠定基础。第（2）问通过建立空间直角坐标系，将“求直线PC 与平面ADFE 所成角的正弦值”的问题转化为向量运算，减少了逻辑推理的过程，这种向量运算的方法也是今后求空间角、距离的常用方法。

例2（2020 年山东青岛二模）试在①PC⊥BD，②PC⊥AB，③PA=PC 三个条件中选两个条件补充在下面的横线上，使得PO⊥面ABCD 成立，说明理由，并在此条件下进一步解答该题：如图 3，在四棱锥P-ABCD 中，AC ∩BD=O，四边形ABCD 为菱形，若___，且∠ABC=60°，异面直线PB 与CD所成的角为60°，求二面角A-PB-C 的余弦值。

图3

解析：若选②，由PO⊥面ABCD 知PO⊥AB。又因为PC ⊥AB，所以AB ⊥面PAC，AB ⊥AC，所 以∠BAC=90°，CB ＞BA。这与底面为菱形矛盾，所以②必不选，故选①③。

下面证明PO⊥面ABCD。

因为四边形ABCD 为菱形，所以AC⊥BD。因为PC⊥BD，PC∩AC=C，所以BD⊥面APC。因为PO⊂平面APC，所以BD⊥PO。又因为PA=PC，O 为AC 的中点，所以PO ⊥AC。因为AC ∩BD=O，所以PO⊥面ABCD。

以下略。

点评：由上述解答可以看到，当四边形ABCD 为菱形时，本题所给的条件②是不符合要求的，故能否作出正确判断，并合理选择①③十分关键。当选定条件后，证明PO⊥面ABCD，只需用线面关系进行严谨推理即可。后面的求二面角A-PB-C 的余弦值有两种方法：其一是向量法，即以O 为坐标原点，以OB，OC，OP 所 在直线 为x 轴，y 轴，z 轴，建立空间直角坐标系，通过向量运算求解；其二是直接法，即过点C 作CM ⊥PB 于M，连接AM，可以证明∠CMA 为二面角A-PB-C的平面角，再通过计算求解即可。

创新题型2——探索存在问题:贵有解题思路，成在思想方法

立体几何中的探索存在问题，因“是否存在”的不确定性，增强了试题的开放性。解答探索存在问题时，一般先假定结论存在，并以此进行推理，若能推出矛盾，即可否定假设；或先利用一定的数学思想方法探索存在的可能性，再加以论证。探索存在问题能较好地考查同学们的观察能力、猜想能力、分析判断能力、运算能力等。

例3（2020 年北京丰台区模拟）如图4，在四棱锥M-ABCD 中，AB∥CD，∠ADC = ∠BMC =90°，MB = MC，AD = DC =平面BCM ⊥平面ABCD。

（1）求证：CD∥平面ABM。

（2）求证：AC⊥平面BCM。

（3）在棱AM 上是否存在一点E，使得二面角E-BC-M 的大小为45°? 若存在，求出的值；若不存在，请说明理由。

图4

解析：（1）因 为AB ∥CD，AB ⊂平 面ABM，CD平面ABM，所以CD ∥平 面ABM。

（2）取AB 的中点N，连接CN。

在Rt△CNB 中，由勾股定理得BC=2。

在△ACB 中，由勾股定理逆定理可知AC⊥BC。

又因为平面BCM ⊥平面ABCD，且平面BCM ∩平面ABCD=BC，所以AC⊥平面BCM。

（3）取BC 的中点O，连接OM，ON，所以ON ∥AC。因为AC ⊥平面BCM，所以ON ⊥平面BCM。因为BM=MC，所以OM ⊥BC。

如图5，建立空间直角坐标系O-xyz，则M（0，0，1），B（0，1，0），C（0，-1，0），A（2，-1，0），所以= （- 2，1，1），=（0，-2，0），=（2，-2，0）。

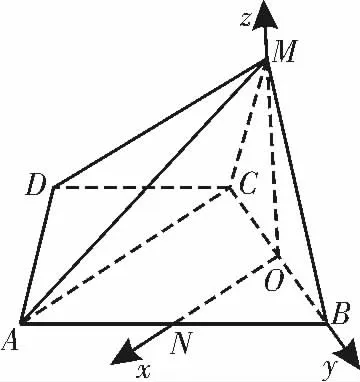
图5

易知平面BCM 的一个法向量为m=（1，0，0）。

假设在棱AM 上存在一点E，使得二面角E-BC-M 的大小为45°。

由题知二面角E-BC-M 为锐二面角，所以在棱AM 上存在一点E，使得二面角E-BC-M 的大小为45°，此时

点评：题（1）（2）只需用空间中线线、线面、面面间的位置关系等基础知识，进行严谨推理即可获证。题（3）由于点E 具有不确定性，通过“假设在棱AM 上存在一点E”，将不确定的问题转化成严格论证探讨的过程，而通过建立平面直角坐标系，又将探索“点E 是否存在”的问题转化为“求符合条件的参数λ 的值”的问题，其解决常常用到方程思想。这种“假设——论证（或求解）”的方法是解决探索存在问题的常用方法。而利用空间向量及待定系数法求解存在性问题显然思路简单、解法固定、操作方便，应引起重视。

例4（2020 年山东聊城模拟）如图6，将长方形OAA1O1（及其内部）绕OO1所在直线旋转一周形成圆柱，其中OA =1，OO1=2，弧的直径。

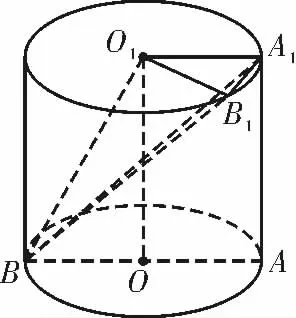
图6

（2）求二面角A1-O1B-B1的余弦值。

解析：（1）存在，当B1C 为圆柱OO1的母线时，BC ⊥AB1。

如图7，连接BC，AC，B1C，因为B1C 为圆柱OO1的母线，所以B1C ⊥平面ABC。又因为BC⊂平面ABC，所以B1C⊥BC。因为AB 为圆O 的直径，所以BC ⊥AC。又因为AC ∩B1C=C，所以BC ⊥平面AB1C。因为AB1⊂平面AB1C，所以BC⊥AB1。

图7

（2）略。

点评：题（1）解决的关键在于利用线面关系确定点C 的位置，确定点C 的思考过程如下：若存在BC⊥AB1，由AB 为直径可知BC⊥AC，则必有BC⊥平面AB1C，从而有BC⊥B1C，又C 在弧上，从而B1C 应为圆柱的母线。题（2）可以通过建立空间直角坐标系，利用空间向量运算求解。

结构不良试题及探索存在问题是近年高考立体几何开放题中的高频考题，充分体现了高考能力立意的指导思想，解决两种开放题，特别要关注求解策略，充分利用向量的工具作用，以及转化思想、方程思想等，请同学们多去探索，去体会，切实提高解题能力。