对称性在积分计算中的运用

尹松庭

（铜陵学院 数学与计算机学院,安徽 铜陵 244000）

0 引言

高等数学介绍了定积分、二重积分、三重积分、第一类曲线积分、第二类曲线积分、第一类曲面积分及第二类曲面积分，而对于每种积分计算都探讨了相关的对称性。由于六种积分分成几个章节先后学习的，因此在课堂上学习积分对称性比较分散，难以统一[1-3]。其次，目前关于探讨各种积分对称性的文献很多，而这类文献在介绍积分对称性时，往往列出各种对称性定理，而且表述繁琐，却极少给出各种对称性的内在联系[4-10]。因此，对于这些数量多内容相似的对称性定理难以区分和牢记，更不能灵活运用。本文将对六种积分的计算进行分类，抓住它们对称性的共性及本质特征，即将对称性分成奇偶与轮换两种，把定积分、二重积分、三重积分、第一类曲线积分、第一类曲面积分归为一大类，而把第二类曲线积分及第二类曲面积归为另外一大类，然后给出“代表性”的对称性定理。

1 奇偶对称性

注：定理1 是以二重积分为例，完全类似的结论对于定积分、三重积分、第一类曲线积分、第一类曲面积分仍然成立。

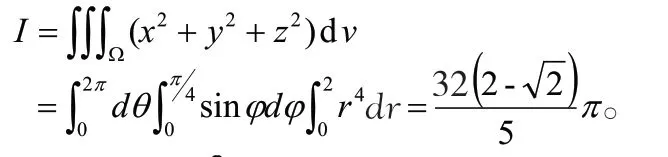
例2计算其中D 为单位圆域在第一象限的部分。

解：用直线将D 分为全等的两部分，则对应点处的坐标分别为根据定理1，函数（表示横坐标减去纵坐标）的积分恰好抵消为零。故

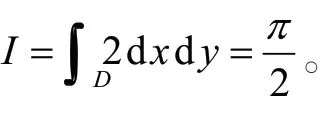
注：定理2是以第二类曲面积分为例。事实上，类似的结论对于第二类曲线积分仍然成立。与定理1 不同在于，第二类曲面（曲线）积分的对称性不仅要考虑被积函数的对称性，还要考虑积分曲面（曲线）的方向性。

例3计算及，其中L 表示半径为圆心在原点的上半圆周,方向为逆时针方向。

解：显然，曲线L 分为左右全等的两部分，且在对应点处被积函数相等。对于，L 的左右两部分方向相反（一个向上一个向下）。故由定理2得出，

这里的第二个等号用到了下面要介绍的轮换对称性。

2 轮换对称性

在定积分计算中，我们熟悉下面的性质

定理3设积分范围具有轮换对称性，表示集合{1,2,3}中任意一个轮换，则函数在上的积分满足

注：如果表达式对于部分坐标是对称的，我们称具有部分轮换对称性。此时可以得到与定理3 相应的结果。具体表述由读者补充。

证明：由于具有轮换对称性，故对于任意的轮换（作用在坐标分量上相当于空间中的一个坐标旋转或镜面反射），总有由于可逆，故

故利用曲线方程化简被积函数可得

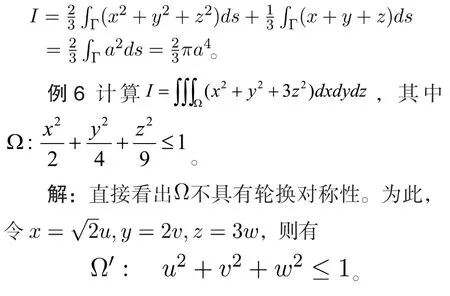
3 总结

本文用三个定理概括了六种积分对称性。这些定理凸显了积分对称性的内在联系和共同特征，且便于记忆，容易掌握。总之，我们要抓住三点：积分范围具有对称性；被积函数在对应点处的值相等或相反；如果涉及第二类积分，要考虑积分范围的方向。