On the length of the longest consecutive switches
-, -,
(School of Mathematics, Sichuan University, Chengdu 610064, China)
Abstract: As a class of simple mathematical models, tossing an unbiased coin independently has extensive applications in many fields. The length of the longest head-run has been long explored by many scholars. Up to now, there is still a lot of results on the extension of this problem and their applications. In this paper, we study the length of the longest consecutive switches and present several limit theorems.
Keywords: Longest head-run; Longest consecutive switches; Limit theorem; Borel-Cantelli lemma
1 Introduction
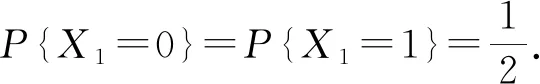
N≥K,N,K∈Ν
(1)
Denote byZNthe largest integer for whichI(N,ZN)=ZN. ThenZNis the length of the longest head-run of pure heads inNBernoulli trials.
The statisticZNhas been long studied because it has extensive applications in reliability theory, biology, quality control, pattern recognition, finance, etc. Erdös and Rényi[1]proved the following result:
Theorem1.1Let 0 Hereafter, we denote by "log" the logarithm with base 2, and by [x] the largest integer which is no more thanx. Theorem 1.1 was extended by Komlós and Tusnády[2]. Erdös and Rényi[3]presented several sharper bounds ofZNincluding the following four theorems among others. Theorem1.2Letεbe any positive number. Then for almost allω∈Ω, there exists a finiteN0=N0(ω,ε) such that ifN≥N0, thenZN≥[logN-log log logN+log log e-2-ε]. Theorem1.3Letεbe any positive number. Then for almost allω∈Ω, there exists an infinite sequenceNi=Ni(ω,ε)(i=1,2,…) of integers such thatZNi<[logNi-log log logNi+log log e-1+ε]. These limit theorems have been extended by many authors. We refer to Guibas and Odlyzko[4], Samarova[5], Révész[6], Nemetz and Kusolitsch[7], Grill[8]and Vaggelatou[9]. The distribution function ofZNand some related problems have been studied by Goncharov[10], Földes[11], Arratiaetal.[12], Novak[13-15], Schilling[16], Binswanger and Embrechts[17], Muselli[18], Vaggelatou[9], Túri[19], Novak[20]. Maoetal.[21]studied the large deviation behavior for the length of the longest head run.For more recent related references, we refer to Asmussenetal.[22], Chen and Yu[23], Li and Yang[24], Pawelec and Urbański[25], and Mezhennaya[26]. In 2012, Anush posed the definition of "switch", and considered the bounds for the number of coin tossing switches. In 2013, Li[27]considered the number of switches in unbiased coin-tossing, and established the central limit theorem and the large deviation principle for the total number of switches. According to Li[27], a "head" switch is the tail followed by a head and a "tail" switch is the head followed by a tail. Motivated by the study of the longest head-run and the work of Li[27], we will study the length of the longest consecutive switches in this paper. At first, we introduce some notations.Form,n∈Ν, define (2) Fori,N∈Ν, define (3) We useA1+A2+…+Aninstead ofA1∪A2…∪Anwhen the setsAi,i=1,…,nare disjoint. The rest of this paper is organized as follows. In Section 2, we present main results. The proofs will be given in Section 3. In Section 4, we give some final remarks. In this section, we present several limit results onMN. Corresponding to Theorems 1.1~1.5, we have the following five theorems. Theorem2.1We have (4) Theorem2.2Letεbe any positive number. Then for almost allω∈Ω, there exists a finiteN0=N0(ω,ε) such that ifN>N0, MN≥[logN-log log logN+ (5) Theorem2.3Letεbe any positive number. Then for almost allω∈Ω, there exists an infinite sequenceNi=Ni(ω,ε)(i=1,2,…) of integers such that MNi<[logNi-logloglogNi+ (6) The last two theorems can be reformulated as follows. Remark 2 The closely related result with respect to Theorems 2.4 and 2.5 is Guibas and Odlyzko[4](Theorem 1). which together with the Borel-Cantelli lemma implies that It follows that (7) LetkT He looked at me. I knew you were going to ask that, he said. I m going to be a dancer someday. He pointed to the administration building. My bosses are in there, and they re paying for my training. Mn≤M(k+1)T≤(1+ε)log(k+1)T≤ (1+2ε)logkT≤(1+2ε)logn Now we turn to the proofs for Theorems 2.2, 2.3, 2.4*and 2.5*.The basic idea of these comes from Ref.[7]. For the reader's convenience, we spell out the details. At first, as in Ref.[7, Theorem 5], we give an estimate for the length of consecutive switches, which is very useful in our proofs. Theorem3.1LetN,K∈Νand letMNbe defined in (3) withi=1. Then, ifN≥2K, then (8) To prove Theorem 3.1, we need the following lemma. (9) A={M2N≥N-1}, Then we have (10) and Hence ProofofTheorem3.1LetN,K∈ΝwithN≥2K. Denote Let (11) (12) Similarly we have (13) By the obvious fact thatD0⊂{MN≥K-1}, we get that (14) Fori=1,…,K+1, denoteFi={(Xi,…,Xi+K-1)is the first section of consecutive switches of lengthK-1 in the sequence (Xi,…,X2K)}.Then we have and By the independence of {Xj,j=1,2,…,N}, we have P(D1F1)=P(D1)P(F1) (15) P(D1F2)= P(D1∩{(X2,…,XK+1)} has consecutive switches,X1=X2})= P(D1∩{(X2,…,XK+1)} has consecutive switches,X1=X2,XK+1=1})+ P(D1∩{(X2,…,XK+1)} has consecutive switches,X1=X2,XK+1=0})= 2P(D1∩{(X2,…,XK+1)} has consecutive switches,X1=X2,XK+1=1})= 2P(D1∩{XK+1=1})P{(X2,…,XK) has consecutive switches,XK=0,X1=X2})= (16) P(D1F3)=(suppose thatK≥3) P(D1∩{(X3,…,XK+2)} has consecutive switches,X2=X3})= P(D1∩{(X3,…,XK+2)} has consecutive switches,X2=X3,(XK+1,XK+2)=(0,1)})+ P(D1∩{(X3,…,XK+2)} has consecutive switches,X2=X3,(XK+1,XK+2)=(1,0)})= 2P(D1∩{(X3,…,XK+2)} has consecutive switches,X2=X3,(XK+1,XK+2)=(0,1)})= 2P({(X3,…,XK) has consecutive switches, XK=1,X2=X3})×P(D1∩{(XK+1,XK+2)= (0,1)})=4P(D1∩{(XK+1,XK+2)= (0,1)})P(F3) (17) By the definition ofD1, we know that P(D1∩{(XK+1,XK+2)=(0,1)})≥ P(D1∩{(XK+1,XK+2)=(0,0)}), P(D1∩{(XK+1,XK+2)=(0,1)})≥ P(D1∩{(XK+1,XK+2)=(1,1)}), P(D1∩{(XK+1,XK+2)=(0,1)})= P(D1∩{(XK+1,XK+2)=(1,0)}), which together with (17) implies that P(D1F3)-P(D1)P(F3)= {P({(XK+1,XK+2)=(0,1)}∩D1)- P({(XK+1,XK+2)=(0,0)}∩D1)+ P({(XK+1,XK+2)=(0,1)}∩D1)- P({(XK+1,XK+2)=(1,1)}∩D1)}P(F3)≥0 (18) Similarly, ifK≥4, we have that P(D1Fi)≥P(D1)P(Fi),∀i=4,…,K (19) Finally, by the definitions ofD1andFK+1, we know thatD1∩FK+1=FK+1. Hence we have P(D1FK+1)=P(FK+1)≥P(D1)P(FK+1) (20) By (15), (16), (18), (19) and (20), we obtain It is easy to check that Then by (12) and (13), we get (21) As to the right-hand side of (21), we have Hence (22) By (14) and (22), we complete the proof. To prove Theorem 2.2, we need the following lemma. ProofWe have Ifa<2, thenp=loga<1 and thus Then by Theorem 3.1, we have (23) Without loss of generality, we assume thatej≥2 for anyj>M.Byα1(Nj)+1=j, we have j≤logNj-logloglogNj+logloge-1-ε and thus Thus To prove Theorem 2.3, we need the following version of Borel-Cantelli lemma. (24) ProofofTheorem2.3Letδ>0. LetNj=Nj(δ) be the smallest integer for whichα2(Nj)=[j1+δ] withα2(Nj) given by (6). Define {MNj<([j1+δ]+1)-1},j≥1 (25) By Theorem 3.1, we have (26) (27) Then there existsM∈Νsuch thatM>2 and fj≥2,∀j>M (28) By (6) we have logNj-logloglogNj+logloge+ε≤[j1+δ]+1, which implies that Then by (26) and (28), we get (29) Let 0<ε<1 satisfy [j1+δ]=[logNj-logloglogNj+logloge+ε] >ε0logNj,∀j=1,2,…. (30) Hence we have (31) For any given positive numberε, by (27), we have (32) Recall that {Aj,j≥1} is defined in (25). Fori We claim that P(Aj)=P(Bi,j)P(Ci,j)(1+o(1)), i (33) In fact, by the definitions ofAj,Bi,jandCi,j, we know that α2(Nj)}. Then (33) is equivalent to (34) By the definition ofCi,j, we get that α2(Nj)}|Bi,j∩Ci,j)= α2(Nj)]|Bi,j∩Ci,j)≤ α2(Nj)]|Bi,j∩Ci,j)≤ (35) By Theorem 3.1, we have that whenjis large enough, (36) asj→∞. WhenNi≥α2(Nj) andi (37) Similar to (33), we have P(AiAj)=P(Ai)P(Ci,j)(1+o(1)), i (38) By (33) and (38), we get i which together with (37) implies that 1+o(1),i (39) Then we get that (34) holds and thus by Lemma 3.4 we complete the proof. After the first version of our paper was uploaded to arXiv, Professor Laurent Tournier sent two emails to us and gave some helpful comments. In particular, he told us one way to reduce consecutive switches to pure heads or pure tails by doing the following: introduce a sequence (Yn) such thatY2n=X2n,Y2n+1=1-X2n+1. Then (Yn) is again a sequence of independent and unbiased coin tosses. And a sequence of consecutive switches forXis equivalent to a sequence of pure heads or pure tails forY. Then Theorems 2.1 and 2.5 can be deduced easily from Theorems 1.1 and 1.5, respectively. We spell out all the proofs with two reasons. One is for the reader's convenience. The other is that as to biased coin tosses, it seems that Theorems 2.1 and 2.5 can not be deduced directly from Theorems 1.1 and 1.5, respectively, and our proof may be moved to that case. We will consider the biased coin tosses in a forthcoming paper.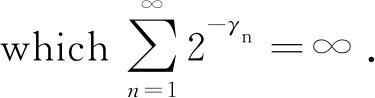
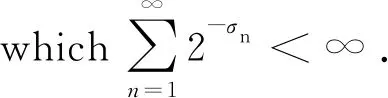
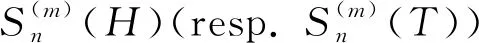
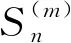
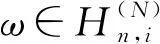
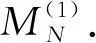
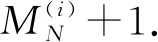
2 The main results


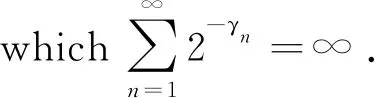

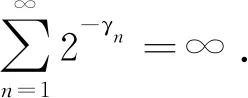

3 The proofs of the main results
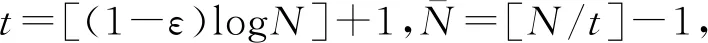

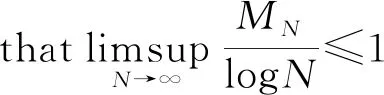
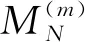
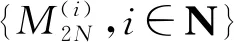
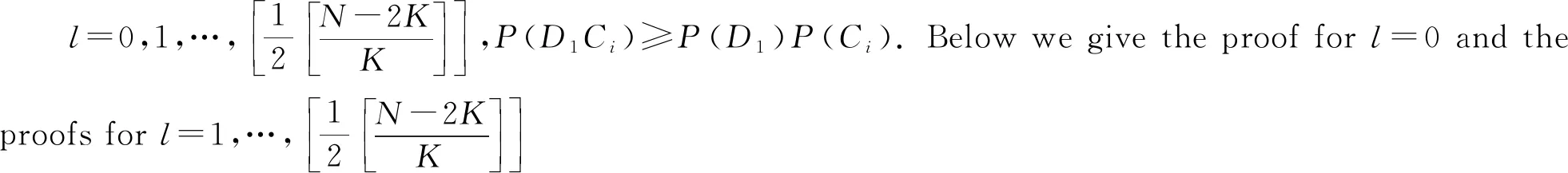
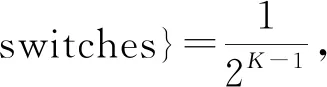

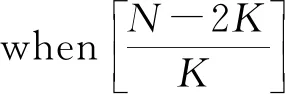
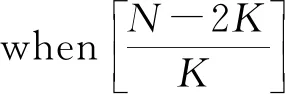
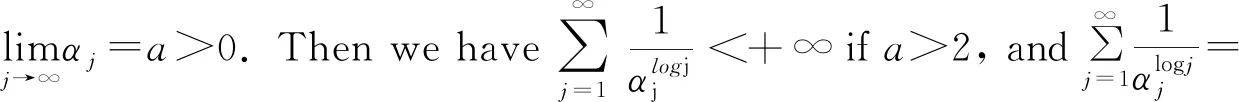
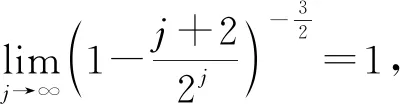
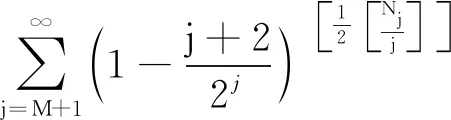

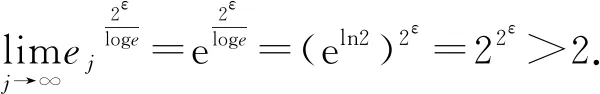
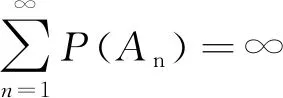



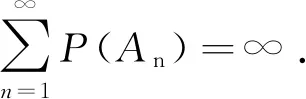
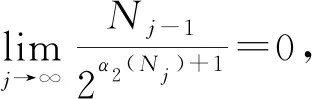
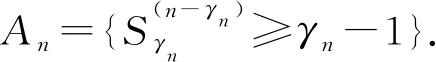
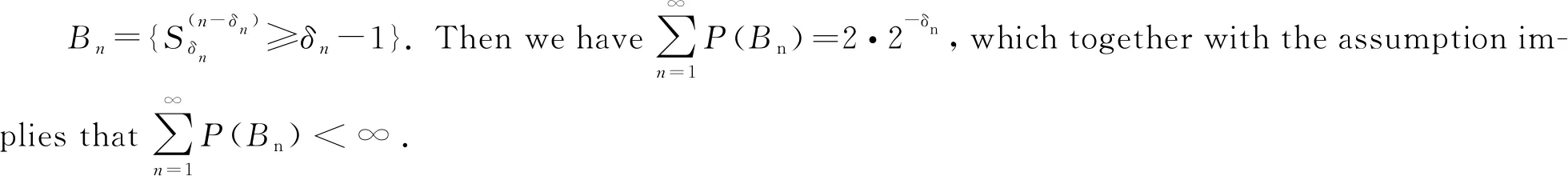
4 Final remark

