一类不定权弹性梁方程的正解

杨 丽 娟

(西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

梁方程是一类重要的四阶微分方程, 在弹性力学和工程物理等领域应用广泛, 关于其可解性的研究目前已有许多成果[1-10]. 例如, Li[1]用锥上不动点定理, 研究了问题

(1)

正解的存在性, 其中f: [0,1]×[0,∞)→[0,∞)为连续函数,ρ,τ∈满足

记

定理1[1]若下列条件之一成立：

则问题(1)至少存在一个正解.

文献[1]中问题(1)正解的存在性是在非线性项f为正情形下得到的.Hai[11]用Leray-Schauder不动点定理, 研究了椭圆问题

正解的存在性, 其中Ω为N上边界光滑的有界区域, 非线性项f和权函数a均可正可负； Ma[12]用相同方法研究了一端固定、 一端自由的梁方程

正解的存在性.受文献[11-12]的启发, 本文在f,a满足文献[11]的条件下, 讨论方程线性部分更一般的梁方程

(2)

正解的存在性, 其中边界条件表示梁的两端简单支撑.

本文总假设：

(H1)α,β∈且

(H2)f:+→连续函数且f(0)>0.

1 预备知识

根据条件(H1)易知μ1≥μ2>-π2.令gi(t,s)(i=1,2)是线性边值问题

的Green函数.

引理1对任意的t,s∈(0,1),gi(t,s)>0,i=1,2.

若μi=0, 则gi(t,s)可表示为

若-π2<μi<0, 则gi(t,s)可表示为

由gi(t,s)的表达式易得gi(t,s)>0于t,s∈(0,1).

令h∈X, 则线性边值问题

(3)

存在唯一解

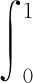
事实上, 由于

因此问题(3)的解可表示为

交换积分次序后令

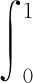
即可.

引理2(Leray-Schauder不动点定理)[13]设E是Banach空间, 算子T:E→E全连续, 若集合

{‖x‖|x∈E,x=θTx, 0<θ<1}

有界, 则T在闭球A⊂E中必存在不动点, 其中

A={x|x∈E, ‖x‖≤R},R=sup{‖x‖|x=θTx, 0<θ<1}.

(4)

这里a+(t)=max{0,a(t)}为a的正部,a-(t)=max{0,-a(t)}为a的负部.

设S为X中的有界集, 即存在正数B, 使得对任意的u∈S, ‖u‖≤B.由f的连续性知, 必存在M>0, 使得

|f(u)|≤M,u∈S.

于是对任意的t∈[0,1], 有

(5)

(6)

即

2 主要结果

假设:

(H3)a: [0,1]→连续且在(0,1)的任一子区间内不恒为0, 并存在常数k>1, 使得

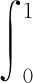
定理2假设条件(H1)～(H3)成立, 则存在λ0>0, 使得当0<λ<λ0时, 问题(2)存在一个正解.

|f(u)|q(t)≤γf(0)p(t).

(7)

固定δ∈(γ,1), 并设λ0>0, 使得对任意的λ<λ0, 有

(8)

(9)

(10)

对每个w∈X, 令v=Hw, 其中

显然H:X→X全连续.令v∈X, 使得v=θHv,θ∈(0,1), 则

且‖v‖≠λδf(0)‖p‖.若不然, 设‖v‖=λδf(0)‖p‖, 由式(8), 有

由于

根据式(9), 可得

再结合式(7)和式(9)知, 对任意的t∈[0,1], 有

因此

与假设矛盾, 故‖v‖≠λδf(0)‖p‖.再由式(8), 有‖v‖≯λδf(0)‖p‖, 因此‖vλ‖<λδf(0)‖p‖.根据引理2,H有一个不动点vλ.

由于对任意的t∈[0,1], 有

故uλ是问题(2)的一个正解.

3 应用实例

例1考虑四阶问题

(12)

正解的存在性, 其中λ是一个正参数.

取k=2, 通过简单计算可得

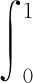
因此

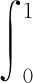
成立, 满足条件(H3).根据定理2可知, 存在λ0>0, 使得当0<λ<λ0时, 问题(2)存在一个正解.