低维Hom-Jacobi-Jordan代数的分类

李 小 朝

(黄淮学院 数学与统计学院, 河南 驻马店 463000)

1 引言与预备知识

Hom-代数是一类更广泛的代数结构, 目前已得到广泛关注： 文献[1-2]将李代数的Jacobi等式通过线性映射进行形变得到了Hom-李代数, Hom-李代数可视为通常李代数的一种形变或推广； Hu[3]给出了李代数形变的q-李代数； 文献[4-6]研究了Hom-李代数的结构和低维分类等； 文献[7-8]分别在低维Leibniz代数分类和低维Poisson代数分类的基础上, 利用待定系数法给出了低维Hom-Leibniz代数分类和低维Hom-Poisson代数分类. 文献[9]通过将向量空间L上李代数的反对称性条件[x,y]=-[y,x]换为对称性条件[x,y]=[y,x](∀x,y∈L), 给出了Jacobi-Jordan代数的概念, 指出Jacobi-Jordan代数是一类特殊的Jordan代数, 并给出了其低维分类； 文献[10]将Jordan代数的研究推广到δ-Jordan李超代数上, 研究了带有对称根系的任意分裂δ-Jordan李超代数的结构； 文献[11]给出了二次Hom-Leibniz代数的概念， 并研究了其若干重要性质; 文献[12]考虑满足Jacobi等式的交换代数——Mock李代数, 即Jacobi-Jordan代数. Jacobi-Jordan代数可通过反结合代数, 即满足(xy)z+x(yz)=0的代数, 类似于结合代数构造李代数的方法实现. 类似于文献[1-2,4]构造Hom-李代数的方法, 本文将Jacobi-Jordan代数的Jacobi等式通过线性映射进行扭曲, 给出Hom-Jacobi-Jordan代数, 并利用待定系数法, 给出低维Hom-Jacobi-Jordan代数的分类.

定义1[9]设L是数域K上的向量空间, 二元运算[,]:L×L→L是双线性的, 满足[x,y]=[y,x]和Jacobi等式： ∀x,y,z∈L, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0.则称(L,[,])是一个Jacobi-Jordan代数.

定义2设(L,[,],α)是一个三元组, 其中L是数域K上的向量空间,α:L→L是一个线性映射, 二元运算[,]:L×L→L是双线性的, 若对∀x,y,z∈L, 满足下列条件:

1) [x,y]=[y,x];

2) [α(x),[y,z]]+[α(y),[z,x]]+[α(z),[x,y]]=0.

则称(L,[,],α)是一个Hom-Jacobi-Jordan代数. 条件2)称为Hom-Jacobi等式.若还满足α是自同态：α([x,y])=[α(x),α(y)], 则称(L,[,],α)为保积Hom-Jacobi-Jordan代数.

注1当α是恒等变换时, Hom-Jacobi-Jordan代数即为Jacobi-Jordan代数.

定义3设(L,[,],α)为Hom-Jacobi-Jordan代数.若L的子空间L1满足α(L1)⊆L1,[L1,L1]⊆L1, 则称(L1,[,],α|L1)是(L,[,],α)的Hom-子代数.若L的子空间L2满足α(L2)⊆L2, [L2,L]⊆L2, 则称(L2,[,],α|L2)是(L,[,],α)的Hom-理想.

定义4设(L1,[,]1,α1)和(L2,[,]2,α2)是两个Hom-Jacobi-Jordan代数,f:L1→L2是一个线性映射.若对∀x,y∈L1, 均有f([x,y]1)=[f(x),f(y)]2和f∘α1=α2∘f, 则称f是一个Hom-Jacobi-Jordan代数同态.特别地, 若f是可逆的线性映射, 则称f是一个Hom-Jacobi-Jordan代数同构, 且(L1,[,]1,α1),(L2,[,]2,α2)是同构的.

注2若Hom-Jacobi-Jordan代数(L1,[,]1,α1)和(L2,[,]2,α2)同构, 则线性映射α1和α2相似.

命题1设(L,[,])是一个Jacobi-Jordan代数,α:L→L是L的自同态.∀x,y∈L, 令[x,y]α=α([x,y]), 则(L,[,]α,α)是一个保积Hom-Jacobi-Jordan代数.

证明： 由于α([x,y])=[α(x),α(y)], 因此

[α(x),[y,z]α]α=α([α(x),α([y,z])])=α2([x,[y,z]]),

结论易证.

命题2设(L,[,],α)是一个保积Hom-Jacobi-Jordan代数,α是可逆的.∀x,y∈L, 令[x,y]α-1=α-1([x,y]), 则(L,[,]α-1)是一个Jacobi-Jordan代数.

证明： 由于α([x,y])=[α(x),α(y)]和α可逆, 故有α-1([x,y])=[α-1(x),α-1(y)], 从而可得

因此(L,[,]α-1)是一个Jacobi-Jordan代数.

注3保积Hom-Jacobi-Jordan代数(L,[,],α)(α可逆)均可由Jacobi-Jordan代数及其自同构利用命题1的方法得到.

定义5设(L1,[,],α1),(L2,[,],α2)是Hom-Jacobi-Jordan代数(L,[,],α)的理想, 且L有线性子空间的直和分解L=L1+L2, 则称(L,[,],α)为理想(L1,[,],α1)和(L2,[,],α2)的直和, 记为(L,[,],α)=(L1,[,],α1)⊕(L2,[,],α2).

2 主要结果

文献[9]在同构意义下给出了低维Jacobi-Jordan代数的分类. 因此, 本文给出的低维Hom-Jacobi-Jordan代数分类, 都不是Jacobi-Jordan代数. 用span(x1,x2,…,xk)表示向量空间L中元素x1,x2,…,xk生成的子空间.

引理1[9]设(L,[,])为Jacobi-Jordan代数, 则在同构意义下, 有:

1) 二维Jacobi-Jordan代数有J20: [xi,xj]=0(i,j=1,2)和J21: [x1,x1]=x2；

2) 三维Jacobi-Jordan代数有J30: [xi,xj]=0(i,j=1,2,3),J31: [x1,x1]=x2和J32: [x1,x1]=x2, [x3,x3]=x2(本文未给出的括积均为0, 下同).

定理1设(L,[,],α)为保积Hom-Jacobi-Jordan代数, 若α=0, 则：

证明： 由于α=0, 则有α(x)=0(∀x∈L), 即Hom-Jacobi等式成立.因此只需L中某些元素不满足Jacobi等式.证毕.

下面给出的保积Hom-Jacobi-Jordan代数(L,[,],α)都是α非零的情形.

证明： 设[x1,x1]=ax1,α(x1)=bx1, 由Hom-Jacobi等式可得3a2bx1=0.由于α非零, 因此有b≠0, 从而可得a=0, 即[x1,x1]=0, 证毕.

定理3设(L,[,],α)为二维保积Hom-Jacobi-Jordan代数,x1,x2是L的一组基, 则在同构意义下, 有:

证明： 设

[x1,x1]=a11x1+a12x2, [x1,x2]=a21x1+a22x2, [x2,x2]=a31x1+a32x2,

再设α在基x1,x2下的矩阵为B=(bij)2×2.由定义4知, 只需考虑矩阵B对应的Jordan标准形即可.

定理4设(L,[,],α)为三维保积Hom-Jacobi-Jordan代数,x1,x2,x3是L的一组基,α的秩为3, 则Hom-Jacobi-Jordan代数(L,[,],α)也是Jacobi-Jordan代数.

证明： 由于α的秩为3, 则α是可逆的.由命题1和命题2知, 只需对Jacobi-Jordan代数求出自同构, 利用命题1的方法即可构造Hom-Jacobi-Jordan代数.

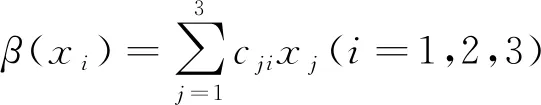
对J32: [x1,x1]=x2, [x3,x3]=x2同理可证.证毕.

定理5设(L,[,],α)为三维保积Hom-Jacobi-Jordan代数,x1,x2,x3是L的一组基,α的秩为2, 则在同构意义下, 有:

1) 对B1,B2, 由于α是自同态, 即α([xi,xj])=[α(xi),α(xj)](i,j=1,2,3), 可得

a13=a23=a33=a41=a42=a51=a52=a61=a62=0.

由x2,x2,x3满足Hom-Jacobi等式, 可得a53=0.再由x1,x1,x3满足Hom-Jacobi等式, 可得a43=0.即有

[x1,x1]=a11x1+a12x2, [x1,x2]=a21x1+a22x2, [x2,x2]=a31x1+a32x2,

[x1,x3]=[x2,x3]=0, [x3,x3]=a66x3.

令x1,x2和x3生成的子空间分别为L1=span(x1,x2)和L2=span(x3),α1=α|L1,α2=α|L2=0, 则(L1,[,],α1)和(L2,[,],α2)均为(L,[,],α)的理想, 即有(L,[,],α)=(L1,[,],α1)⊕(L2,[,],α2).

因此有(L,[,],α)≅(J20,[,]β1,β1)⊕(L2,[,],α2)或(L,[,],α)≅(J21,[,]β2,β2)⊕(L2,[,],α2), 当a66≠0时, (L,[,],α)不是Jacobi-Jordan代数.

3) 对B4同理可得.证毕.

定理6设(L,[,],α)为三维保积Hom-Jacobi-Jordan代数,x1,x2,x3是L的一组基,α的秩为1, 则在同构意义下, 有:

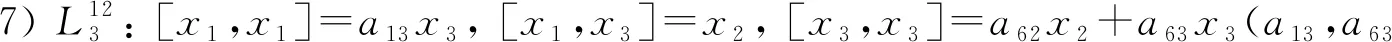
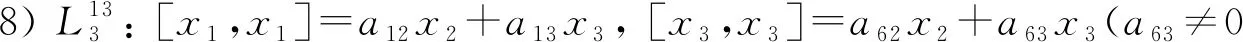
1) 对B5, 由于α是自同态, 即α([xi,xj])=[α(xi),α(xj)](i,j=1,2,3), 可得a12=a13=a21=a31=a41=a51=a61=0.由x1,x1,x1满足Hom-Jacobi等式, 可得a11=0.再由x1,x1,x2满足Hom-Jacobi等式, 可得

a22a22+a42a23=0,a23a22+a43a23=0.

(1)

同理由xi,xj,xk(i,j,k=1,2,3)满足Hom-Jacobi等式, 分别可得

a22x+a42y=0,a23x+a43y=0

(6)

的解.

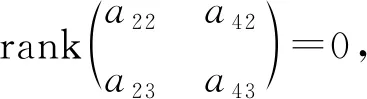
令子空间L1=span(x1),L2=span(x2,x3),α1=α|L1≠0,α2=α|L2=0, 则(L1,[,],α1)和(L2,[,],α2)都是(L,[,],α)的理想, 即有

[x1,x3]=x2, [x2,x2]=a32x2, [x2,x3]=a52x2, [x3,x3]=a62x2.

易验证当a32,a52不全为0时, 所得的Hom-Jacobi-Jordan代数不是Jacobi-Jordan代数.

2) 对B6, 由于α是自同态, 即α([xi,xj])=[α(xi),α(xj)](i,j=1,2,3), 可得a21=a31=a41=a51=a61=a33=0,a11=a32.由x1,x2,x2满足Hom-Jacobi等式, 可得a32=0, 进而有a11=0.由x1,x2,x3满足Hom-Jacobi等式, 可得a53=0.再由其他元素满足Hom-Jacobi等式, 可得a52a13=a52a23=a52a43=a52a63=0.

① 若a52≠0, 则有a13=a23=a43=a63=0.再经过适当的基变换, 可得[x1,x1]=a12x2, [x2,x3]=x2, 其他括积均为0.易验证x2,x3,x3不满足Jacobi等式, 即所得的Hom-Jacobi-Jordan代数不是Jacobi-Jordan代数.

② 若a52=0, 则有[x2,x2]=0, [x2,x3]=0.下面讨论a22,a23的取值情况.

(i) 当a22≠0时, 做适当的基变换, 把a12和a42化为0, 则得

[x1,x1]=a13x3, [x1,x2]=a22x2+a23x3(a22≠0),

[x1,x3]=a43x3, [x3,x3]=a62x2+a63x3.

易验证x1,x1,x2不满足Jacobi等式.

(ii) 当a22=0,a23≠0时, 做适当的基变换, 把a23化为1,a13和a43化为0, 则可得

[x1,x1]=a12x2, [x1,x2]=x3, [x1,x3]=a42x2, [x3,x3]=a62x2+a63x3.

易验证当a12,a42,a62,a63不全为0时, 所得的Hom-Jacobi-Jordan代数不是Jacobi-Jordan代数.

(iii) 当a22=a23=0时, 讨论a42,a43, 分别可得不是Jacobi-Jordan代数的Hom-Jacobi-Jordan代数

[x1,x1]=a12x2, [x1,x3]=a42x2+a43x3(a43≠0), [x3,x3]=a62x2+a63x3,

[x1,x1]=a13x3, [x1,x3]=x2, [x3,x3]=a62x2+a63x3(a13,a63不全为0),

[x1,x1]=a12x2+a13x3, [x3,x3]=a62x2+a63x3(a63≠0或者a13a62≠0).

证毕.