一类各向异性非牛顿微极流体方程组弱解的存在性
王长佳, 石绍力
(长春理工大学 理学院, 长春 130022)
0 引 言
在三维空间中考虑如下一类各向异性非牛顿微极流体方程组的初边值问题:

(1)
其中:Ω⊂3为一边界充分光滑的有界区域,QT=Ω×[0,T],ΓT=∂Ω×[0,T]; 未知向量函数u=(u1,u2,u3)表示流体速度,w=(w1,w2,w3)表示角速度,P表示压力,f=(f1,f2,f3),g=(g1,g2,g3)为给定的外力项,Diu=(∂iu1,∂iu2,∂iu3); 指数qi为给定的常数, 满足1 微极流体方程是一类重要的偏微分方程, 在数学和物理中应用广泛, 可描述一些经典Navier-Stokes方程无法处理的黏性不可压缩流体的物理现象, 如动物血液的流动等. Araújo等[1]在具有Dirichlet边界条件三维空间的有界光滑域中, 利用Faedo-Galerkin和紧致性论证的方法, 证明了非牛顿微极流体模型解的唯一性和周期性. 对于各向异性非牛顿流体, Antontsev等[2]研究了一类具有各向异性扩散的不可压缩Navier-Stokes方程的演化问题, 证明了其第一初边值问题弱解的存在性. 令q=(q1,q2,…,qN), 1 Lq(Ω)={u|u∈Lqi(Ω),i=1,2,…,N}, W1,q(Ω)={u|u∈W1,1(Ω),Diu∈Lqi(Ω),i=1,2,…,N}, 分别赋予范数 则其成为完备的线性赋范空间, 即Banach空间. 记β=max{q1,q2,…,qN},α=min{q1,q2,…,qN}, 为讨论方便, 本文假设指数qi满足α=q1≤q2≤…≤qN=β. 引理1[3]令Ω⊂N为一边界充分光滑的有界开集.如果则如下嵌入关系成立: (2) (3) 注1由引理1, 本文假设指标qi(i=1,2,3)满足条件1/q1+1/q2+1/q3>1. 下面考虑抛物型各项异性空间.令 (4) 2)u(0)=u0,w(0)=w0; 3) 对∀φ∈Vq∩Lθ(Ω),φ∈L2(Ω)以及a.e.t∈[0,T], 有 注2在弱解定义1中未包含压力项P.事实上, 若定义1中条件1),3)成立, 则由Rham定理知, 存在函数P∈L2(Ω)在广义函数意义下满足上述积分等式[4]. 注3定义1中,u(0)=u0,w(0)=w0在下列意义下成立: (5) (6) (7) 引理3[4]设X,Y为两个Banach空间,X连续嵌入到Y.如果函数u∈L∞(0,T;X)且u: [0,T]→Y是弱连续的, 则u: [0,T]→X是弱连续的. 定理1设Ω⊂3为一个边界充分光滑的有界开集,若则问题(1)至少存在一对弱解(u,w), 满足 u∈CW([0,T];H)∩Lq(0,T;Vq),w∈CW([0,T];L2(Ω))∩L2(0,T;H01(Ω)), 其中: (8) u∈CW([0,T];X)表示u: [0,T]→X是弱连续的. 下面证明定理1. (9) 寻求问题(1)如下形式的近似解: 并且当m→∞时, um(0)=u0m→u0于H;wm(0)=w0m→w0于L2(Ω). (12) (15) 利用引理2、 Hölder不等式与Young不等式, 整理式(15)可得 将式(16),(17)相加, 并整理得 将式(18)在(0,t)(0≤t≤T)上积分, 可得 又对∀φ∈Lqi(0,T;Vqi(Ω)), 有 利用估计式(20)可知 (22) 下面推导Ji(i=1,2,3,4,5)的估计. 对J2项, 利用引理2可得 对J3项有 对J4项, 利用式(15)有 (27) 对J5项有 (28) (29) 在广义函数意义下, 将式(11)重写为 (30) 下面逐项推导Ii的估计. 对I2项有 由式(20)知wm∈L2(0,T;W1,2(Ω))∩L∞(0,T;L2(Ω)), 故由文献[8]中引理2.3.3知,wm∈L4(0,T;L3(Ω)), 从而 (32) 对I3项有 由式(15), 对I4项有 对I5项有 (35) 综合式(32)~(35)并利用式(20)可得 (36) 由式(20),(22),(29),(36)可得下列收敛性: um→u强收敛于Lα(0,T;H), (38) 从而由式(20),(38)并利用插值定理可得 um→u强收敛于Lσ(0,T;H), ∀σ≥1. (39) wm→w强收敛于L2(0,T;L2(Ω)). (40) 由上述收敛性, 在式(10),(11)中令m→∞取极限, 可得 当φ∈Vq,u∈L∞(0,T;H)∩Lq(0,T;Vq)时, 有 (43) 下面只需证明 (46) 由于对∀ξ,η∈Lq(0,T;Vq),ξ≠η, 有 即Ai,A为单调算子, 因此可利用单调性方法证明式(46)成立. (47) 由α的定义及引理1知 于是由插值公式有 其次, 类似于文献[6]中方法可知, 对a.e.t∈(0,T), 有 对∀η∈Lq(0,T;Vq), 令 由A的单调性可知 (49) 由式(10)可知 令m→∞, 得 结合式(48),(49)可知 (50) 对任意的λ≥0,ξ∈Lq(0,T;Vq), 取η=u-λξ, 代入式(50)得 (51) 在式(51)中令λ→0取极限, 得 故S=A(u), a.e.(x,t)∈QT.定理1得证.1 预备知识










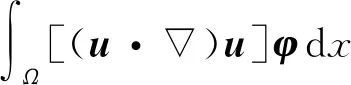



2 主要结果

2.1 近似解的构造




2.2 一致性先验估计

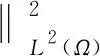














2.3 近似解的收敛性和存在性证明













