一类拟线性Choquard方程非平凡解的存在性

孙雪琪, 宋玥蔷

(长春师范大学 数学学院, 长春 130032)

1 引言与主要结果

拟线性Schrödinger方程[1]

-Δu+V(x)u-[Δ(u2)]u=h(x,u),x∈N

(1)

来源于数学物理中的许多模型, 关于其解的存在性与多解性研究目前已得到广泛关注[2-8]. 文献[2]通过一个变量替换, 将拟线性问题转化为半线性问题, 并利用山路引理证明了方程(1)正解的存在性； 文献[3]用相同的变量替换及对偶方法研究了一类不同的非线项方程; 文献[4]利用扰动方法和Nehari方法研究了一类拟线性椭圆方程, 并得到了变号解和基态解的存在性. 另一方面, 关于Choquard方程[5]

(2)

解的存在性和定性性质研究也很广泛[6]. 对于问题(1)-(2), 文献[9]考虑如下拟线性Choquard方程:

利用扰法方法得到了其正解、 负解和高能量解的存在性. 但当p≠2时, 对于带有p-Laplace算子和卷积项方程的研究目前尚未见文献报道.

本文利用山路引理讨论如下拟线性Choquard方程

(3)

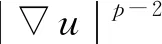
本文主要结果如下:

本文所研究问题的主要难点如下:

1) 由于出现非齐次项Δp(u2)u, 因此一般的临界点理论无法直接应用到相应的能量泛函上, 本文通过引入类似文献[2]的变量替换u=f(v), 将原问题转化到合适空间上进行讨论;

2) 方程(1)中的卷积项导致紧性条件不再成立, 本文利用一些精细的分析技巧解决了该问题.

2 预备知识

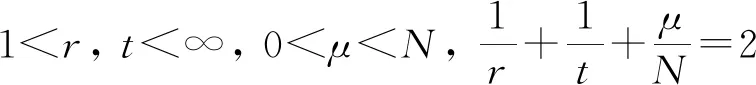
方程(3)对应的能量泛函为

但泛函J在空间

D1,p(N)∶={u∈Lp*(N):u∈Lp(N)}

上无定义, 为克服该困难, 本文采用类似文献[2]的方法, 做变量变换v=f-1(u), 当t∈[0,+∞)时, 函数f由下列方程确定:

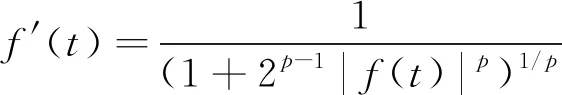
当t∈(-∞,0]时,f(t)=-f(-t).

函数f具有下列性质[3,11]:

(i) 对任意的t∈, |f′(t)|≤1;

(ii) 对任意的t∈, |f(t)|≤|t|;

(iv) 对任意的t∈, |f(t)|≤21/(2p);

(vii) 存在正常数C, 使得当|t|≤1时, |f(t)|≥C|t|; 当|t|≥1时, |f(t)|≤C|t|.

于是, 能量泛函J可改写为

其中J在空间D1,p(N)上有定义, 利用文献[12]的证明方法可证J∈C1(D1,p(N),).

定理2(山路引理)[10]设X为Banach空间,J∈C1(X,)满足:

1)J(0)=0, 存在ρ>0,α>0, 使得J∂Bρ≥α;

2) 存在e∈XBρ, 使得J(e)≤0.

保持好心态听起来像句空话，但在柴松岩眼里，“做人不要自讨苦吃”是最有效的方法。“很多事情，年轻时候根本不是个事，但上岁数以后，扛不住了，就得学会躲，学会选择。要尽量避免情绪的过度波动，不找刺激，比如苦情的电视剧、电视节目基本不看，家长里短、是是非非，离得远远的，不掺和，不劳神。即便是高兴的事，也要把握度，学会适度控制。”

令Γ是X中连接0与e道路的集合, 即

Γ={γ∈C([0,1],X):γ(0)=0,γ(1)=e}.

记

则c≥α, 且J具有(PS)c序列.如果J满足(PS)c条件, 则c是J的临界值.

3 定理1的证明

下面利用山路引理分3步证明方程(3)非平凡解的存在性.

1) 能量泛函J满足(PS)c条件.

令{vn}为(PS)c序列, 取

则wn∈D1,p(N).由函数f的性质(v)可知

从而有‖wn‖≤c‖vn‖.因此

从而可得

表明序列vn在D1,p(N)中强收敛到v.

2) 能量泛函J满足定理2中条件1)和2).

由函数f的性质(vii)、 Hardy-Littlewood-Sobolev不等式和Sobolev嵌入定理可知, 存在正常数c1, 使得

因为p0, 使得当‖v‖=ρ时有J(v)≥α.因此定理2中条件1)成立.

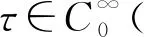
f(tτ(x))≥f(t)τ(x).

从而

利用2q>p和函数f的性质(vi)可推出当t0足够大时,J(t0τ)<α且t0‖τ‖q>ρ.令e=t0τ, 于是定理2中条件2)成立.

3) 方程(3)存在一个非平凡解.

由于J(0)=0, 结合定理2可知, 泛函J存在一个非平凡临界点u且J(u)≥α.于是方程(3)存在一个非平凡的弱解.定理1证毕.