一个参数未知的网格多涡卷超混沌系统的自适应同步

许荣今, 李木子, 岳立娟

(东北师范大学 物理学院, 长春 130024)

由于网格多涡卷混沌系统具有更复杂的拓扑结构和动力学行为, 因此使网格混沌吸引子在信息加密和安全通信中具有广泛的应用前景. Suykens等[1]在蔡氏系统上引入由绝对值函数组成的非线性函数, 构造了第一个单方向多涡卷混沌吸引子. 之后人们提出了应用分段线性函数、 阶跃函数、 正弦函数、 双曲正切函数等非线性函数构造单方向多涡卷混沌系统[2-7], 网格多涡卷混沌吸引子具有更高的复杂特性. 文献[8-11]用不同的非线性函数构造网格多涡卷混沌系统: Yalcin等[8]提出了一个引入阶跃函数构造的网格多涡卷混沌系统; Deng等[9]引入滞回函数构造了网格多涡卷混沌系统; 张朝霞等[10]在蔡氏系统上引入阶跃函数和多项式构造了网格多涡卷混沌系统; Xu等[11]在三维系统中引入由双曲正切函数组成的非线性函数构造了网格多涡卷混沌系统. 目前网格多涡卷系统大部分是混沌的, 但超混沌系统具有更复杂的动力学特性.

混沌同步方法包括广义同步、 滑模同步、 反馈同步、 自适应同步等[12-16]. 其中自适应同步具有鲁棒性强和稳定性高等特点. 在很多实际情况下, 系统参数不能确定, Park[17]提出了参数不确定Rössler系统的自适应同步； 陈士华等[18]在参数辨识方法的基础上, 研究了Rössler超混沌系统自适应同步； 阿布都热合曼·卡的尔等[19]研究了参数未知的统一超混沌系统自适应同步； 黄玮[20]研究了参数未知Lü系统的自适应同步. 由于网格多涡卷混沌系统的构造更复杂, 因此对其同步的研究较少. 本文通过引入双曲正切函数, 构成一个网格多涡卷超混沌系统, 相比于传统的非线性函数, 双曲正切函数作为连续可微函数, 更易分析混沌同步, 并有助于理解神经网络存在的复杂动力学行为. 随着涡卷数的增加, 系统的最大Lyapunov指数和复杂度均增加, 动力学特性变得更复杂. 本文基于Lyapunov指数稳定理论, 对该系统进行了参数未知的自适应同步研究. 数值仿真结果表明, 该方法可较好地实现参数不确定网格多涡卷超混沌系统的同步.

1 网格多涡卷超混沌系统模型及动力学分析

本文构造一个网格多涡卷混沌系统, 系统模型为

(1)

其中x,y,z,w,v为系统的状态变量,a为系统参数,h(x)和f(y)为如下非线性函数：

通过改变h(x)和f(y)中的i和j扩展系统(1)的鞍焦平衡点个数, 进而产生任意连续的涡卷数.式(2)可在x方向产生偶数个涡卷, 式(3)可在x方向产生奇数个涡卷, 式(4)可在y方向产生偶数个涡卷, 式(5)可在y方向产生奇数个涡卷.鞍焦平衡点类型分为“指标1”和“指标2”两种[21], “指标1”鞍焦平衡点用于产生键带, “指标2”鞍焦平衡点用于产生涡卷.当参数a=1,h(x)选取式(2),f(y)选取式(4),i=1,j=1时, 有4×4个“指标2”鞍焦平衡点, 用“·”标出, 系统(1)在x-y平面的鞍焦平衡点分布如图1所示, 由于每个“指标2”鞍焦平衡点对应1个涡卷, 因此网格涡卷的数量是4×4个.

图1 4×4网格多涡卷吸引子的鞍焦平衡点分布Fig.1 Distribution of saddle focal equilibrium points of 4×4 grid multi-scroll attractors

系统(1)的吸引子相图如图2所示.当系统(1)的初值取(0.64,0.06,0,0.1,0),h(x)选取式(2),f(y)选取式(5),i=1,j=1时, 系统(1)产生的吸引子涡卷数为4×3, 如图2(A)所示； 当h(x)选取式(2),f(y)选取式(4),i=1,j=1时, 系统(1)产生的吸引子涡卷数为4×4, 如图2(B)所示； 当h(x)选取式(3),f(y)选取式(4),i=1,j=1时, 系统(1)产生的吸引子涡卷数为5×4, 如图2(C)所示； 当h(x)选取式(2),f(y)选取式(4),i=2,j=2时, 系统(1)产生的吸引子涡卷数为6×6, 如图2(D)所示.当涡卷数不同时, 对应Lyapunov指数列于表1.

图2 系统(1)的吸引子相图Fig.2 Attractor phase diagram of system (1)

表1 不同涡卷数的Lyapunov指数

由表1可见, 随着涡卷数的增加, 系统(1)的Lyapunov指数始终有2个正的, 1个趋近于0, 2个负的, 在不同的涡卷数下, 始终均为超混沌状态.

以4×6网格为例,h(x)选取式(2),f(y)选取(4)式,i=1,j=2, 当参数a改变时, 其状态变量x和y的分岔图如图3所示, Lyapunov指数谱如图4所示.

图3 系统(1)随a变化的分岔图Fig.3 Bifurcation diagram of system (1) with a variation

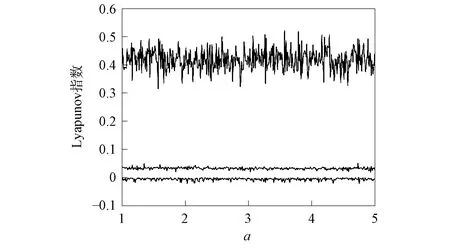
图4 系统(1)随a变化的Lyapunov指数谱Fig.4 Lyapunov exponential spectrum of system (1) with a variation

由图3可见, 在x方向有并行的4条线, 在y方向有并行的6条线, 即系统(1)此时涡卷数为4×6.由图4可见, 当a从1变化到5时, 始终有2个正Lyapunov指数、 1个趋近于0、 2个负的Lyapunov指数(未画出), 系统处于超混沌状态.

为进一步探讨网格多涡卷超混沌系统的复杂性, 用文献[22]中计算复杂度的方法研究系统(1)的复杂度, 计算网格混沌吸引子在x和y方向的复杂度, 结果列于表2.由表2可见, 随着网格涡卷数的增加, 系统在x和y方向的复杂度明显增加, 系统的复杂度越大, 其保密通信的效果越好.

表2 网格多涡卷混沌系统的复杂度

2 参数未知网格多涡卷超混沌系统的自适应同步

系统(1)为驱动系统, 响应系统为

(6)

其中a1为响应系统中需估计的参数,u=(u1,u2,u3,u4,u5)T为控制器.

定义误差为

(7)

则误差系统为

(8)

设计控制器为

(9)

参数自适应律为

(10)

选取Lyapunov函数为

(11)

对V求导可得

选取驱动系统(1)的初值为(5,-3,5,-3,0), 响应系统(6)的初值为(-1,-1,-1,5,2), 取α1=10.9,α2=10.95,α3=10.85,α4=10.8,α5=10.8,η=0.95,ei(i=1,2,3,4,5)随时间t的变化如图5所示.由图5可见, 误差快速趋近于0.参数自适应律ki(i=1,2,3,4,5)收敛曲线如图6所示.由图6可见, 参数ki在较短的时间内趋近于常数.参数a的辨识曲线如图7所示.由图7可见, 参数a在较短的时间内稳定收敛于估计值.

图5 ei(i=1,2,3,4,5)随时间t的变化曲线Fig.5 Change curves of ei(i=1,2,3,4,5) with time t

图6 参数自适应律ki(i=1,2,3,4,5)的控制曲线Fig.6 Control curves of parameter adaptive law ki(i=1,2,3,4,5)

图7 参数a的辨识曲线Fig.7 Identification curve of parameter a

综上, 本文提出了一个网格多涡卷超混沌系统, 该系统仅有一个参数, 通过对系统Lyapunov指数谱的分析表明, 当参数变化范围较大时, 该系统始终处于超混沌状态, 通过Lyapunov指数和复杂度的分析表明, 随着涡卷数的增加, 系统的最大Lyapunov指数和复杂度均增加, 并根据Lyapunov稳定性理论对网格多涡卷超混沌系统进行了参数未知的自适应同步, 仿真结果表明, 该方法在较短的时间内实现了两个系统同步, 且同步效果较好, 可应用于保密通信.