MV-代数的广义导子
王军涛, 肖佳平, 王申桥, 郭静贤, 陈鹏英, 程颂
(西安石油大学理学院应用数学系, 陕西 西安 710065)
1 引言
在经典逻辑推理中, 已知前提所使用的概念和提供的信息都是精确的, 就能保证推得的结果也是准确无误的, 这种精确的, 严格的逻辑推理是人工智能科学及相关研究中普遍采用的方法, 形成了传统计算机的理论基础. 然而传统计算机通常只能按照经典逻辑进行识别, 对模糊概念却无能为力. 为了克服经典逻辑在计算机应用中的不足, 文献[1] 提出了模糊逻辑的概念, 从而使计算机不但可以对模糊概念进行处理, 还可以在信息有限的情况下, 提供精确的答案. 模糊逻辑主要采用代数逻辑的研究方法, 而后者则以逻辑代数为工具来进行研究, 由此可知, 逻辑代数在模糊逻辑的研究中起着十分重要的作用[2-7]. 在模糊逻辑对应的代数系统研究中, MV- 代数是一类最重要的逻辑代数. MV- 代数最初是由文献[8] 提出, 随后不少学者对MV- 代数的性质进行了研究, 得到了一些重要的结论[8-9]. 导子理论来源于分析学, 将它引入代数系统中有助研究代数系统的结构和性质. 一些学者在环和近似环上研究了微分算子的性质[10-11]. 文献[12]将环上的微分算子理论引用到BCI- 代数中, 得到了一些重要的结果. 文献[13] 将导子的理论应用到格上, 并利用保序导子刻画了模格、分配格的结构. 文献[14] 尝试研究了MV- 代数上的(⊙,⊕) 导子, 得到了基本的结论; 文献[15] 深入研究了MV- 代数上的(⊙,⊕)- 导子和(⊖,⊙)- 导子, 并刻画了保序(⊙,⊕)- 导子. 文献[16] 在MV- 代数中引入了(⊙,⊕)- 导子, 讨论了这类导子与MV- 代数上其它导子之间的关系, 得到了一些重要的结论. 2014 年, 辛小龙教授通过利用MV- 代数上的自同态映射将文献[17] 中的两类导子进行了推广, 得到了MV- 代数的f和g导子, 讨论了两者之间的联系, 研究了其不动点之集与理想之间的关系.
本文借助于MV- 代数上的自同态, 引入并研究了其上的广义(⊙,⊕)- 导子, 给出其等价刻画, 并利用广义(⊙,⊕)- 导子得到了MV- 代数成为Boole 代数的等价条件, 推广了现有文献中的相关结论, 进一步刻画了MV- 代数的结构.
2 预备知识
定义2.1一个MV-代数是(2,1,0)型代数(A,⊕,∗,0)满足如下公理:∀x,y,z ∈A,
(MV1)x ⊕(y ⊕z)=(x ⊕y)⊕z;
(MV2)x ⊕y=y ⊕x;
(MV3)x ⊕0=x;
(MV4)x∗∗=x;
(MV5)x ⊕0∗=0∗;
(MV6) (x∗⊕y)∗⊕y=(y∗⊕x)∗⊕x.
在MV- 代数A中记0∗=1 并定义二元运算⊙,∧,∨,→,⊖如下:
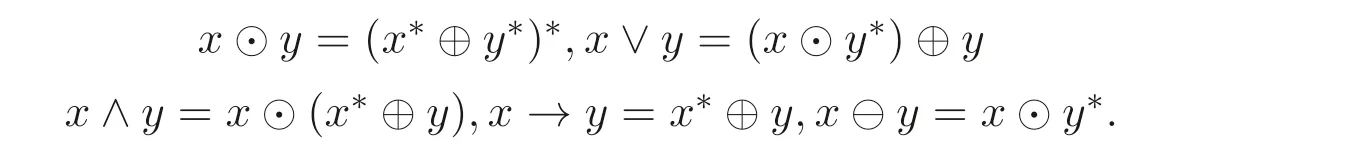
显然(A,⊙,1) 是一个可换含幺半群, 且(A,∧,∨,0,1) 是一个有界分配格. 在MV-代数中定义偏序关系≤为x ≤y当且仅当x ∧y=x. 定义x∗=x →0. 若A中任意两个元素都存在偏序关系, 则称A是线序的. 此外, 集合
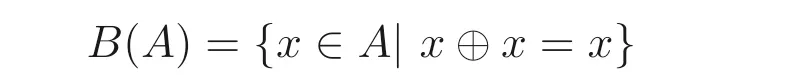
为A的布尔中心, 则(B(A),⊕,∗,0) 是一个布尔代数.
命题2.1设A是MV- 代数, 则下列结论成立:∀x,y,z ∈A,
(1)x ⊕x∗=1,x ⊙x∗=0;
(2)x ≤y当且仅当x ⊙y∗=x ⊖y=0 当且仅当x →y=1;
(3) 若x ≤y, 则y →z ≤x →z,z →x ≤z →y,y∗≤x∗;
(4)x ⊙y ≤x ∧y ≤x,y ≤x ∨y ≤x ⊕y;
(5)x ∨y=(y →x)→x=(x →y)→y;
(6)x ⊕y=y当且仅当x ⊙y=x;
(7) (x ⊖y)⊕y=x ∨y,x ⊖(x ⊖y)=x ∧y;
(8) (x ⊖z)⊖y=(x ⊖y)⊖z;
(9)x ∧(y ⊕z)=(x ⊕z)∧(x ⊕y).
定理2.1设A是MV- 代数, 下列结论等价:
(1)x ∈B(A);
(2)x ⊕y=x ∨y,∀y ∈A;
(3)x ⊙y=x ∧y,∀y ∈A.
定义2.2设A是MV- 代数,I是A的子集, 满足以下条件:∀x,y ∈A,
(1) 0∈I;
(2) 若x ∈I,y ∈A, 且x ≤y, 则x ∈I;
(3) 若x,y ∈I, 则x ∨y ∈I, 则称I是A的理想.
定义2.3设A是MV- 代数,F是A的子集, 若F满足以下条件:∀x,y ∈A,
(1) 1∈F;
(2) 若x ∈F,y ∈A, 且x ≤y, 则y ∈F;
(3) 若x,y ∈F, 则x ∧y ∈F, 则称F是A的格滤子;
(4) 若∀x,y ∈F,x ∨y ∈F, 则x ∈F或y ∈F, 则称F是A的格素滤子.∀a ∈A,(a] 表示由a生成的滤子, 称(a] 为主滤子, 容易验证(a]={x ∈A|x ≥a}.
定义2.4设P是偏序集,P上的二元运算⊕和⊖互为余伴随, 若以下条件成立:
(1)⊕:P×P →P是单调递增的;
(2)⊖:P×P →P是关于第一变量不减, 关于第二变量不增;
(3)c ≤a ⊕b当且仅当c ⊖b ≤a.
定义2.5设M,N是MV- 代数,f:M →N是映射, 若f满足以下条件:
(1)f(0)=0;
(2)f(x ⊕y)=f(x)⊕f(y);
(3)f(x∗)=(f(x))∗,∀x,y ∈A, 则称f是MV- 代数的同态.
定义2.6设A是一个MV- 代数,d:A →A是映射. 若存在A的自同态f使得d满足:∀x,y ∈A,d(x ⊙y)=(d(x)⊙f(y))⊕(f(x)⊙d(y)), 则d是A上的f导子.
定义2.7设A是一个MV- 代数,d:A →A是映射. 若存在A的自同态g使得d满足:∀x,y ∈A,d(x ⊖y)=(d(x)⊖g(y))⊕(g(x)⊖d(y)), 则d是A上的g导子.
定义2.8设A是一个MV- 代数,d:A →A是映射. 若d满足:∀x,y ∈A,
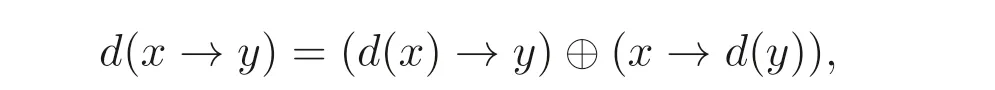
则d是A上的(→,⊕) 导子.
3 MV- 代数的广义(→,⊕)- 导子
本文引入了MV- 代数的广义(→,⊕)- 导子, 并研究它的一些代数性质.
定义3.1设A是一个MV- 代数,d:A →A是映射,f:A →A是A上的自同态. 若d满足:∀x,y ∈A,d(x →y)=(d(x)→f(y))⊕(f(x)→d(y)), 则称d是A的广义(→,⊕)- 导子.
例3.1设A是一个MV- 代数, 定义映射d:A →A为d(x) = 1,∀x ∈A,f:A →A是A上的自同态, 由于
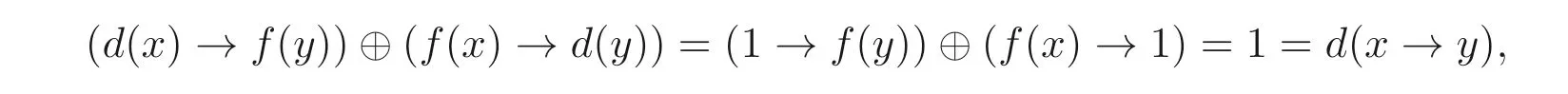
显然,d是A的广义(→,⊕)- 导子, 称d为平凡广义(→,⊕)- 导子.
例3.2设A={0,a,b,1}, 其中0≤a ≤b ≤1. 定义二元运算⊕和∗如下:
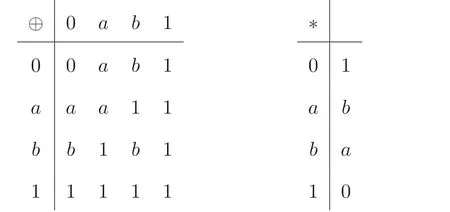
则(A,⊕,∗,0,1) 是MV- 代数. 分别定义映射d:A →A, 映射f:A →A为
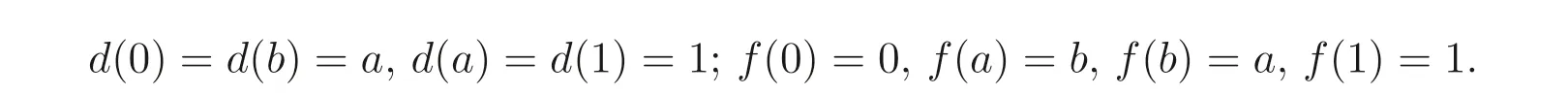
容易验证d是A的广义(→,⊕)- 导子, 然而
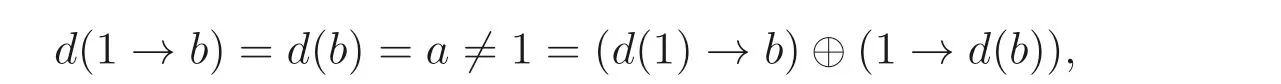
因此,d不是A的(→,⊕)- 导子.
注3.1例3.2 中的(→,⊕)- 导子d, 其定义中d(0)̸= 0, 因此d不是文献[17] 中的f,g导子.
命题3.1设d是MV- 代数A的广义(→,⊕)- 导子, 则下列结论成立:∀x,y ∈A,
(1)d(1)=1;
(2)d(x)=f(x)⊕d(x);
(3)f(x)≤d(x);
(4)x ≤y蕴涵d(x)≤d(y);
(5)d(x)→f(y)≤f(x)→d(y);
(6)d(x)→d(y)≤d(x →y).
证明(1)d(1)=d(1→1)=(d(1)→f(1))⊕(f(1)→d(1))=1.
(2)d(x)=d(1→x)=(d(1)→f(x))⊕(f(1)→d(x))=f(x)⊕d(x).
(3) 由(2) 可知f(x)≤f(x)⊕d(x)=d(x).
(4) 若x ≤y, 则y=x ∨y, 因此
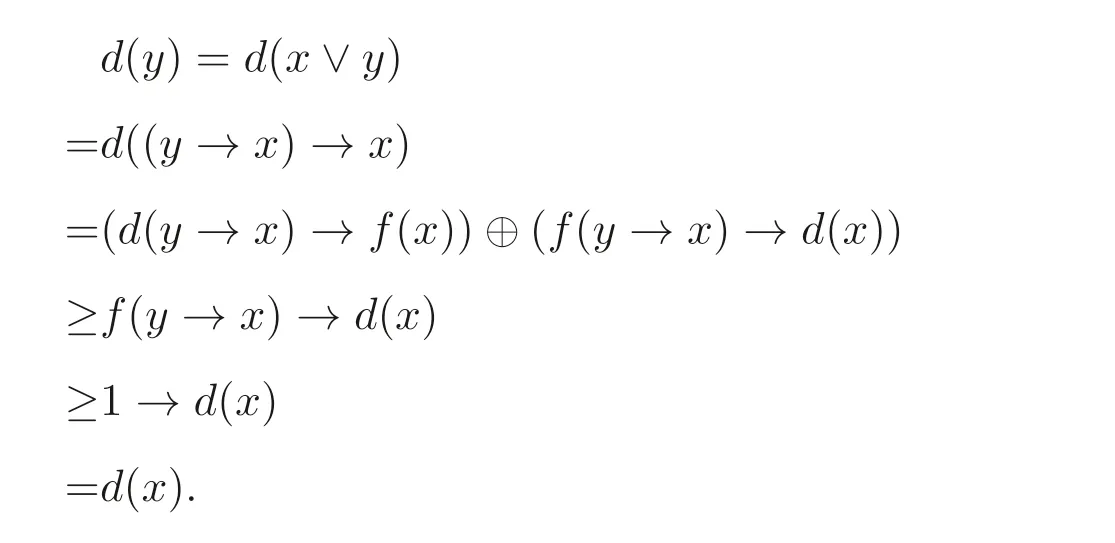
(5) 由命题2.1(3) 和命题3.1(3) 可得.
(6) 由定义3.1, 命题2.1(3) 和命题3.1(3) 可得
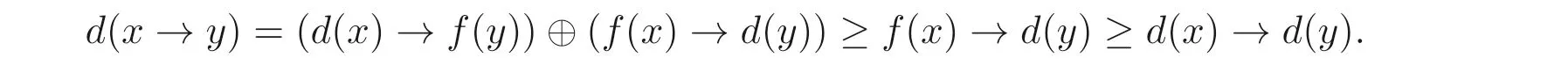
定义3.2设d是MV- 代数A的广义(→,⊕)- 导子. 若d(0)=0, 则称d是MV-代数A的正则广义(→,⊕)- 导子.
例3.3设A是例3.2 中的MV- 代数, 分别定义映射d:A →A, 映射f:A →A为
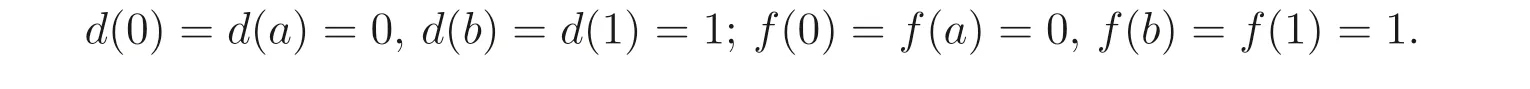
则容易验证d是A的正则广义(→,⊕)- 导子.
命题3.2设d是MV- 代数A的正则广义(→,⊕)- 导子, 则下列结论成立:∀x,y ∈A,
(1) (d(x))∗≤d(x∗);
(2)d(x ⊕y)≤d(x)⊕d(y);
(3)d(x)⊖d(y)≤d(x ⊖y).
证明(1) 根据命题2.1(6) 和d(0)=0 可得.
(2) 由定义3.1 和命题3.2(1) 知
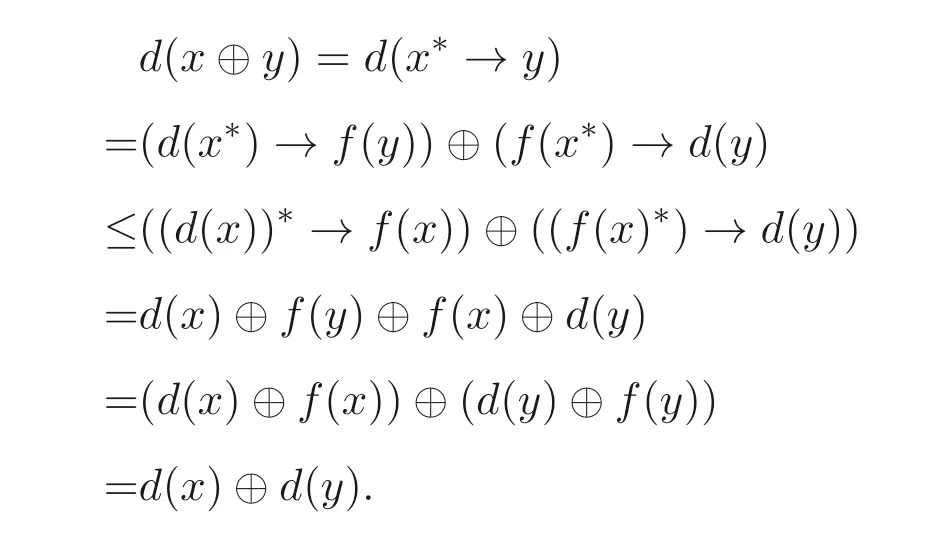
(3) 由命题2.1(8), 命题3.1(4) 和命题3.2(2) 可知
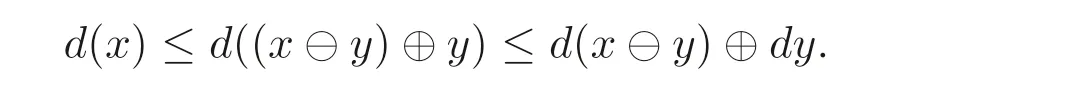
下面讨论MV-代数A上布尔中心上的广义(→,⊕)-导子的一些性质,并给出MV-代数A上布尔中心上的广义(→,⊕)- 导子的等价刻画.
命题3.3设d是MV- 代数A的广义(→,⊕)- 导子, 则下列结论成立:∀x,y ∈B(A),
(1)d(B(A))⊆B(A);
(2)d(x →y)=(d(x)→f(y))∨(f(x)→d(y));
(3)d(x →y)=f(x)→d(y);
(4)d(x ∨y)≤d(x)∨d(y);
(5) 若d(0)=0, 则d(x∗)=f(x∗);
(6) 若d(0)=0, 则d(x ∧y)=f(x)∧f(y).
证明(1) 设x ∈B(A), 由于f是自同态, 则f(x)∈B(A), 进而由命题2.1(2) 和定理2.1 可知
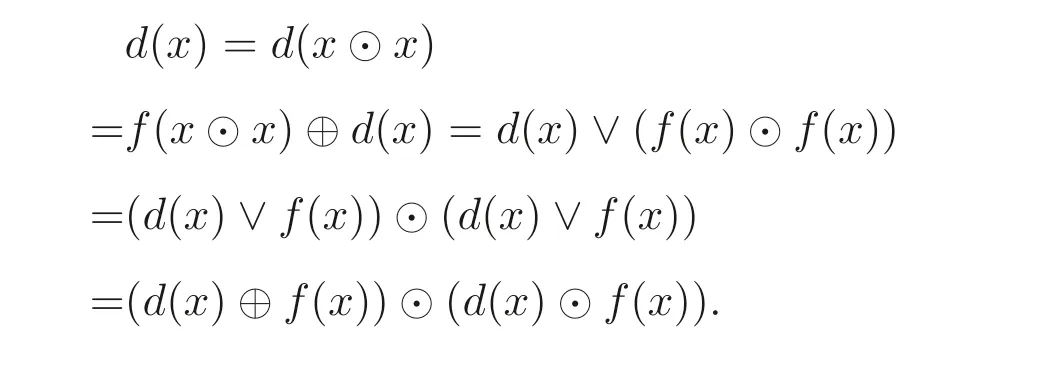
因此
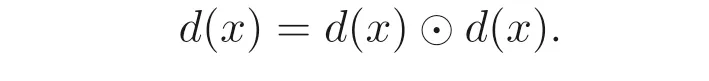
(2) 设x,y ∈B(A), 由(1) 和定理2.1(2) 可知
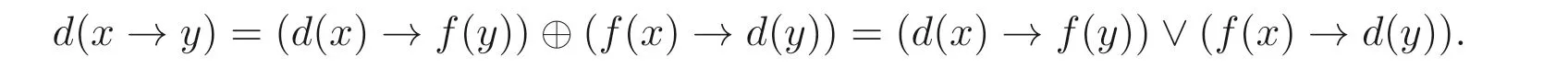
(3) 由(2) 和命题2.1(5) 可得d(x →y)=f(x)→d(y).
(4) 由命题2.1(2) 可得d(x ∨y)=d(x ⊕y)≤d(x)⊕d(y)=d(x)∨d(y).
(5) 由(3) 和d(0)=0 可知d(x∗)=d(x →0)=f(x)→d(0)=(f(x))∗=f(x∗).
(6) 由(5) 可知
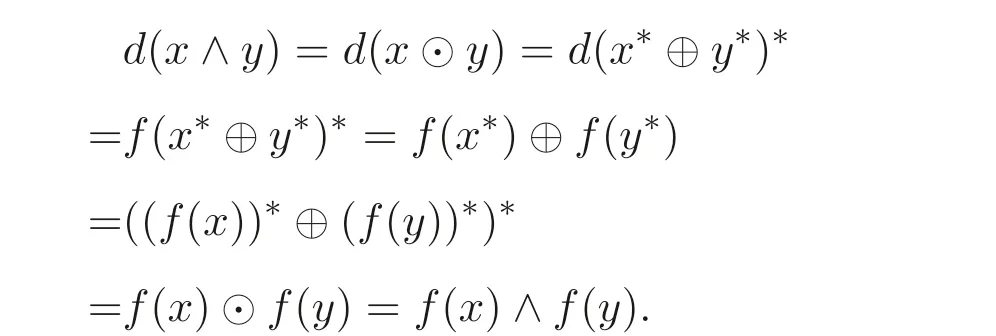
推论3.1设d是MV- 代数A上的一个映射, 则以下结论等价:
(1)d是B(A) 上的广义(→,⊕)- 导子;
(2)d(x →y)=f(x)→d(y),∀x,y ∈B(A).
证明(1)⇒(2) 由命题2.1(5) 和命题2.3(2) 可得.
(2)⇒(1) 假设d是B(A) 上的映射且满足∀x,y ∈B(A),d(x →y) =f(x)→d(y),则
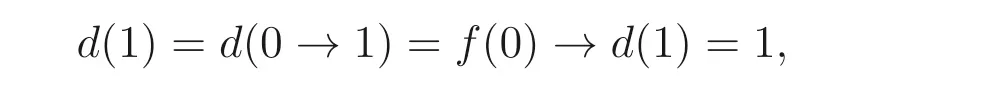
又
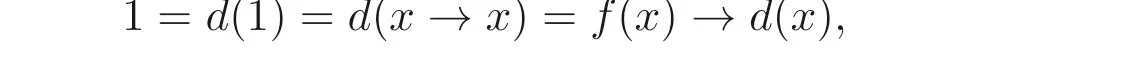
因此∀x ∈B(A),f(x)≤d(x), 进而由命题2.1(3) 可知d(x)→f(y)≤f(x)→d(y). 因此,
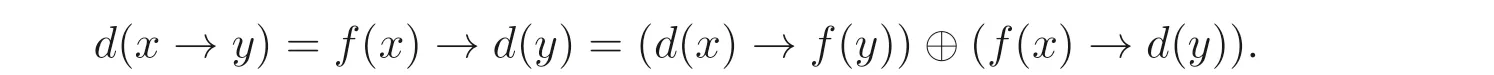
设A是MV-代数,d:A →A是一个映射,f:A →A是A上的一个自同态. 定义
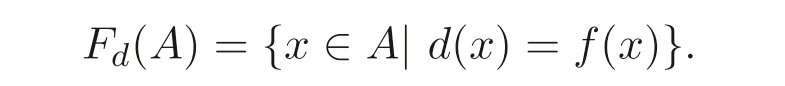
命题3.4设d是MV- 代数A的广义(→,⊕)- 导子, 则Fd(A)⊆B(A).
证明设x ∈Fd(A), 由命题2.1(2) 可知d(x)=f(x)⊕d(x), 则
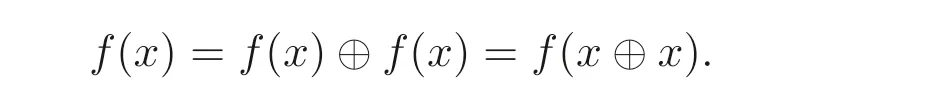
又由于f是自同态, 所以x ⊕x=x, 因此x ∈B(A).
注3.2命题3.3 的逆命题一般不成立. 设A是例3.2 中的MV-代数, 分别定义A上的映射d和单同态f为∀x ∈A,d(x) = 0;f(0) = 0,f(1) = 1,f(a) =b,f(b) =a.则易验证Fd={0}⊆{0,a,b,1}⊆B(A), 但是d不是A上的广义(→,⊕)- 导子. 因为

定理3.1设A是MV- 代数,f:A →A是A上的单同态, 则以下结论等价:
(1)A是Boole 代数;
(2) 映射d=f是广义(→,⊕)- 导子.
证明(1)⇒(2) 假设A是Boole 代数且映射d=f, 则d(x →y) =f(x)→d(y).由推论3.1 可知,d是Boole 代数A的广义(→,⊕)- 导子.
(2)⇒(1) 假设映射d=f是A上的广义(→,⊕)- 导子, 由命题3.4 可知
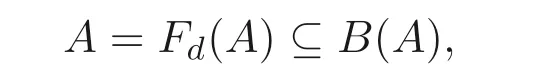
因此A是Boole 代数.
由定理3.3 可知, 若A是Boole 代数,f:A →A是A上的单同态, 则映射d=f是A上的广义(→,⊕)- 导子. 下面这个定理给出了Boole 代数上的映射d=f时广义(→,⊕)- 导子的等价刻画.
定理3.2设d是Boole 代数A上的广义(→,⊕)- 导子,f:A →A是A上的单同态, 则以下结论等价:
(1) 映射d=f;
(2)∀x,y ∈A,f(x)→d(y)=d(x)→f(y).
证明(1)⇒(2) 显然.
(2)⇒(1) 假设∀x,y ∈A,f(x)→d(y)=d(x)→f(y). 由推论3.1 可知
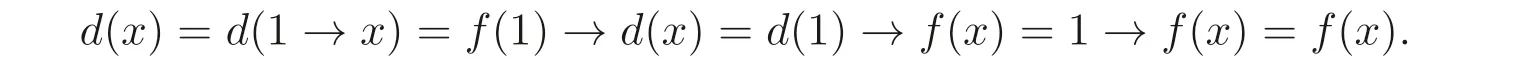
因此映射d=f.
命题3.5设A是MV- 代数,f:A →A是A上的自同态,a ∈A,
(1) 定义da:A →A为∀x ∈A,da(x) =a ⊕f(x). 若da(A)⊆B(A), 则da是A的广义(→,⊕)- 导子.
(2) 若f满足f(a)=a, 定义
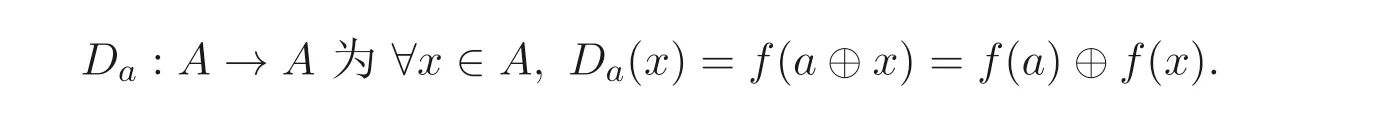
若Da(A)⊆B(A), 则Da是A的广义(→,⊕)- 导子.
证明由定义2.1, 命题2.2 知,∀x,y ∈A,
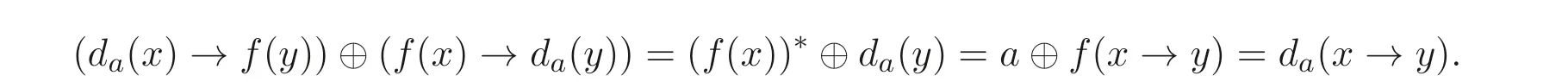
由定义2.8 知,da是A的广义(→,⊕)- 导子.
注3.3由于da是MV- 代数A的布尔中心上的广义(→,⊕)- 导子, 称da是MV-代数A的中心主微分; 由于Da是MV- 代数A的布尔中心上的强广义(→,⊕)- 导子,称Da是MV- 代数A的强主中心广义导子.
命题3.6设A是MV- 代数,f:A →A是A上的自同态, 则存在A上的自映射
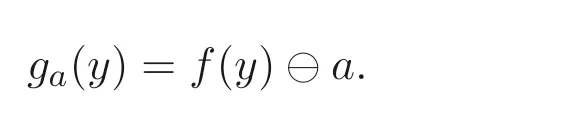
使得(da,ga) 是A上的一对余伴随.
证明显然⊕是单调不减的,⊖是关于第一变量不增, 关于第二变量不减并且∀x,y,a ∈A,
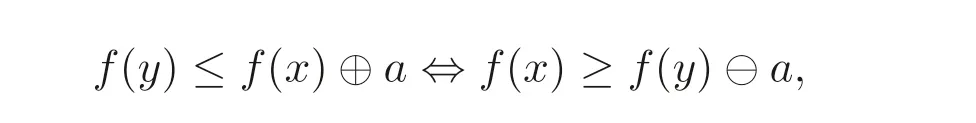
由定义2.4 可知(da,ga) 是A上的一对余伴随.
命题3.7设A是MV- 代数. 如果ga(A)⊆B(A), 则ga是g导子.
证明设ga(A)⊆B(A). 设∀x,y ∈A,g:A →A是A的自同态, 由命题2.1(8) 知
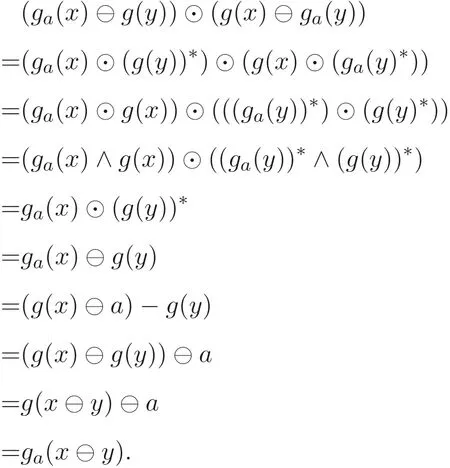
由定义2.7 可知ga是MV- 代数的g导子.
命题3.8设A是MV- 代数. 如果ga(A)⊆B(A), 则ga是f导子.
证明设ga(A)⊆B(A). 设∀x,y ∈A,g:A →A是A上的自同态,
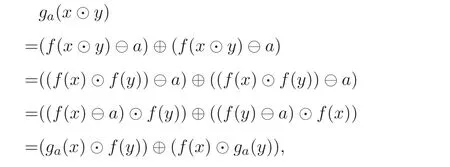
由定义2.6 可知ga是f导子.
引理3.1设d是MV- 代数A的f导子, 则下列结论等价:
(1)d是保序的;
(2)∀x ∈A,d(x)=f(x)⊙d(1).
命题3.9(1) 设A是MV- 代数,d是A上的保序f导子. 若存在A上的自映射f满足f(A)⊆B(A), 且(d,f) 是A上的一对余伴随对, 则f是A上广义(→,⊕)-导子.
证明由命题3.5- 命题3.6, 命题3.8 可证.
(2) 设A是Boole 代数,g是A上的g导子. 若存在A上的自映射f满足(g,f)是A上的余伴随对, 则f是A上广义(→,⊕)- 导子.
证明由命题3.5- 命题3.7 可证.
定理3.3设d是MV- 代数A上的正则广义(→,⊕)- 导子, 则以下结论等价:
(1)A是Boole 代数;
(2)Fd(A) 是A的格滤子.
证明(1)⇒(2) 假设A是Boole 代数且d是A上的正则广义(→,⊕)- 导子, 由于f(1)=d(1)=1, 故1∈Fd(A). 若x,y ∈Fd(A), 则d(x)=f(x),d(y)=f(y), 由命题2.1(6) 可得d(x ∧y)=d(x)∧d(y)=f(x)∧f(y)=f(x ∧y), 则x ∧y ∈Fd(A). 下面证明Fd(A) 是A的上集. 若x ∈Fd(A),y ∈A且x ≤y, 则
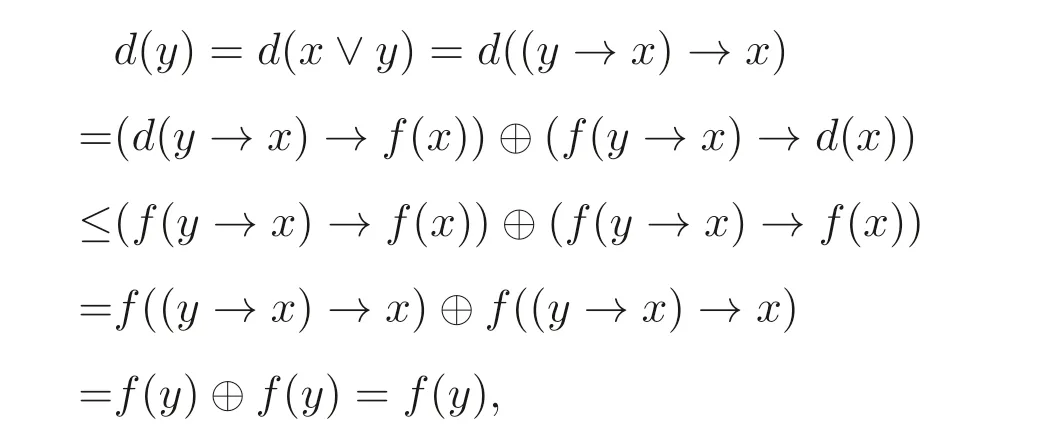
从而d(y)≤f(y). 另一方面, 由命题2.1(3)知f(y)≤d(y), 故f(y)=d(y). 因此Fd(A)是A的格滤子.
(2)⇒(1) 假设Fd(A) 是A的格滤子, 由正则广义(→,⊕)- 导子的定义可知
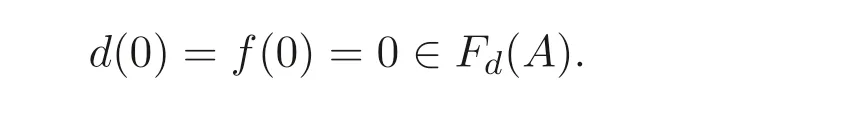
从而Fd(A)=A. 由命题3.4 知,A ⊆B(A), 故A是Boole 代数.
定理3.4设d是A的广义(→,⊕)- 导子,f:A →A是A的保序单同态, 则以下结论等价:
(1)A是Boole 代数;
(2) 每一个强主中心广义导子Da满足FDa(A)=(a].
证明(1)⇒(2) 假设A是Boole 代数, 则∀x ∈A,x ⊕x=x成立. 由于
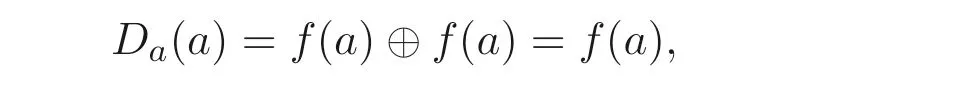
则a ∈FDa(A). 根据定理3.3 得Fd(A) 是A的上集, 因此对∀a ≤x, 有x ∈FDa(A),从而(a]⊆FDa(A).
另一方面, 设x ⊆FDa(A), 则Da(x)=f(x)=f(a)⊕f(x)≥f(a), 由于f是保序的, 则有x ≥a. 这就证明了x ∈(a]. 因此FDa(A)=(a].
(2)⇒(1) 由(2) 知∀a ∈A,FDa(A) = (a]. 由于a ∈(a], 则a ∈FDa(A), 从而有f(a)⊕f(a) =Da(a) =f(a),∀a ∈A成立. 由于f是保序单同态, 则a ⊕a=a,∀a ∈A成立, 即A是一个Boole 代数.
4 结束语
利用MV- 代数的自同态, 将MV- 代数的(→,⊕)- 导子进行了推广, 引入了广义(→,⊕)- 导子, 研究了它们的性质. 此外, 定义并研究了正则广义(→,⊕)- 导子, 并讨论了MV- 代数的布尔中心上的广义(→,⊕)- 导子的一些性质. 最后, 利用广义(→,⊕)-导子给出了MV- 代数成为Boole 代数的等价刻画.

