有限域上一类方程解数的注记
徐碧云, 姜坤, 曹炜
(宁波大学数学与统计学院, 浙江 宁波 315211)
1 引言
Markoff-Hurwitz 类型的方程是指如下形式的丢番图方程
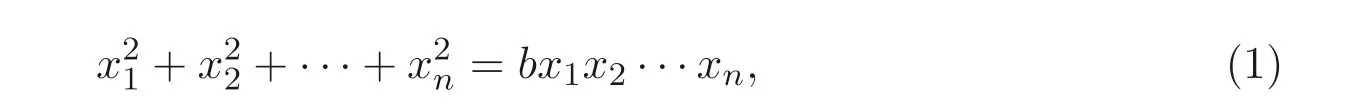
其中n,b均为正整数. 由于它与丢番图逼近理论的紧密联系, 文献[1] 首先研究了它在n=3,b=3 情形时的解数公式; 文献[2] 考察了它的一般形式, 这是此类方程命名的由来.
设Fq是一个特征为p且含有q个元素的有限域, 其中q=pr,r ≥1,p是一个奇素数, F∗q= Fq{0}. 对于多项式f ∈Fq[x1,x2,··· ,xn], 用Nq(f) 表示方程f(x1,x2,··· ,xn)=0 在Fq中的解数. 寻找Nq(f) 的具体表达式是有限域中的一个重要课题. 一般来说, 给出Nq(f) 的具体表达式是比较困难的, 所以需要限制一些特殊条件(参见文献[3-10]).
文献[3] 研究了有限域Fq上的Markoff-Hurwitz 类型的方程
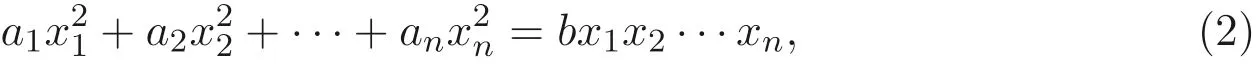
其中a1,··· ,an,b ∈F∗q, 文献[3] 给出了当n=3 和n=4 时在某些特殊情况下的具体解数公式, 并提出了寻找此类方程解数公式的问题.
文献[4] 推广了文献[3] 的上述结果, 得到了n ≥5 时, 其在某些特殊情况下的具体解数公式; 文献[5] 研究了如下广义的Markoff-Hurwitz 类型方程
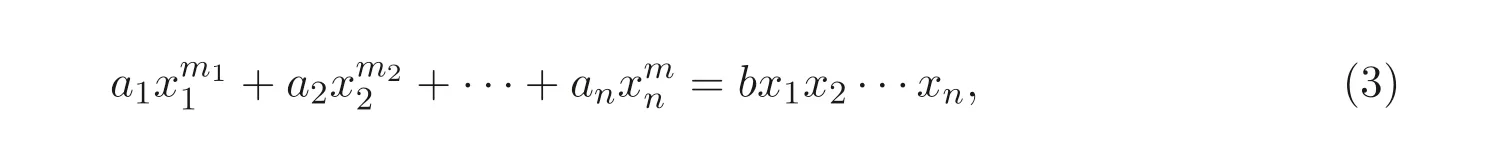
其中ai,b ∈F∗q,mi(i=1,2,··· ,n) 为正整数, 利用指数和的工具, 在文献[6] 研究成果的基础上给出了它在某些限制条件下的解数公式.
文献[7] 研究了广义的Markoff-Hurwitz 类型方程
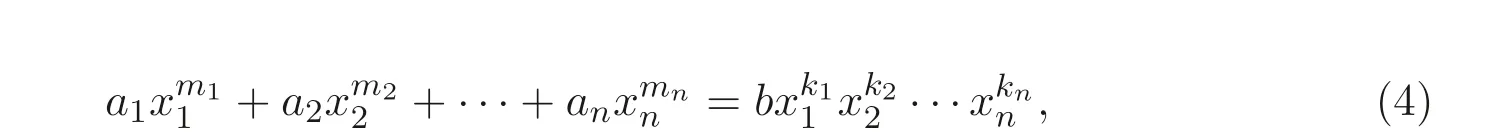
其中ai,b ∈F∗q,mi,ki,i= 1,2,··· ,n,n ≥2 为正整数, 利用剩余类环Z/(q −1)Z 上增广次数矩阵的Smith 标准型给出了其在特殊条件下的解数公式, 推广并简化了文献[5]的相关结果.
文献[9] 考虑了更为广义的Markoff-Hurwitz 类型方程
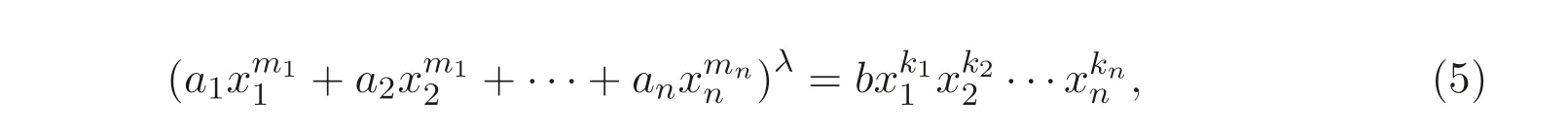
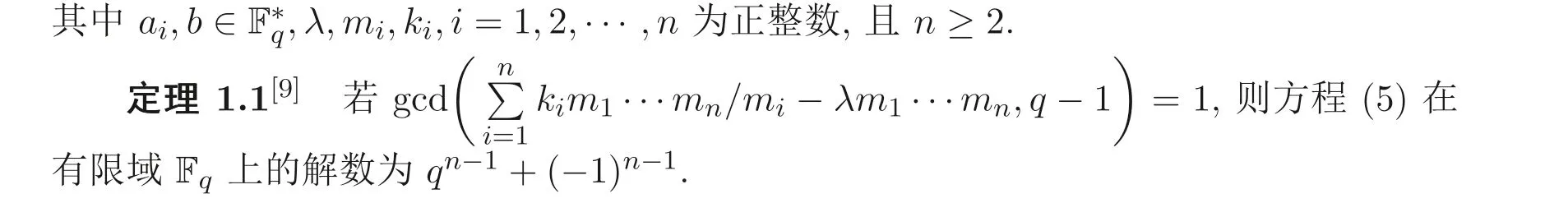
本文将给出定理1.1 的另一种组合证明方法, 并进一步研究如下广义Markoff-Hurwitz 类型方程的解数问题:
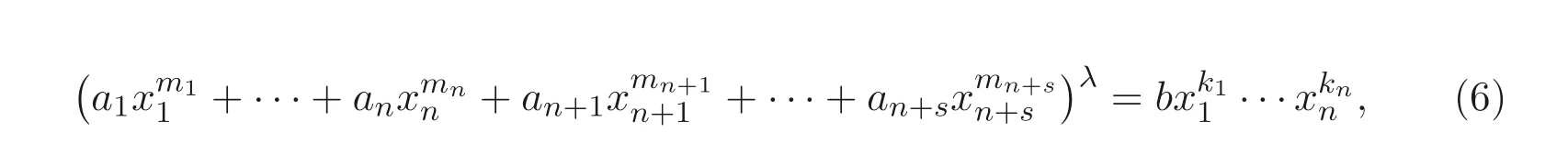
其中ai,b ∈F∗q,λ,mi,kj,i=1,2,··· ,n+s,j=1,2,··· ,n, 且n ≥2,s ≥0 均为整数.
本文的结构安排如下: 在第二节, 介绍一些预备知识; 在第三节, 给出定理1.1 的另一种组合证明; 方程(6) 的解数公式及推论和例子在第四节中给出.
2 预备知识
设f(X) 是Fq上的n元多项式, 记为

对一个给定的向量l= (l1,l2,··· ,lm)∈Ωm, 定义σ(l) 为向量l中非零元的个数.记(v1,v2,··· ,vm)T=l1˜D1+l2˜D2+···+lm˜Dm, 定义s(l) 为(v1,v2,··· ,vm)T中非零元的个数.
设ξp是p次复本原单位根,χ是乘法群F∗q上的Teichm¨uller 特征, 即对任一a ∈F∗q, χ(a) 是q −1 次复本原单位根, 满足χ(a)(modp) =a. 定义Fq上的(q −2) 个高斯和为
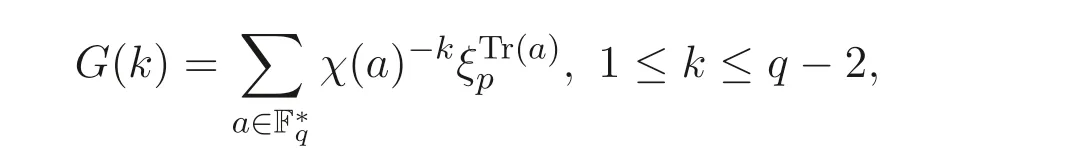

为Fq上的二次高斯和.
引理2.1[12]对q=pr, 有
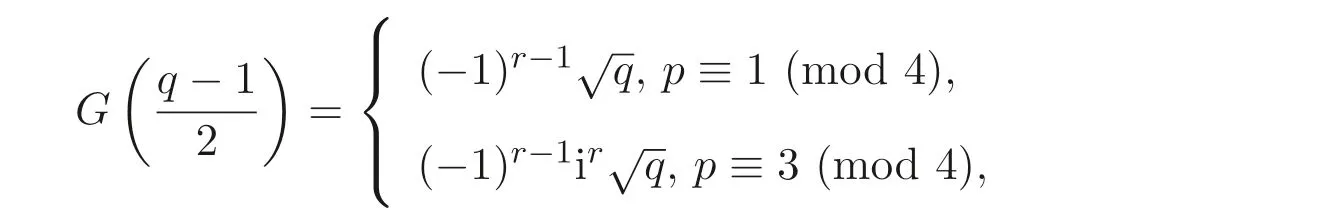
其中i 是虚数单位.
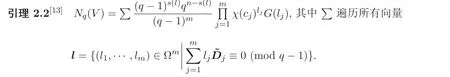
3 定理1.1 的证明
设代数簇V由下列方程组确定:

令(v1,··· ,vn+3)T=˜D(l1,··· ,ln+3)T满足(v1,··· ,vn+3)T≡0 (modq −1), 即

由于条件
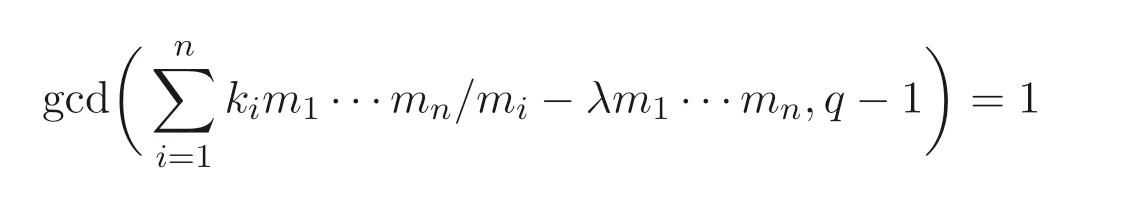
等价于V的增广次数矩阵˜D在剩余类环Z/(q −1)Z 中可逆, 因此由Cramer 法则, 同余方程组˜Dl ≡0(modq −1)只有零解,即(l1,l2,··· ,ln+3)≡(0,0,··· ,0)(modq −1),注意这里l ∈Ωn+3,Ω={0,q −1}.
下面根据(7) 式对σ(l) 和s(l) 的具体情形进行分类讨论.
当σ(l) = 0 时, 即(l1,··· ,ln+3) = (0,··· ,0), 有(v1,··· ,vn+3) = (0,··· ,0),故s(l)=0.
当σ(l)=1 时, 即l1,··· ,ln+3中有1 个不为0, 分两种情形讨论:
(i) 若从l1,··· ,ln+2中任选1 个不为0, 则s(l)=2;
(ii) 若ln+3̸=0 , 则s(l)=n+1.
当σ(l)=2 时, 即l1,··· ,ln+3中有2 个不为0, 分三种情形讨论:

当3≤σ(l)≤n+1 时, 即l1,··· ,ln+3中有σ(l) 个不为0, 分三种情形讨论:

当σ(l)=n+2 或σ(l)=n+3 时,s(l)=n+3.
对上述情形进行合并归纳, 结果见表1.

表1 σ(l), s(l) 及对应个数
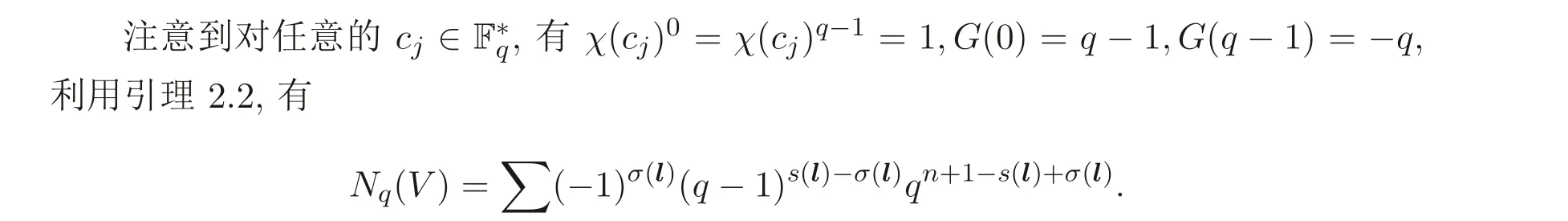
其中∑遍历所有向量l= (l1,··· ,ln+3)∈Ωn+3, 且满足˜DlT≡0 (modq −1). 由此可得
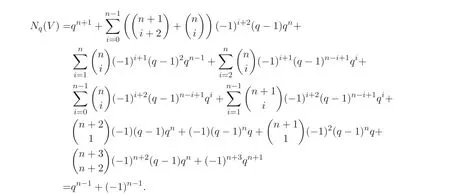
4 推广的Markoff-Hurwitz 方程
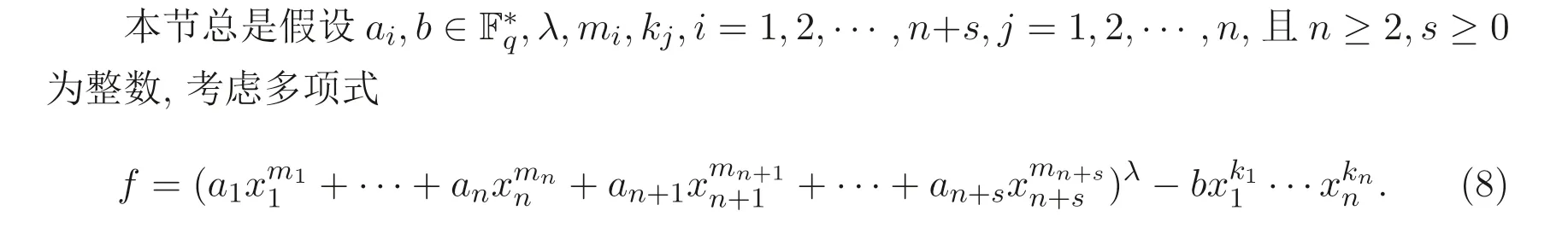
设代数簇V′由下列方程组确定
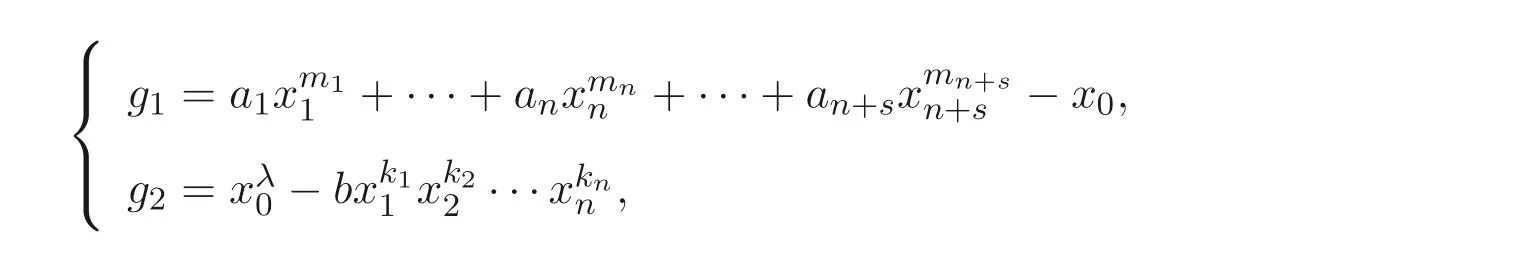
有Nq(f)=Nq(V′).
因此只需要计算Nq(V′). 设V′的增广次数矩阵为˜DV′= (˜D1,˜D2,··· ,˜Dm). 注意到确定V′的多项式组中有n+s+1 个变量. 因此, 由引理2.2 可得

(ii) 当p ≡3 (mod 4) 时,
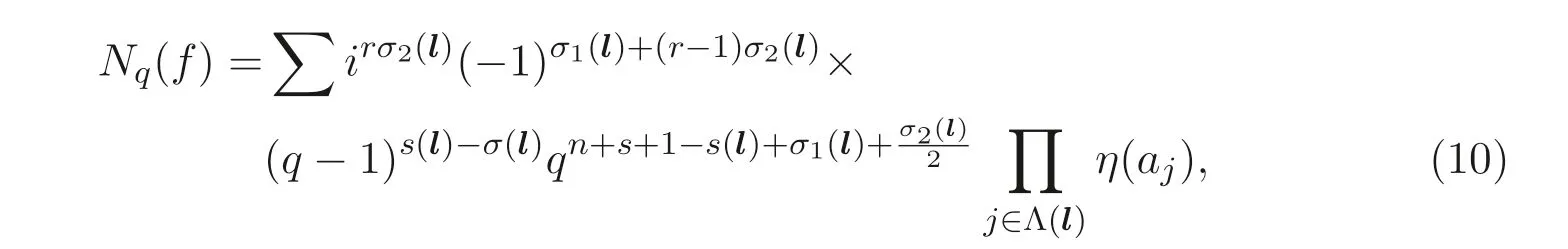

其中(9) 式-(10) 式中的∑遍历所有向量l=(l1,l2,··· ,lm)∈Ωm, 这里其中∑遍历所有向量l=(l1,··· ,ln+3)∈Ωn+3, 且满足˜DV′lT≡0 (modq −1). 利用引理2.1 即可得证. 由Nq(f)=Nq(V′) 可得结论.
推论4.1若gcd(N,q −1)=1, 则
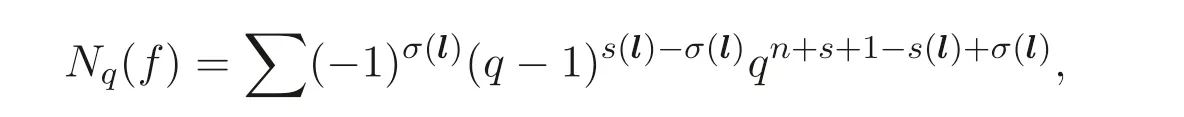
其中∑遍历所有向量l=(l1,l2,··· ,ln+s+3), 使得˜DV′lT≡0 (modq −1).
证明若gcd(N,q −1)=1, 则Ω={0,q −1}, 即σ2(l)=0,Λ(l)=∅,σ1(l)=σ(l),由定理4.1 即可得证.
推论4.2若det(N,q −1)=1 且s=0, 则
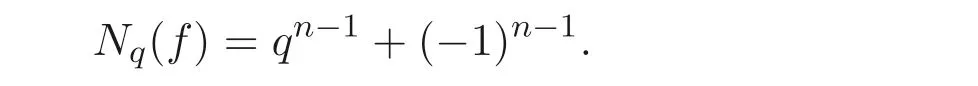
证明由推论4.1 有Nq(f)=∑(−1)σ(l)(q −1)s(l)−σ(l)qn+1−s(l)+σ(l), 其中∑遍历所有向量l=(l1,··· ,ln+3)∈Ωn+3, 且满足˜DV′lT≡0 (modq −1). 再由定理1.1 的证明过程即可得证.
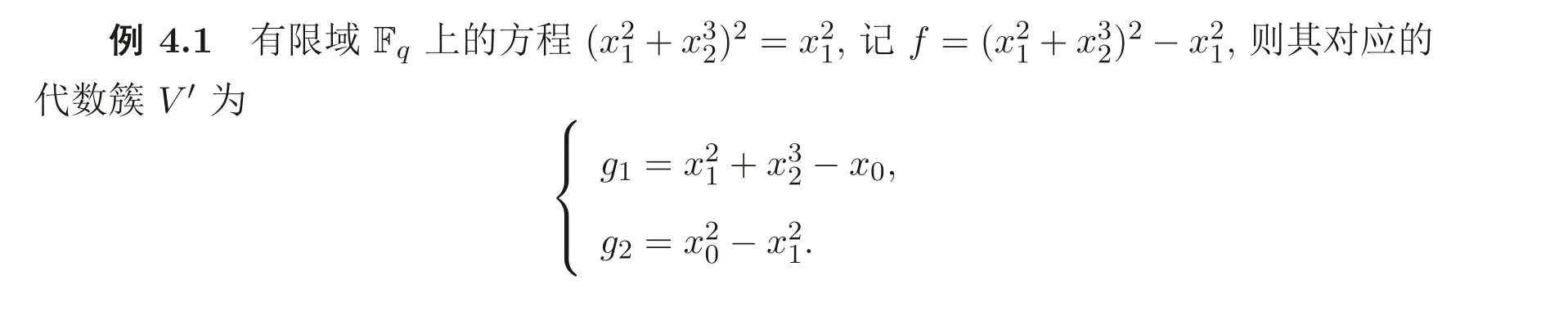
因此V′的增广次数矩阵为
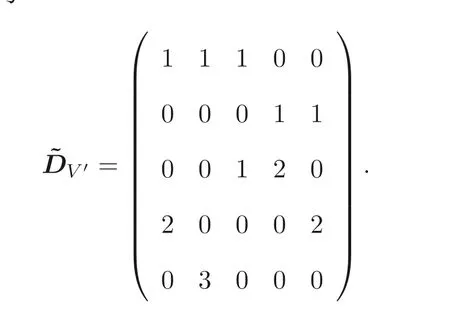
易得, det(˜DV′)=−6, 即N=6.
在剩余类环Z/(q −1)Z 中解同余方程组˜DV′lT≡0 (modq −1), 对满足条件gcd(N,q −1)| 2 的q来说,l的解共有40 种情形. 以q= 3 为例, 每种情形下的σ1(l),σ2(l) 和s(l) 的值列表如表2.
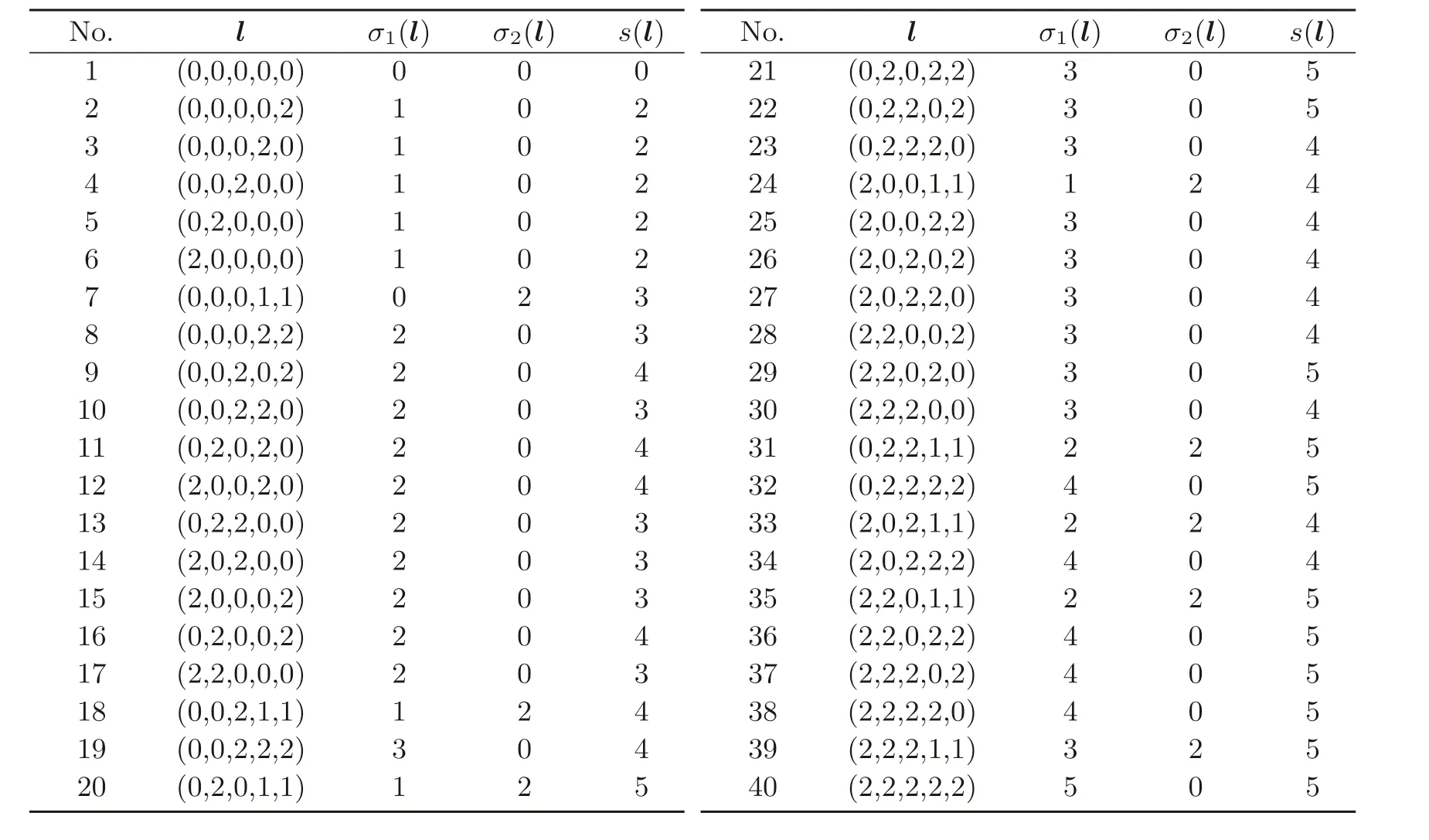
表2 l 及其对应的σ1(l),σ2(l) 和s(l) 的值
由定理4.1 得Nq(f)=5. 对于q=5, 显然也满足条件gcd(N,q −1)| 2, 可用类似方法, 由定理4.1 得Nq(f)=9. 以上结果均与用Matlab 验算的方程实际解数一致.

