用由易入难的数学问题引领学生思维发展

沈庆华

[摘  要] 任何事物的发展都需要过程，思维的培养亦是如此，教学中切勿急于求成，一蹴而就，而应由易入难逐层渗透，让思维螺旋上升. 文章以“同旁内角”的教学为例，运用类比、归纳等数学思想方法，加强对概念内涵和外延的学习，以期培养学生的发散思维、创新思维.

[关键词] 过程;创新思维;全面发展

笔者以“图中有几组同旁内角”为思维发展的主线，采用数形结合的方式让学生经历了由易到难、由特殊到一般的过程，进而培养学生的数学学习能力.

观察特征，巩固概念

众所周知，数学概念学习是数学学习的关键一环，在数学学习中发挥着举足轻重的作用，因此概念的学习不能以熟练背诵为标准，而应重视概念的理解. 只有理解，才能掌握其本质属性，才能应用其解决问题. 因此，在概念教学中，教师要从学情出发，采用不同的教学方法，以帮助学生巩固概念.

例如，“同旁内角”的概念过于抽象，学生理解起来有一定的难度，于是教师结合图形让学生去寻找、去观察、去总结，从而领悟其本质属性. 这样不仅巩固了概念，也让学生对突破重难点有了信心.

问题1：图1中有几组同旁内角？

生1：两组，∠1与∠2，∠3与∠4.

师：说得很对，那么这两组角有什么共同特点呢？

生2：它们都在EF同侧.

生3：它们在两条线之间.

师：很好. 如果擦除构成∠1与∠2以外的线，你觉得剩余的线最像哪个字母？

生4：像字母“U”.

师：很好. 看来以后多了一种验证“同旁内角”的方法.

教学分析？摇 首先，教师设计了一个所有学生都够得着的问题来调动学生的积极性，即寻找图中的同旁内角. 学生找到两组同旁内角后，教师的教学没有结束，而是让学生仔细观察图形，并用自己的语言更加形象地总结其本质属性，让学生自己理解概念，因为自己理解和加工的概念应用起来会更加灵活. 此外，教师还让学生用字母“U”来形象地体会同旁内角，这不仅生动了课堂，还为以后观察复杂的图形做了铺垫.

突破表象，丰富外延

要想充分理解和掌握概念，只理解其内涵，而不懂其外延，那么对概念的理解可能存在偏差，从而引起错误. 概念的内涵与外延是相辅相成、相互依赖的，只有同等对待才能准确和全面地掌握概念.

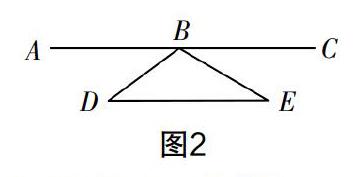
问题2：图2有几组同旁内角？

生5：根据上题的思路，AC，DE为两线，BE为截线，可以得到∠ABE与∠E是一组同旁内角.

生6：AC，DE为两线，BD为截线，可以得到∠CBD与∠D是一组同旁内角.

师：现在我们找到了两组同旁内角，是否还有其他同旁内角呢？（大多数学生都找到了两组，教师以问题为指引，让学生再仔细观察）

生7：∠DBE与∠E是不是也是一组同旁内角呢？

师：请详细说明一下.

生7：可以将DB和DE看作两条线，把BE看作截线.

师：很好. 谁来总结一下图2一共有几组同旁内角呢？

生8：一共有5组. ∠ABE与∠E是一组，∠CBD与∠D是一组，根据生7的思路，△DBE应该有3组同旁内角，所以总共5组同旁内角.

教学分析 ？摇根据“问题1”的思路，学生轻松地找到了两组同旁内角. 由于学生对概念的理解局限于单一的两条不相交的直线被一条直线相截的情况，而忽视了两条直线相交的情况，所以在寻找△DBE中的同旁内角时，陷入了思维定式. 这说明学生对概念外延的理解还不够深入，思维仅停留于表象，而未关注其本质，从而限制了思维的发展. 当学生出现思维定式时，教师应适时地引导，并留给学生足够的时间去体会，从而突破两条直线不相交的局限. 因此，教师要在概念内涵学习后，通过巧妙的变化，让学生突破固定思维的束缚，充分地掌握其外延，加深学习的深度，拓宽学习的广度，从而提升学生解决问题的效率.

类比归纳，化难为易

通过特殊发现一般规律是学生学好数学所必须具备的能力之一，有所发现才能有所收获，有所收获才能有所提高，这是学习所必须经历的过程.

例如，为了让学生充分地掌握同旁内角的外延，教师采用了类比法，即由三角形和四边形的同旁内角数量来推导n边形有多少组同旁内角，从而有效地将知识进行串联，化难为易，使知识学习更具程序化，使思维更具系统化，使学习变得更有趣.

问题3：请绘制一个三角形和一个四边形，看看各有几组同旁内角. （有了上面外延的扩展，学生很快有了答案）

生9：三角形有3组同旁内角.

师：如图3，我们将三角形和四边形的各边都延长，它们是不是就转化为我们熟悉的图形了？（有上面题目的铺垫，学生直接说出了三角形有3组同旁内角，但是未对其内涵有更加深刻的理解，此时教师及时进行引导）

生10：四边形有4组同旁内角.

师：如果是多边形，会有多少组同旁内角呢？

生11：我猜多边形有几条边就有几组同旁内角.

接下来，学生又继续验证了五边形和六边形，证明了该猜想的正确性. 解决完“问题1”之后，学生对概念的外延有了初步的认识，但未根深蒂固，在分析四边形有多少组同旁内角时产生了阻碍. 当数学语言解答问题过于抽象时，笔者借助圖3，用数形结合思想，使试题变得更直观，又将线段变为直线，转化为学生熟悉的图形，从而使学生解决问题变得水到渠成. 当学生得出三角形有3组同旁内角、四边形有4组同旁内角之后，笔者让学生探索多边形有多少组同旁内角. 借助类比、归纳等方法，学生总结出：若多边形为n边形（n≥3），则其有n组同旁内角.

教学中，教师通过精心设计，运用图形化难为易，并运用类比归纳、化特殊为一般等方法，让学生充分体验了类比、归纳的意义，为培养学生的创造性思维奠定了基础.

运用变式，培养发散思维

要培养学生的创新能力，可以有意识地添加或修改试题的条件，提升学生的应变能力和应用能力.

例如，为了激發学生的兴趣，培养学生的创新思维，师生共同探究问题“若添加一条对角线，对同旁内角的组数有何影响”，从而让学生运用已学的知识发现新知识，潜移默化地培养学生的发散思维.

问题4：如图4，连接四边形ABCD的对角线AC，图中共有多少组同旁内角？

师生共同分析：通过上面的问题，我们已经知道四边形有4组同旁内角，增加一条对角线后，就相当于增加了4个新角，而这4个新角与其同侧相邻的角组成一组同旁内角，同时本身这4个新角也组成了2组同旁内角，因此四边形多加一条对角线就多了6组同旁内角.

问题5：若是五边形和六边形，添加一条对角线后是否也增加了6组同旁内角？

运用归纳法，学生发现，任意多边形增加一条对角线后都会产生4个新角，4个新角只能与其相邻的角组成一组同旁内角，因此4个新角会产生4组同旁内角，加上4个新角本身构成2组同旁内角，因此n边形增加一条对角线后共有（n+6）组同旁内角.

教学中，采用师生共同探究的模式，可以有效地拉近师生的距离，探究从易到难、螺旋上升，能有效地发展学生的思维，同时运用类比、归纳的数学方法，能使学生的思维得到全面发展.

运用“跳一跳”，培养创新思维

让有能力的学生通过“跳一跳”来发展其创新思维，不仅是学习个体发展的需要，也是社会发展的需要. 只有通过“跳一跳”，才能让学生的思维从解决一个最近发展区问题跳到下一个最近发展区问题，从而提升学生的创新能力.

问题6：若n边形内有一点，请将该点与各顶点相连，则图形有多少组同旁内角？若该点在n边形外，又有多少组同旁内角？（可采用不完全归纳法进行验证）

分析：结合上面的问题可以发现，若四边形增加一条对角线，其增加2个三角形，而每个三角形有3组同旁内角，于是两个三角形有6组同旁内角. 五边形增加一条对角线，则将其分为一个三角形和一个四边形，三角形有3组同旁内角，四边形有4组同旁内角，但有1组重复，因此也是增加6组同旁内角. 学生可以从这个思路出发，将n边形分为多少个新的多边形，用数多边形同旁内角的思路去解题，这样会更加快捷. 该题比较复杂，不适合基础薄弱的学生，可以让有能力的学生“跳一跳”，从而不断提升思维能力.

总之，无论解决简单的试题还是复杂的试题，都要抓住试题的主要属性，寻找知识点之间的联系，通过总结和归纳构建完整的知识体系，从而提高学生解决问题的能力.