基于GeoGebra平台下对一道椭圆试题的探究与推广*

广东省中山市小榄中学 (528415) 李 琨

广东省中山市濠头中学 (528437) 闫 伟

圆锥曲线与直线的位置关系一直是高考的热点和难点，在很多圆锥曲线题目中都是探求一些特殊结论，这些结论看似特殊，实则都具普遍性，而且往往具有丰富的命题背景和深厚的内涵，研究此类试题不仅能够更好的把握解析几何的本质，还能透过试题挖掘隐含的命题规律，更能将其拓展到一般情况，从而提升学生数学思维,发展数学核心素养.下面笔者以复习备考中的一道椭圆试题的探究为例进行说明.

1试题呈现与分析

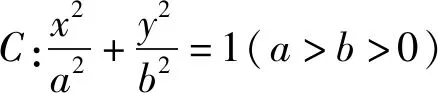
试题分析：本题主要考查椭圆的标准方程及其几何性质、直线与椭圆的位置关系、韦达定理以及椭圆中的动点轨迹和定值问题等内容，重点考查学生的推理论证能力、运算求解能力以及综合运用所学知识分析问题和解决问题的能力.试题结构清晰，问题设置层次分明，内涵丰富；试题第(2)问强化探究运算思路，选择运算方法，彰显数学运算和逻辑推理等核心素养，较好地检测了学生的学习潜能和数学素养.

2 解法探究

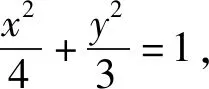
评注：设线法是比较自然的解法，设直线方程与椭圆联立并借助韦达定理进行参变量的代换，进而表示动点坐标，然后确定两条直线方程利用交轨法定Q点轨迹为一个圆，进而得到目标点H即为该圆的圆心.

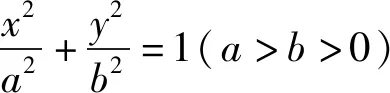
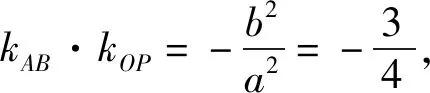
评注：解法2巧妙借助中点弦的斜率性质，从直线斜率角度来确定直线OP与直线EQ的位置关系得到Q点轨迹进而锁定目标点H，不仅体现了问题的本质，同时极大简化了推理运算过程，实现高效解题，要求学生对重要结论的积累和灵活运用.

3 基于GeoGebra的探究及反思

通过以上的分析和解答，直线OP与直线EQ的交点Q在定圆上，从而所求点H即是定圆的圆心那么该结果是偶然还是必然呢？两直线交点的轨迹和题目中椭圆的参数OP,EQ以及直线OP,EQ的位置有关系吗？如果将参数OP,EQ以及直线OP,EQ一般化，又会得到什么结果呢？由于涉及到的运算和直线OP,EQ的方程较为复杂，探究两直线交点的轨迹有一定的难度，因此笔者借助于GeoGebra平台进行探究，通过实验演示来找到与上述参数相关的定曲线方程，同时为后面的代数证明提供更加直观的思路支持.

实验1 (1)在GeoGebra绘图中先设置两个“滑动条”控制变量a,b，输入x^2/a^2+y^2/b^2=1得到一个椭圆C；(2)输入框中输入焦点[C]，得到椭圆的右焦点F，过点F作直线与椭圆交于A、B两点，与y轴于点E；(3)利用中点工具作出A、B中点P并作直线OP；(4)利用工具栏作出过点E且垂直OP的直线交OP于点Q，点击跟踪点Q轨迹；(5)拖动直线AB观察点Q的轨迹(如图1).

实验2 (1)在GeoGebra绘图中先设置两个“滑动条”控制变量a,b，输入x^2/a^2+y^2/b^2=1得到一个椭圆C；(2)再通过“滑动条”设置一个变量t，作出点F(t,0)并过点y作直线与椭圆交于A、B两点，与y轴于点E；(3)利用中点工具作出A、B中点P并作直线OP；(4)利用工具栏作出过点E且垂直OP的直线交OP于点Q，点击跟踪点Q轨迹；(5)拖动直线AB观察点Q的轨迹(如图2).或者改变椭圆参数a,b及参数t继续重复上述操作，点Q的轨迹仍然是一条定曲线.

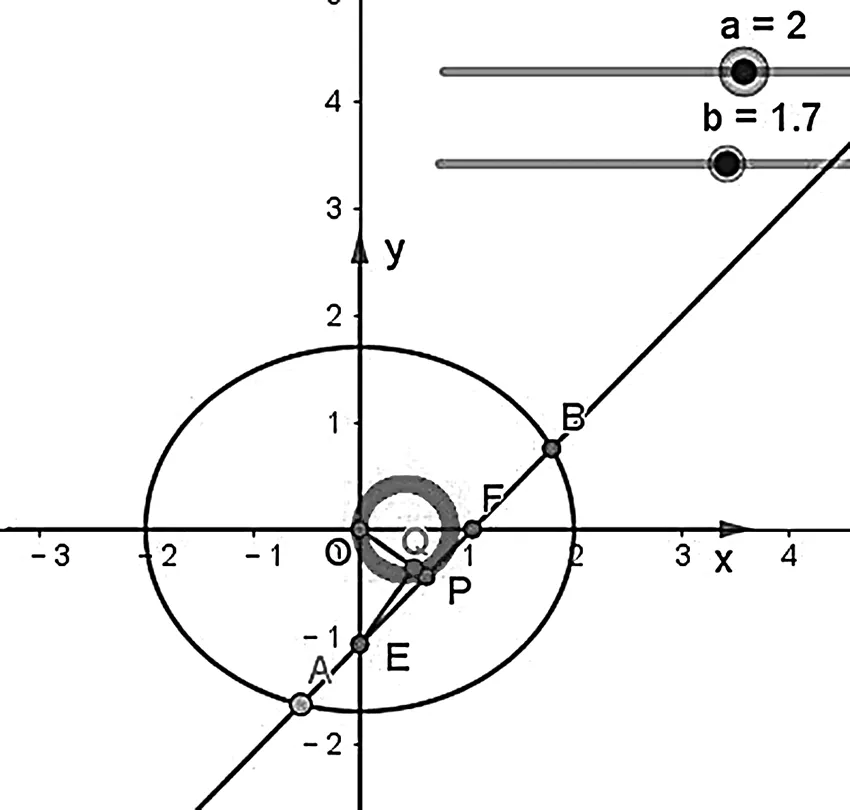
图1

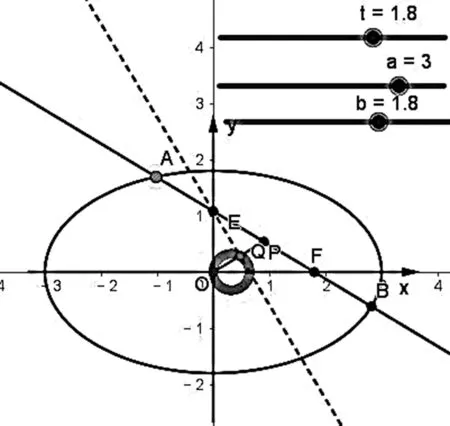
图2

根据以上实验的探究结果，师生可以直观认识到直线OP,EQ的交点Q恒在与参数a,b，t有关的定曲线上，于是我们可以将试题结论推广到一般情形：

4 推广结论 揭示本质

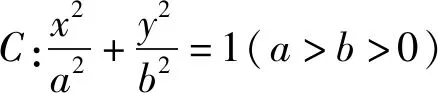
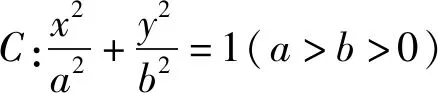
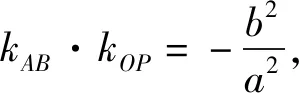
显然当t=c时，结论1是结论2的特例；若将椭圆换成双曲线，利用GeoGebra软件继续探究，经同样的实验操作，发现点Q的轨迹仍在定曲线上(如图3)，从而有如下结论：

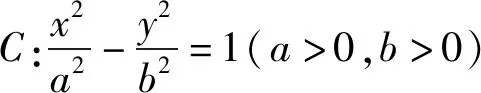
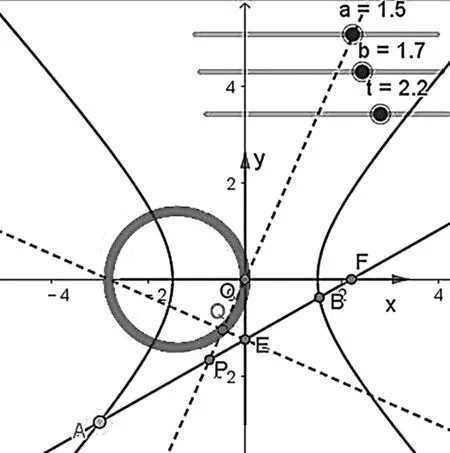
图3

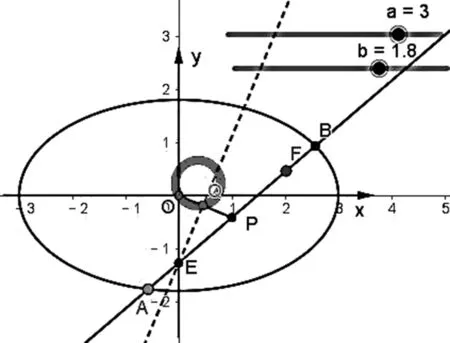
图4

由于椭圆和双曲线都是有心二次曲线，当点F是曲线内异于原点的任意一点时，按照上述实验2的操作步骤，拖动直线AB发现点Q的轨迹仍是一个定圆(如图4).从而进一步可以将上述结论统一为：

结论4 过有心二次曲线C内异于原点的一点F作一条斜率不为零的直线交曲线C于A、B两点，交y轴于点E，P为弦AB中点，过点E作直线OP的垂线交OP于点Q，则点Q的轨迹是一个定圆.

结论3和结论4的证明过程与结论2相仿，此处不再赘述，留给有兴趣的读者.

5 探后反思 引领教学

《普通高中数学课程标准(2017)》明确指出，“提升信息技术的使用能力，通过信息技术与课程的深度融合以及课程资源开发的多样化实现”.这就需要合理运用信息技术，以此提高数学教学的有效性.在本文的探究中，运用GeoGebra技术制作椭圆模型，再通过控制变量不断改变动直线和方程参数来演示图形变化过程，让学生观察所求动点的轨迹的运动情况，进而将实验结果拓展到有心二次曲线的统一结论，不仅为学生理解试题本质创设教学情境，而且为学生探索试题规律启发思维，为学生解决数学问题提供直观的思路支撑，而且实现了数学对象的多元表征(数字、表达式、图形等)，使得抽象的数学知识变得形象直观，有助于培养学生直观想象等核心素养[1].