一道三角最值问题的解法探究*
江苏省南京市金陵中学 (210005) 郭建华
求解与解三角形有关的最值问题时,正弦定理和余弦定理是解题的关键,基本不等式和导数是解题的工具.下面,笔者以一道三角最值问题为例,从题目条件表征的多个维度探寻解题的突破口.以此让学生体会解决该类问题方法的多样性和灵活性.
题目在△ABC中,内角A,B,C所对的边分别是a,b,c,已知acosB=6,c=4,则C的最大值为.
要解决这个题目,可以让学生作如下思考:它是一个什么问题?它要求的是什么?现在有哪些材料?有哪些工具?还需要哪些条件?还缺少哪些条件?能否从现有的条件中寻找?如何用这些条件和结论?是否还有其它条件可有利用?如何利用?等等.
本文给出以下四种解题思路,并简要分析每种解题思路中条件表征的形式和解法的获得.
思略1整体代换

评注:结合题设条件和求解的目标,很容易想到利用余弦定理进行边角互化.为求角C的最小值,先用余弦定理将cosB代换,得边a,b满足的关系式,再利用减元思想将cosC表示为关于边b的一元函数,最后结合基本不等式求cosC的最小值即可.
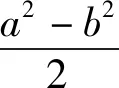
评注:对a2-b2=32,巧妙利用c=4的代换,探寻边a,b,c之间的关系,通过减元思想,将cosC表示成关于边a,b的二元函数,再利用基本不等式求cosC的最小值即可.
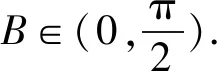
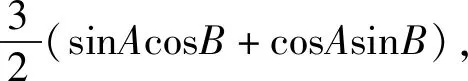
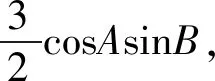
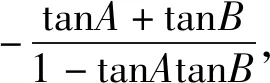
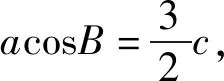
思路2射影定理

评注:由acosB联想到三角形中的射影定理acosB+bcosA=c,挖掘其隐含的条件bcosA=-2,再结合条件的结构形式,便可迅速找到解题的突破口.
思路3化斜为直
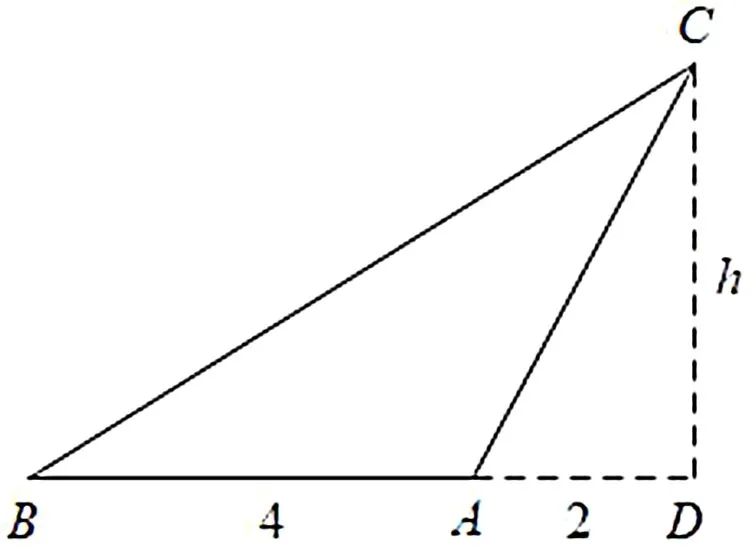
图1
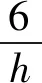
评注:由bcosA=-2,得线段AC在直线AB上的投影长为2,将斜△ABC补成Rt△BDC,即化斜三角形为直角三角形,更容易表达目标∠ACB=∠BCD-∠ACD,再结合两角和差的正切公式和基本不等式求解.
思路4夹角公式
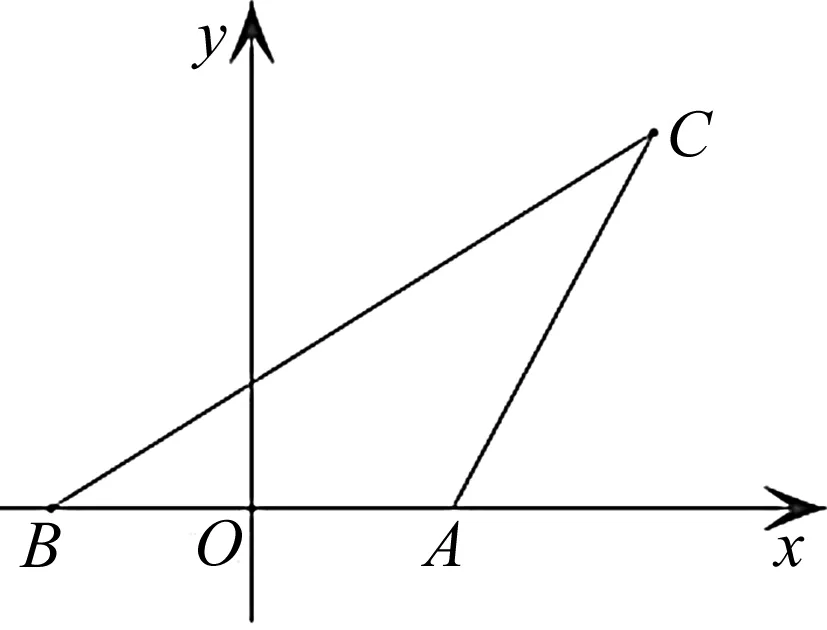
图2
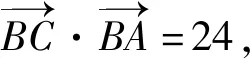
评注:充分整合条件acosB=6,c=4,联想数量积公式,通过建立适当的平面直角坐标系,探究动点C的轨迹(为一条定直线l),再结合向量的夹角公式求解.
只有深刻理解题意,才能充分整合题设条件,准确表征条件,并挖掘其隐含条件,多维度探究解决问题的突破口,将学生所学的知识融会贯通.利用一题多解,深化学生对理解基础知识、基本技能、基本思想、基本活动经验,提高从数学角度发现和提出问题的能力、分析和解决问题的能力,促进学生实践能力和创新意识的发展.

