Classical-field description of Bose-Einstein condensation of parallel light in a nonlinear optical cavity*

Hui-Fang Wang(王慧芳) Jin-Jun Zhang(张进军) and Jian-Jun Zhang(张建军)

1School of Chemistry and Material Science,Shanxi Normal University,Linfen 041004,China

2School of Physics and Information Science,Shanxi Normal University,Linfen 041004,China

Keywords: parallel light,Bose-Einstein condensation,quantum phase transition,collective excitation

1. Introduction

Bose-Einstein condensation (BEC) can be defined as macroscopic occupation of the ground state at thermal equilibrium. It is a common quantum property also a natural consequence of the statistics of many-particle boson system.Since its theoretical prediction,[1]the phenomenon of BEC has been observed in a wide variety system,[2-8]from ultracold atomic gases, to quasiparticles such as polaritions, excitons,and magnons. Photons have played a vital role for the experimental realization of BEC of these particles. We all know that photon is a boson. Considering the bosonic nature of photons,it is natural to ask if photons can also undergo a BEC.

In recent years increasing efforts have been made to investigating the equilibrium processes that lead to macroscopically occupied photon state. The difficulty is for usual photongas-like blackbody radiation, photons can be brought to thermal equilibrium, but the temperature and the photon number cannot be turned independently, which implies that for these systems the photon number is not conserved and the chemical potential is not well defined. However,the situation is different for the two-dimensional (2D) photon system. Recently,a photon number conserving thermalization process has been observed in a 2D optical microcavity.[9,10]In the experiment,the microcavity provides an effective mass and a nonvanishing chemical potential for photons which establish the condition for parallel light to achieve the BEC.

Recent process in research into BEC of photons has been made theoretically[11-18]and experimentally.[19,20]The statistical properties and the nonequilibrium model of photons in the BEC phase have been investigated.[21-24]Also,the superfluid state was observed in experiment based on the BEC of photons.[25,26]Furthermore,photons interact through an intermediate medium, e.g., photonic lattice and plasma have also been investigated.[27-30]

It is well known that the Kerr-like nonlinear medium is a very important“laboratory”to study the quantum properties of photon gas. In this article,we aim at describing the Bose-Einstein condensation of parallel light in the 2D nonlinear optical cavity using the classical-field method.First,the coupling model is presented to illustrate the propagation of parallel light in the nonlinear medium. Using the classical-field method,we furthermore derive a coupled density equation based on which the chemical potential and the quantum phase transition of the system are investigated. We also investigate the element excitation of the coupling system. Furthermore,we also discuss the question how the spontaneous decay of an atom is influenced by both the phase transition and collective excitation of the system.

2. Model and Hamiltonian

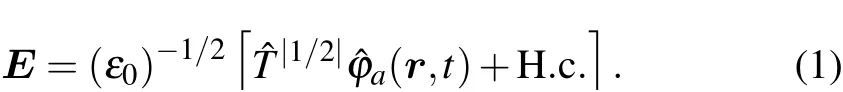
Fig. 1. Scheme of the optical micro-cavity. The micro-cavity consists of two high-reflecting curved-mirrors which provide an effective mass and a trap potential for photons.

In this letter, the parallel light is restricted into a twodimensional (2D) optical cavity as shown in Fig. 1, in which the field modeEhas the quantum form(with¯h=1 throughout this article)as follows:cause an effective photon-photon interaction. The interaction parametergphis given bygph=2g(3)(T0ph)4/(ε0)2. It should be emphasized that in this article we have assumed that the medium is isotropic and we have also considered that the system is in the BEC phase.Thus the differences of these parameters in the condensate phase and the general phase are ignored,and we treat them all as adjustable constants.

3. Classical-field description of the condensate phase

3.1. Description of the condensate wavefunction

It is well known that for an ideal Bose gas at absolute zero temperature, Bose-Einstein condensation is a common quantum property. According to previous analyses we know that this feature should also survive in our present coupling system. In the BEC phase,there exists a macroscopic numberN0of particles consisting of photons and p-molecules with the relationN0=Na0+2Nb0occupying the ground state at thermal equilibrium. The existence of a macroscopically populated state motivates splitting the field operator into two parts:a part with macroscopic matrix elements and a remainder,which accounts for supracondensate particles. The usual method proceeds by splitting the field operators according to

whereQa(t) is given byQa(t)=1−|φa〉〈φa|. To simplify the expression the operand°is introduced, which describes the action of an operatorOonto a field operator such as ˆψ(t):O°ˆψ(t)=∫dsO|s〉ˆψ(s,t). With the notation we can rewrite Eq.(12)and(14)as the simpler form

3.2. Derivation of the coupled density equation

From the description of the annihilation operatorβ(β=a,b)andδˆϕβ(r,t),we can obtain〈β+δˆϕβ(r,t)〉=0. Inspired by the result, in this section we introduce the decomposition operators ˆΛaand ˆΛbas follows:

3.3. The chemical potential and the quantum phase transition

To better visualize the phase transition,it is useful to plot the phase-space structure evolution of the chemical potentialµ. The results are shown in Fig.2. Two fixed pointsµminandµmaxcan be observed from Fig. 2. The fixed points on the phase space correspond to the minimum and maximum ofµ.It is found that for the case ofTeff<1,with the increase ofTeff,µminmoves smoothly along the lineθ=0 towards the phase boundaryρ=1 while the maximum approachesρ=−1. Especially, across the critical pointTeff=1 the system follows the minimum point and finally reachesρ=1, implying the entire conversion of photons into p-molecules,i.e.,the system transforms into the pure p-molecules condensate phase.nalizing the Hamiltonian(9)numerically in the Hillbert space with Fock basis:

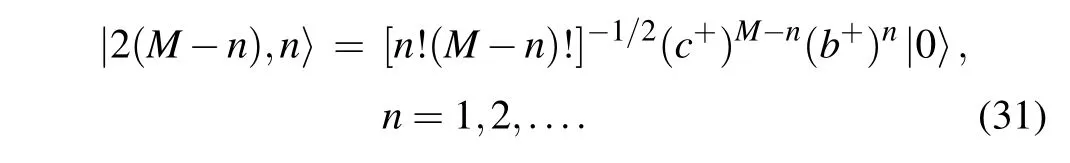
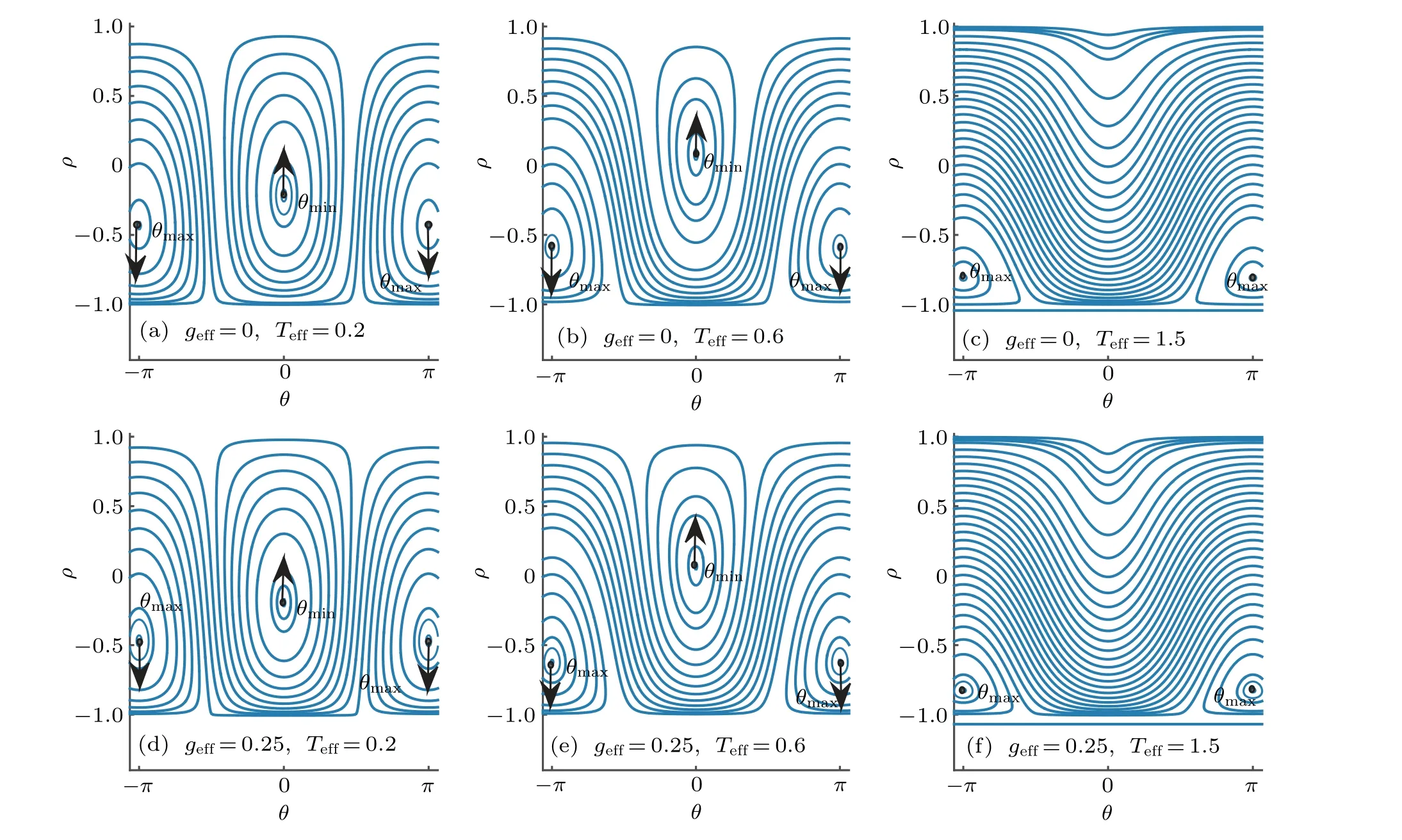
Fig.2. The phase space evolution of the chemical potentialµ as Teff changes. The arrows indicate the shifting direction of the fixed points as Teff increases. Here,µ is scaled byχN,we also defnie geff=gN/

Fig.3.Particle densities of photon and p-molecule in the ground state as a function of parameter Teff.Here,we set N=2000 and gN/=0.

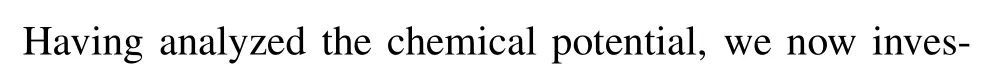
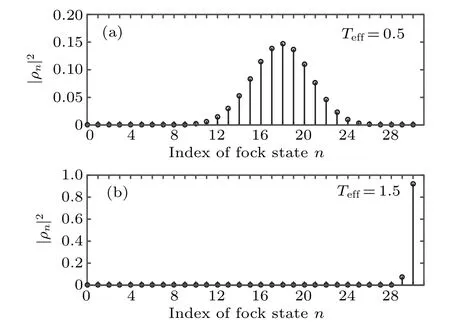
Fig.4. The probabilities of the system occupying different Fock states.Here,we set N=60 and gN/=0.

4. The spectrum of collective excitations

4.1. The photon and p-molecule condensate phase

We know that the time evolution of the small perturbationsδˆϕaandδˆϕb,that is the dynamics of the noncondensed particles, describes the elementary excitations of the system.From the definition ofδˆϕaandδˆϕbgiven in Eqs. (14) and(15),we can obtain the dynamics equation of supracondensate wavefunctions

whereδLis given by

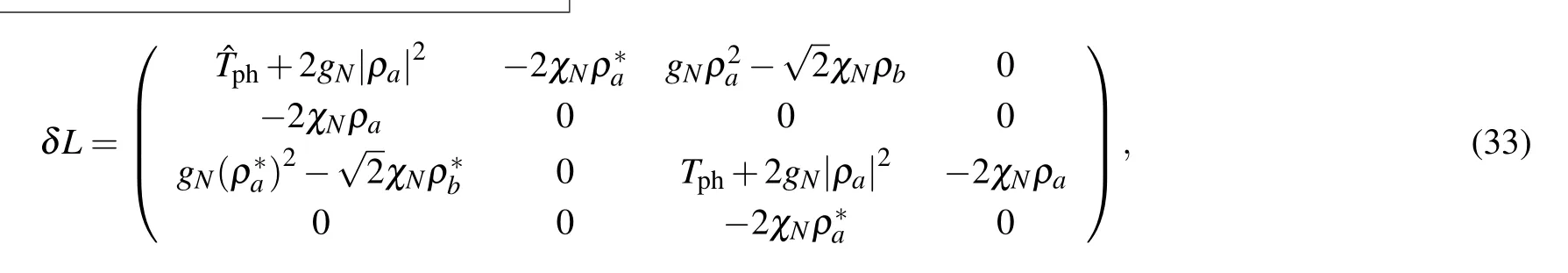
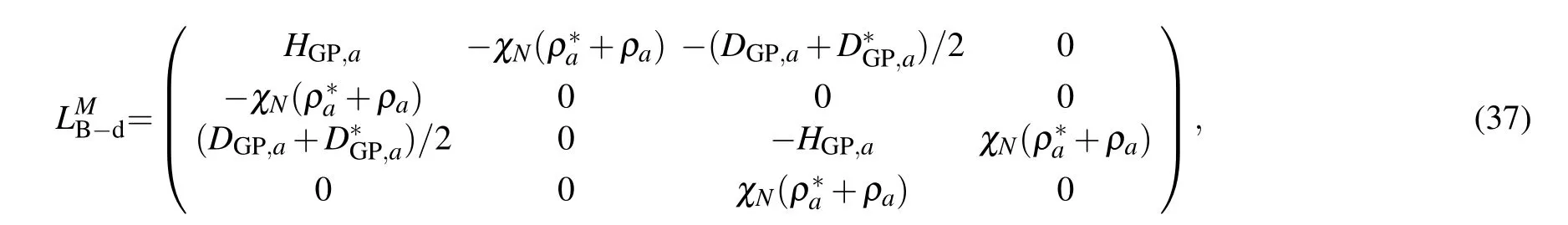
Figure 5 shows the quasiparticle dispersion spectra(in the limit of weak photon interaction,gN/χN ≪1). As can be seen clearly in the figure, the photonic excitation energyωais smaller than the excitation energyωbfor p-molecule. We also find that the energy to create a photon-dominated quasiparticle decreases withρ. The above results reveal that with the increase of the p-molecule conversion rate the collective excitation of the system is mainly contributed by the noncondensate photon modes.

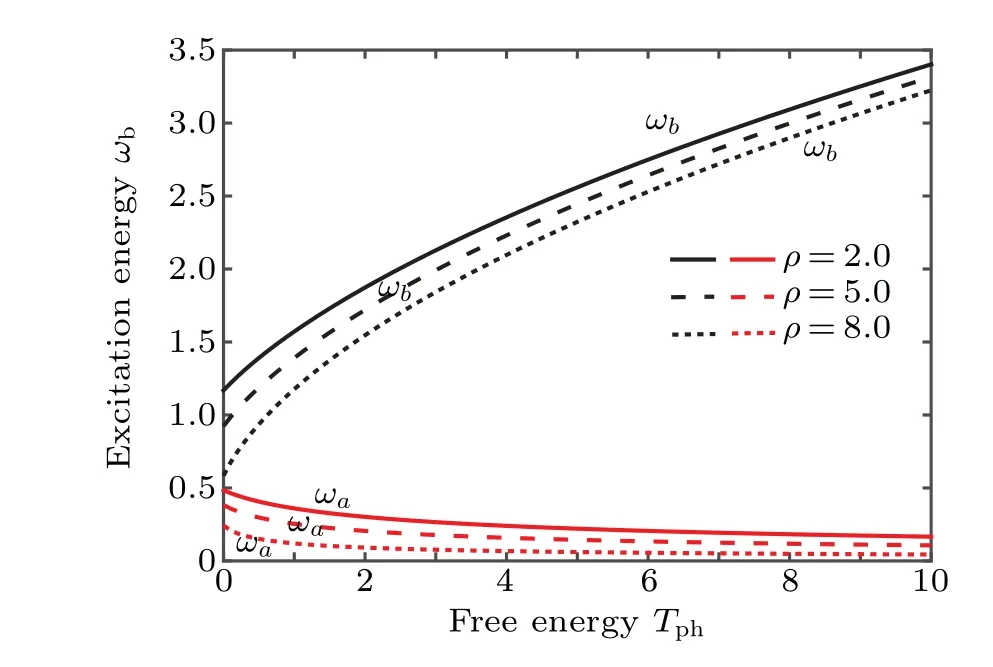
Fig.5. Illustrating the shape of the spectrums of elementary excitations in the mixed photon and p-molecule condensate phase for different values of the density difference ρ.Here,the free energy Tph of photons and the excitation energy ωβ(β =a,b)are scaled by χN,and we also set gN/=0.

4.2. The pure p-molecule condensate phase

The expressions for the excitation spectrum and the factorsua,krandva,krare analogous to those for a superconductor in the BCS theory,apart from some sign changes due to the fact that we are here dealing with bosons rather than fermions.The dispersion relation here also implies the existence of superfluid phase of photons.

5. Atom inside the micro-cavity

5.1. The interaction energy between the atom and the radiation field

It is well known that a single atom is an ideal“laboratory”to study the quantum properties of the radiation field. We have also known that in the experiment of the BEC of paraxial light,there exists continuous absorption and emission of photons by the dye solution to maintain the conservation of photon number. Therefore, it is necessary to investigate the atom-light coupling in the present model. In this section, we consider a two-level atom immersed inside the microcavity.The coupling interaction between the atom and the radiation field consisting of photons and p-molecules can be described by the following Hamiltonian(in the second quantization representation):

5.2. Spontaneous decay of the atom

In the present model, we assume that the transition frequencyωegbetween the two atomic levels is enough large so that only the spontaneous decay of the atom needs to be considered. To analyze the process of spontaneous decay,we also assume that the atom initially is in the excited state|e〉and the quasiparticle field is in the vacuum state. This state can be written as|e,0,0〉. As time evolves, the atom has the probability to drop down to the ground state and the system emits a quasiparticle. Thus the time evolution of the quantum state takes the form

where the transition matrixMTis given by

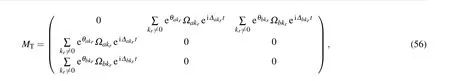
In this article we defineFb(t)as the damping force of photons.Equation(57)implies that in the mixed photon and p-molecule condensate phase,the spontaneous decay inducing by the coupling between the atom and the photon gas has the form of damped motion, and the damping force is related to the coupling between the atom and the p-molecules. Especially, as the system turns into the pure p-molecule condensate phase,the damping forceFb(t)=0. By substituting the expressions of the vacuum Rabi frequencyΩakrand the Bogliubov modified factor eθαkrinto Eq.(57), and transforming the summation into an integral form,the integral-differential equation forCe(t)can be obtained as follows:

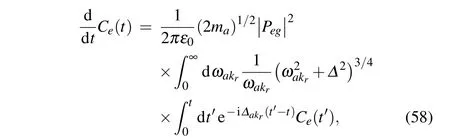
wherePeg=|e|〈e|r|g〉is real, and∆is the energy gap of the photonic quasiparticle given in Eq. (44). In Eq. (58), we notice that the major contribution to the integral overωakris from a small region centered aroundωeg,thus we can use the Weisskopf-Wigner approximation[42]and replaceωakrin the integral byωeg. We finally find in the pure p-molecule phase Eq.(58)has a simple form

Fig.6. Variation of the nonlinear decay factor ΓN with respect to the effective energy gap ∆*.Above,ΓN are scaled by ∆and ωeg,respectively.

From Eqs. (60) and (62), we find that obviously in the pure p-molecule phase the decay rateΓis an increasing function of the energy gap∆. The result is easily to understand.From the dispersion relation (44), we know that with the increasing energy gap∆, the excitation of the photonic quasiparticle becomes more easily. Consequently, the interaction between the atom and the quasiparticle field enhances,and the spontaneous decay of the atom increases. If we review the definition of energy gap given in Eq. (44), then we can find that the nonlinear factorΓNmainly comes from the convertion between photons and p-moleules. Furthermore,from Eq.(62)we have known that the nonlinear effect is also influenced by the transition frequencyωeg. In order to illustrate the dependency between the energy gap∆and the transition frequencyωeg, here we have also introduced the notion of effective gap∆*=∆/ωeg. The function relation betweenΓNand∆*is plotted in Fig. 6. From Fig. 6, we also find that for fixed energy gap∆, in the region ofωeg>∆the nonlinear factorΓN→1,which implies that in this region the nonlinear effect disappears. Thus, we have also defined∆as the critical transition frequency of the atom.

6. Conclusion

In our present model,photons confined inside the microcavity can be treated as usual massive bosons. Considering the propagation of the massive photon in the Kerr nonlinear medium, it is found that due to the nonlinear effect the massive photons are converted into p-molecules.In this article,we have first illustrated the coupling model consisting of photon and p-molecule. We have also considered that the coupling system is in the BEC phase. It is well known that the Bogliubov theory is a valid tool to analyze the condensate properties of the Bose gas. The theory should also be suitable to describe our present system. Using the classical-field method,we have furthermore proposed a coupled density equation that can be used to describe the conversion relation between photons and p-molecules. Based on the density equation,we have obtained the chemical potential,and we have also investigated the quantum phase transition of the coupling system. The results show that in the ground state the current system can transform from the mixed photon and p-molecule condensate phase into the pure p-molecule condensate phase. Furthermore,we have also calculated the collective mode and the spectrum function of the collective excitations.

Subsequently, we have considered the question how the spontaneous decay of an atom is influenced by both the phase transition and collective excitation of the system.By introducing the Bogliubov transition we have found that a correction factor can be obtained, which turns the interaction between the atom and the radiation field into the interaction between the atom and the quasiparticle field. Especially,in the pure pmolecule condensate phase,we also find that the spontaneous decay of the atom is influenced by the energy gap∆of the quasiparticle,and it is an increasing function of∆.

Appendix ASubstituting Eqs.(A2)and(A3)into Eq.(A1),we can find the time derivative of ˆΛain the following form: