不同坐标系下傅立叶变换性质
李盘润 刘 瑶
(四川信息职业技术学院,四川 广元 628000)
傅立叶变换作为一种线性积分变换,在物理学及工程技术有许多应用,通常将时域信号转变为频域信号,分析信号的频域成分。对于简单的时间信号。通常仅考虑一个维度的信号变化,即一维傅立叶变换。近年来,图像处理技术越来越多采用傅立叶变换技术,而空间上图像不再是简单的一维信号,可以由一维推广获得二维傅立叶变换。对于更高维信号,同样存在高维傅立叶变换。
本文主要针对二维傅立叶变换进行研究。在笛卡尔坐标系下,在空间上对信号做采样处理,将连续傅立叶变换(CFT)转换为离散傅立叶变换(DFT),进而容易在数字计算机上进行计算。而对于某些中心对称函数,更容易在极坐标上描述,则需要定义在极坐标上傅立叶变换,如傅立叶光学。此时采样信息为极坐标采样,因此不能够采用离散傅立叶的快速算法。而极坐标上采样可以认为是一种非均匀采样方法,进而可采用NEFT 实现极坐标采样条件下的离散傅立叶变换计算。但对于一些特殊的极坐标函数,容易获得相应连续傅立叶变换的解析解。
本文将针对不同坐标定义下的连续傅立叶变换进行研究,并给出关于连续变换与离散变换及非均匀变换之间的关系。进一步针对某些理想区域上的特殊函数,利用傅立叶变换积分定义,容易计算相应傅立叶变换的原函数。对于特殊的高斯函数,计算其对应的傅立叶变换对。
1 积分变换定义
本节给出不同坐标系条件下,二维傅立叶变换的定义,同时,给出一维Hankel 变换,在后面的内容中,二维极坐标上的傅立叶变换可转为一维Hankel 变换。
1.1 笛卡尔坐标系傅立叶变换
笛卡尔坐标下,函数f(x,y)在[-∞,+∞]有定义,且满足傅立叶积分定理条件,则函数:
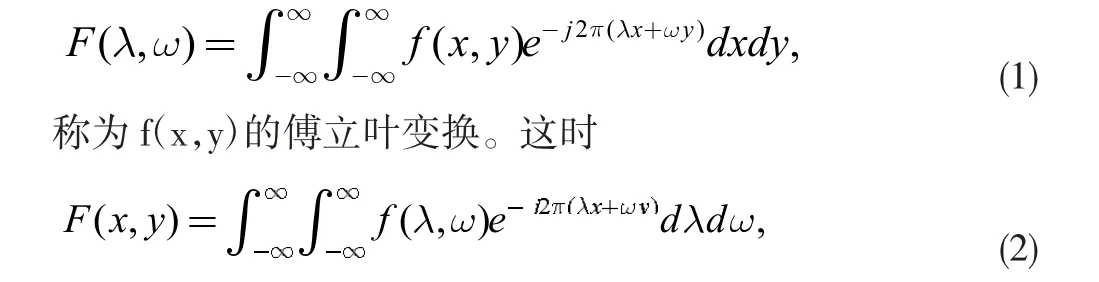
称为f(λ,ω)的傅立叶逆变换。
f(λ,ω)称为f(x,y)在傅立叶变换下的象函数,反之,称为原函数。象函数与原函数构成一组傅立叶变换对。
1.2 极坐标系傅立叶变换
对于某些二维函数,具有中心对称的性质,相比与笛卡尔坐标系,该函数更容易在极坐标系上描述。在极坐标下,设空间域函数,其对应域上的傅立叶象函数为F(ρ,φ)。则傅立叶变换的形式如下:
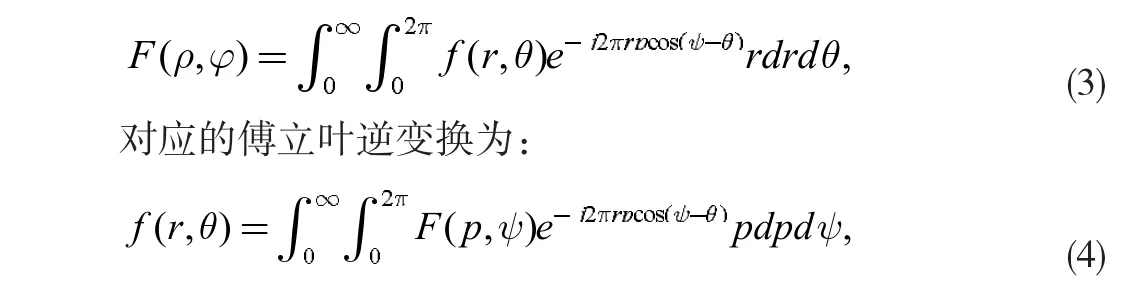
极坐标系的傅立叶变换定义与式(1)与式(2)等价,象函数与原函数构成一组傅立叶变换对。关于两种定义的等价关系,可通过积分的变量替换方法实现证明,此处不做详细说明
1.3 Hankel 变换
Hankel 变换为另一类积分变换,n 阶Hankel 变换定义为如下积分:
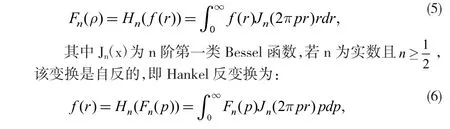
极坐标上的二维傅立叶变换,可通过一维上的Hankel 变换描述,从而容易计算极坐标上的傅立叶变换对。
2 离散傅立叶变换
在笛卡尔坐标系上,式(1)通常为连续傅立叶变换。为使该积分变换的计算能在计算机上进行,需将式(1)连续傅立叶变换转为离散傅立叶变换。若f(x,y)在x=nT,y=mT(n,m=0,±0,±1,±2,…)是连续的,称f(nT,mT)为采样间隔为T 的采样波形。其对应的离散傅立叶变换为:
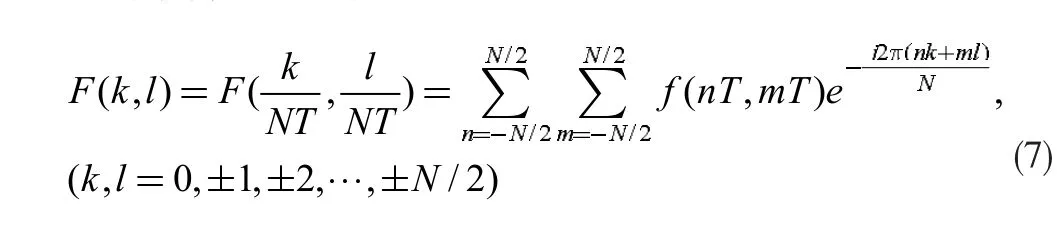
根据采样定理,频域上采样间隔δf=1/NT,关于上式存在快速计算方法(FFT),需要注意离散傅立叶变换空间采样及频域采样存在极强的耦合关系。
在研究过程中,任意函数关于(1)的连续傅立叶变换不存在耦合关系,但其直接积分计算,需记住黎曼积分计算频域上特定位置的象函数:
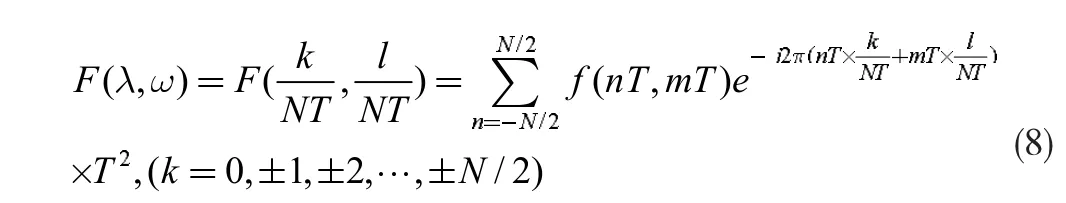
比较(7)与(8),即连续傅立叶变换与离散傅立叶变换的频域振幅存在T2的倍数关系,从而可根据快速傅立叶方法(FFT)获得特定频域位置上的傅立叶象函数。类似简单推导可应用在逆变换上。
3 基于采样的非均匀傅立叶变换
式(7)为离散傅立叶变换,它的快速算法FFT 的计算复杂度为O(nlogn)。但是存在诸多限制,比如频域点与空间点存在极强的耦合关系δf=1/T,且必须在采样空间必须均匀采样。这些限制导致在应用中,如果使用FFT 算法,无法通过在频率域加密采样来提高空间域变换结果的精度。连续傅立叶变换,可以避免频域点与空间点的耦合关系及采样条件限制,但是需进行复杂且耗时的积分运算。存在基于采样的非均匀傅立叶变换。
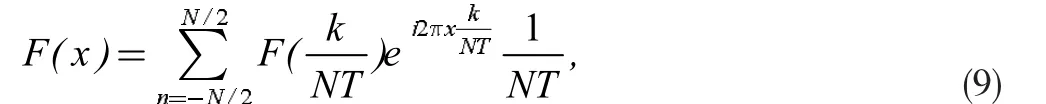
其中x 为空间上任意位置,从而避免的限制,其计算复杂度为O(n2)。对于频域均匀采样而空间域非均匀c 采样的非均匀傅立叶变换,同样存在快速计算方法[3]。
非均匀傅立叶变换的快速实现。其本质为连续傅立叶变化的离散化。对于离散采样精度直接影响空间域变换结果的精度,直接的办法可通过在频率域加密采样,提高计算精度。对于某些函数F(p),若采样结果F(pi)=0。则加密采样的同时。会增加计算的时间,但对于精度的提升有限。另一种方法是提高频域采样精度,取采样结果为F(pi)采样对应区域与F(p)有效区域相交面积。该方法等价于在频率域加密采样,但仅选择特殊位置的采样结果去计算式(9),且该位置的采样结果为周围采样结果的均值。
基于采样离散傅立叶变换可获得特定位置(原)象函数值,而非均匀傅立叶变换容易获得任意位置的(原)象函数值。另一方面,极坐标上的采样可认为是笛卡尔坐标上的非均匀采样,从而极坐标上傅立叶变换容易通过非均匀傅立叶变换快速计算。
4 傅立叶变换与Hanker 变换的关系
本节中,着重说明极坐标条件下,连续傅立叶变换可表述为一维Hanker 变换的无穷级数。
4.1 径向对称函数
极坐标上某些径向对称函数(高斯函数等),仅需ρ 径向描述该二维函数,考虑极坐标系下的傅立叶变换定义(3);

对于径向对称函数,二维空间上的傅立叶变换,可通过一维的Hankel 变换计算。
4.2 径向非对称函数
根据文献[6],笛卡尔坐标系的傅立叶变换核存在如下级数展开式:

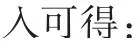

即傅立叶变换对中,空间函数的级数展开系数fn(r)与对应频域函数的级数展开系数Fn(ρ)存在倍数关系。
5 理想函数的傅立叶变换

5.1 多边形区域
若采样窗口大小为ω 和h,且对应频域采样点fn和gm分别为
则对于简单多边形区域,顺时针定义多边形区域Ω 的顶点(xi,yi),根据(1),对应的傅立叶变换:
5.2 圆形区域
针对理想函数,上节对于简单多边形区域,给出了笛卡尔坐标系下的傅立叶变换的计算过程。对于更一般的圆形区域,其傅立叶变换更容易在极坐标下的傅立叶变换实现积分计算。

6 结论
本文分别针对两种坐标系,分别考虑相应的连续傅立叶变换定义。在笛卡尔坐标系条件下,介绍了基于采样的离散傅立叶变换及非均匀傅立叶变换,通过数学描述与连续变换之间的关系。在极坐标系条件下,二维傅立叶变换容易通过一维上的Hankel 变换快速计算。并分别针对多边形区域、圆形区域的理想函数,根据傅立叶变换定义,计算相应的(原)象函数。最后,根据Bessel 函数性质,二维高斯函数容易在极坐标系上描述,根据相应傅立叶变换定义,容易获得空间及频域上的傅立叶变换对。
致谢:感谢审稿人提出的宝贵修改意见。

