一类带时滞和收获率的捕食者-食饵系统的稳定性

吴耀冲，温洁嫦*

（广东工业大学 应用数学学院，广东 广州 510520）

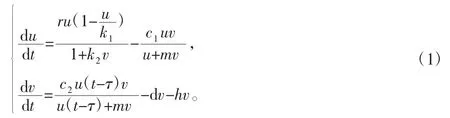
其中，u，v 分别表示食饵和捕食者种群密度；r，k1，k2分别为食饵的内禀增长率、环境对食饵种群的容纳量和食饵对捕食行为的恐惧系数；c1，c2分别为捕食者对食饵的捕获率和能量的转化率；ø（u，v）=为比例依赖型功能反应函数，且m 为半饱和系数；d，h 分别为捕食者的死亡率和收获率；τ为食饵种群孕育后代产生的时滞。考虑到现实意义，参数r，k1，k2，c1，c2，m，d，h，τ 均为非负数。

1 系统平衡点存在条件和稳定性分析

系统（1）存在一个边界平衡点E1（k1，0），和当c2＞d+h 时存在一个正平衡点E2（u*，v*），其中

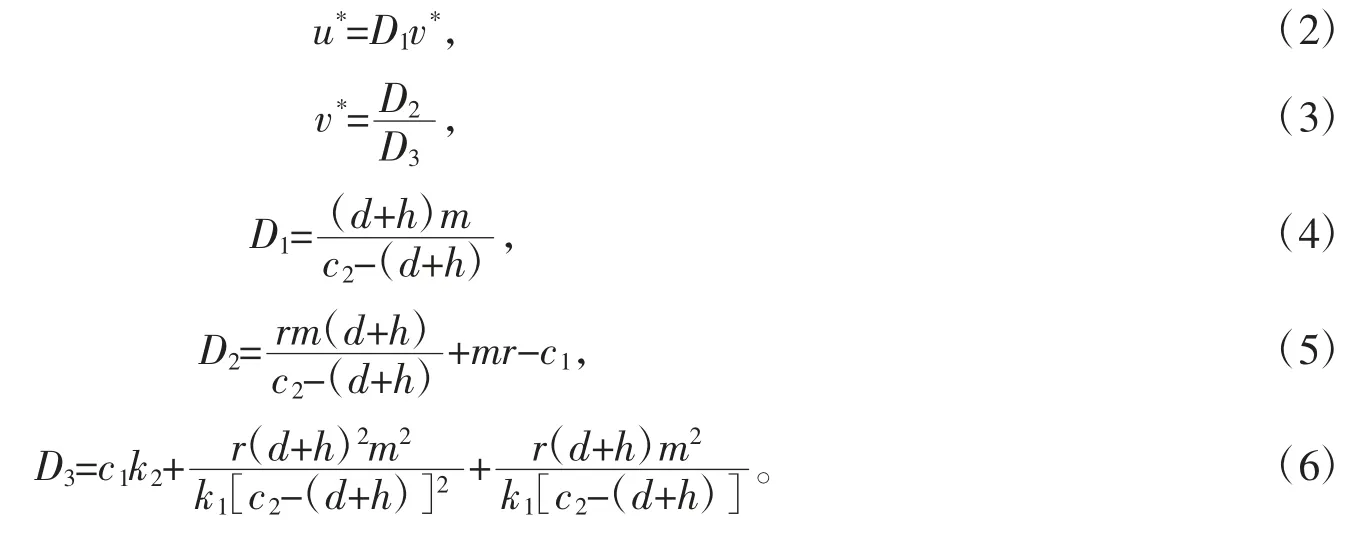
1.1 τ=0 时平衡点的稳定性

定理1当c2＜d+h 时，边界平衡点E1局部渐近稳定；当c2＞d+h 时，边界平衡点E1不稳定。

证明系统（1）在E1处的Jacobi 矩阵为

定理2当时，E2是局部渐近稳定的平衡点。

证明系统（1）在E2处的Jocobi 矩阵为

伴随着移动互联网技术的蓬勃发展，移动支付正在改变支付结算方式，为电网企业物资合同结算管理效率提升提供了新思路[4]。

其中

1.2 τ≠0 时平衡点的稳定性

对系统（1）在E2处作线性化处理，得

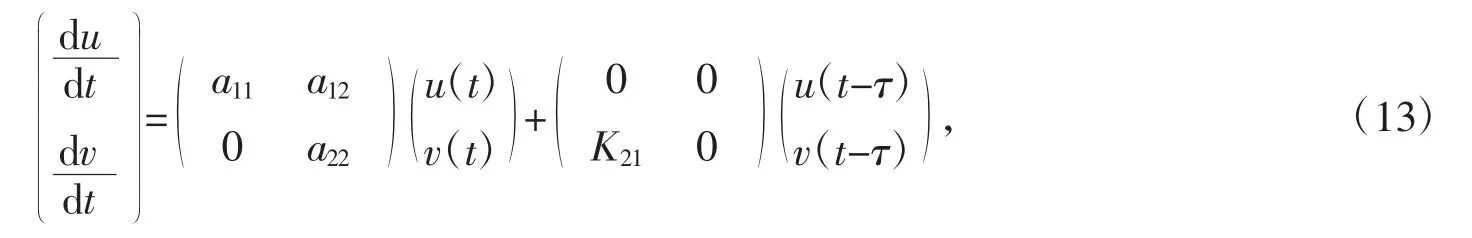
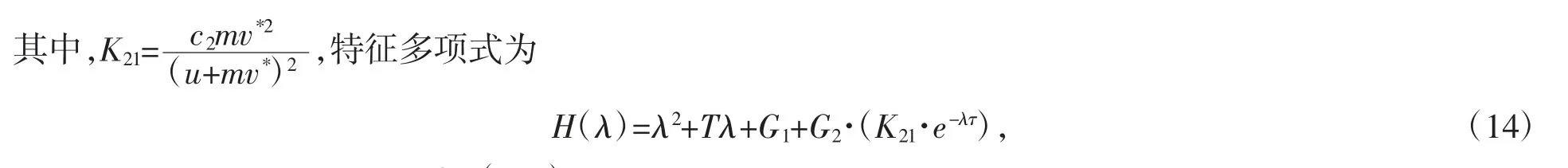
其中，T=-（a11+a22），G1=a11a22，G2=（-a12）。

定理3当τ≠0 时，c2＜d+h 时，E1局部渐近稳定。

证明在E1处，a11=-r，a12=-c1，K21=a21=0，a22=c2-d-h，当c2＜d+h 时，由Routh-Hurwitz 判据得多项式H（λ）所有特征根都有负实部，故此时E1局部渐近稳定。

令λ=iw 是方程（14）的一个根，对于τ＞0，有

分离实部和虚部，得

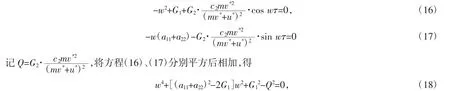
设W=w2，有

定理4由于（a11+a22）2-2G1＞0，根据Routh-Hurwitz 判据可知，当G12＞Q2时，方程（19）所有根都有负实部，故此时方程（18）的根没有穿过纯虚数轴，则平衡点E2局部渐近稳定。

当G12＜Q2时，方程（16）、（17）有一正根，即

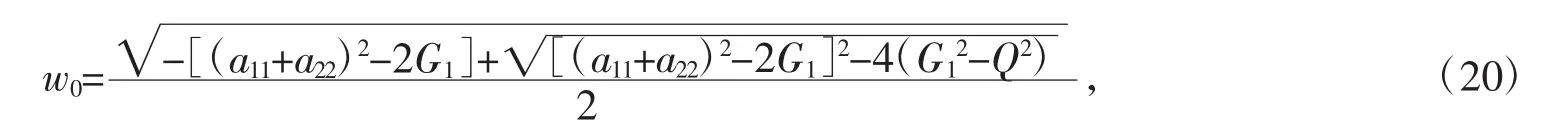
此时

这表明当τ=τ0时，方程（14）有一对纯虚数根λ=±iw0；当τ＜τ0时，平衡点E2局部渐近稳定。其中

下面验证横截条件［14］，即

由等式（14），得

所以当τ=τ0时，有

故横截条件满足。所以有以下结论：

定理5当G12＞Q2时，对于所有τ＞0，平衡点E2局部渐近稳定；当G12＜Q2成立，则τ＜τ0时，平衡点E2局部渐近稳定，当τ＞τ0时，平衡点E2不稳定，当τ=τ0时，系统在E2附近发生Hopf 分支。

2 数值模拟

当τ=0 时，即不考虑食饵种群孕育后代产生的时滞对系统的影响。取r=0.5，k1=11，c1=0.2，c2=0.07，m=0.1，d=0.03，h=0.05，k2=0.2，此时c2＜d+h 成立，从图1、2 可以看出，此时系统（1）中的捕食者和食饵种群数量不随时间变化而变化，但捕食者趋于灭绝，仅食饵种群长久存活下去。取r=0.5，k1=11，k2=3，c1=0.08，c2=0.05，m=1，d=0.03，h=0.01，满足，从图3、4 可以看出，此时E2为稳定的焦点，且系统中的两种群都随着时间的流逝而长久存活下去并未灭绝。

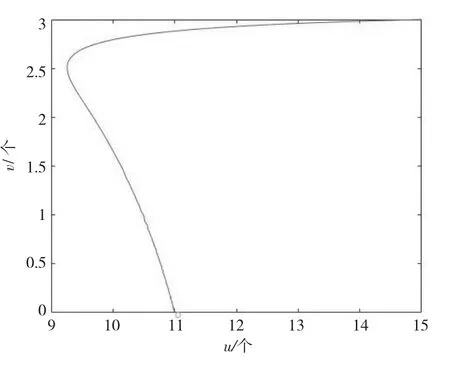
图1 E1 附近的轨线

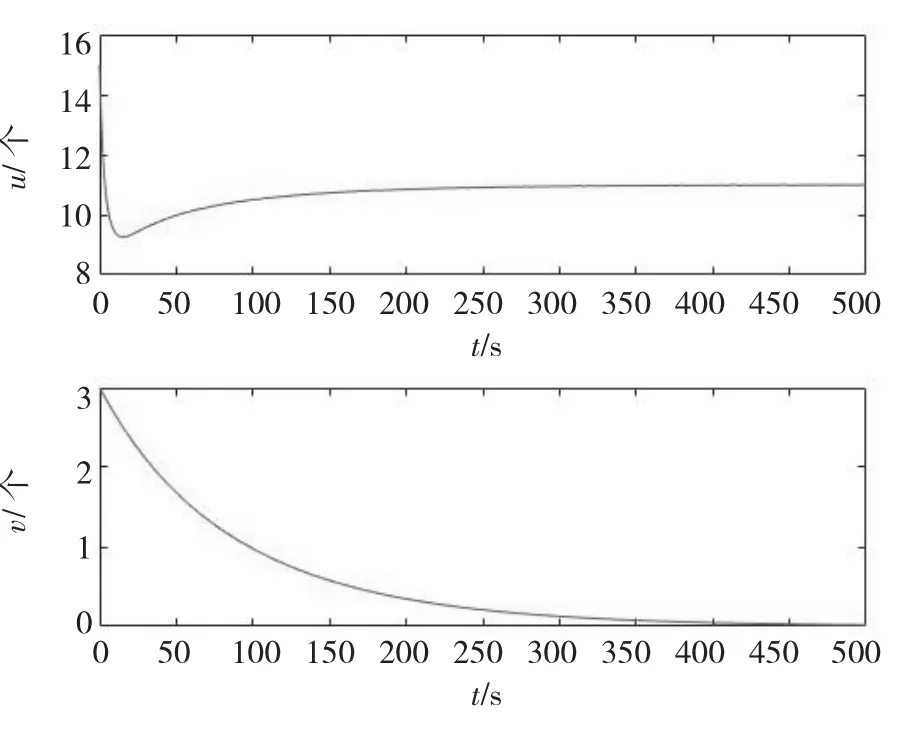
图2 E1 稳定时两种群密度

图3 E2 附近的轨线

图4 E2 为稳定焦点时两种群密度

考虑食饵种群孕育后代产生的时滞对系统的影响，此时τ≠0。取τ=4，r=0.5，k1=11，c1=0.2，c2=0.07，m=0.1，d=0.03，h=0.05，k2=0.2，满足定理3 的条件，此时系统中的捕食者灭绝，食饵种群长久存活（如图5 所示）。取h=0.02，初始条件及其它参数相同情况下，从图6 可以发现，系统变得不稳定，这说明在满足一定条件下，恰当的人为干预有利于系统（1）两物种的稳定。

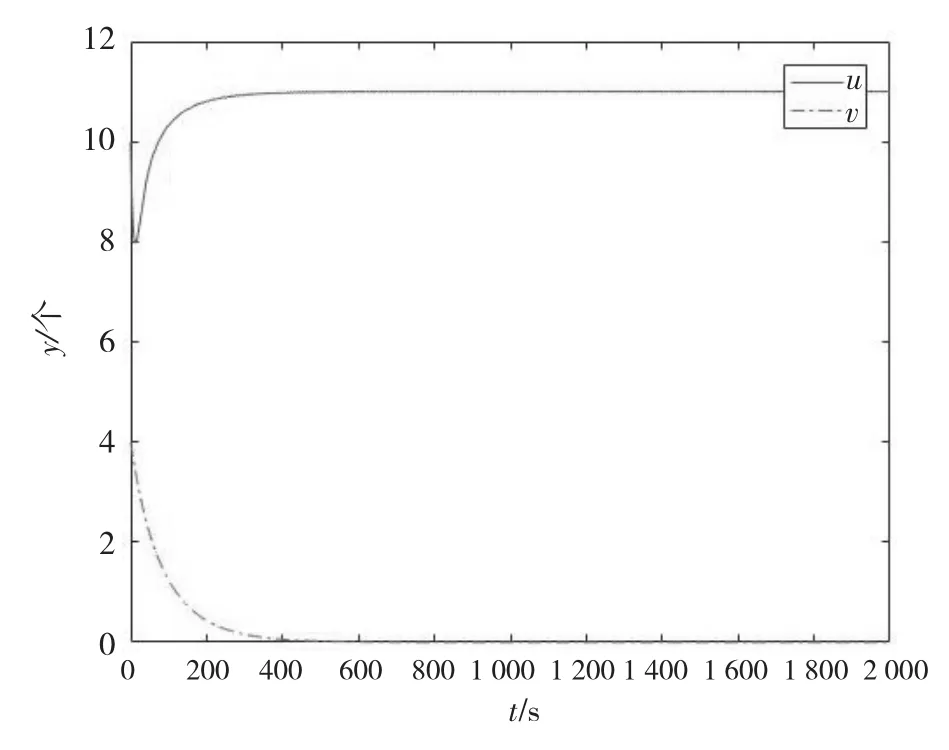
图5 h=0.05 两种群密度

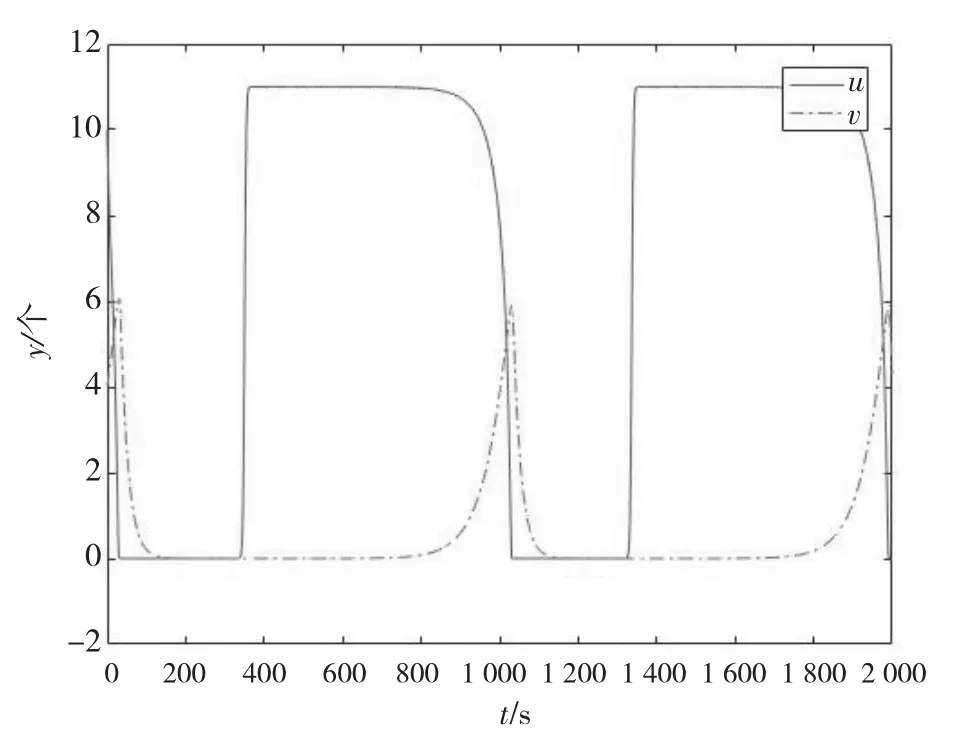
图6 h=0.02 两种群密度

取r=0.8，k1=11，c1=0.2，c2=0.1，m=0.4，d=0.03，h=0.05，k2=0.5，τ=10，此时系统（1）的捕食者与食饵种群都没有灭绝并且稳定存活（如图7 所示）。取r=0.5，k1=11，c1=0.08，m=0.8，c2=0.05，d=0.02，h=0.001，k2=2，τ=0.02，此时系统（1）在E2附近发生Hopf 分支（如图8 所示），捕食者和食饵的种群密度呈周期性变化，随着时间的流逝一直稳定存在且都没有灭绝。

图7 τ=10时两种群密度

图8 τ=0.02时两种群密度

3 结论

考虑了食饵种群孕育后代在时间上产生的延迟对系统的影响，从理论上证明了系统（1）的平衡点存在条件，利用Routh-Hurwitz 判据证明了两平衡点局部渐近稳定的成立条件，通过实验分析发现：1）时滞不能破坏E1的局部渐近稳定性质；2）在满足一定条件下，恰当的人为干预有利于系统（1）两物种的稳定；3）当τ=τ0时，系统在正平衡点附近发生Hopf 分支产生周期振荡。