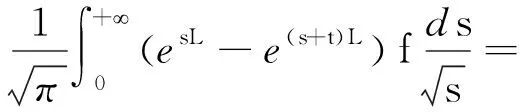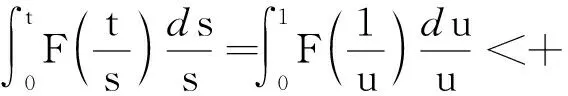对称马氏过程对应梯度型算子的弱(1,1)有界性
周博文,张龙腾
(1.福建师范大学 数学与统计学院,福建 福州 350007; 2.福建师范大学 协和学院,福建 福州 350007)
马氏半群的分析性质是随机过程与随机分析的主要研究内容之一,详见著作[1,2].这其中,对称马氏过程生成元的Riesz变换是一个非常活跃的研究课题.例如,在假定空间满足体积倍增条件下,文献[3,4,5]讨论了具有高斯型热核估计的对称扩散算子的Riesz变换;文献[6]在给定次高斯型热核估计情形下,建立了黎曼流形和图上Riesz变换的Lp有界性.上述四篇文献的证明方法强烈依赖于梯度算子的弱(1,1)有界性。然而,轨道不连续马氏过程对应非局部算子的Riesz变换至今仍未系统研究,部分结果可参见文献[7]中关于分数Laplace算子的研究。本文在狄氏型理论框架下,基于现有热核估计相关结果,建立了一般度量测度空间中对称马氏过程对应梯度型算子的弱(1,1)有界性.
1 预备知识与主要结论
本文在度量测度空间(M,ρ,μ)上讨论问题,其中μ是M上非负Radon测度且支撑为M.记B(x,r)={z∈M:ρ(x,z) (1) 其中V(x,r)=μ(B(x,r)). 特别地,由(1)可知,对任意x,y∈M,r>0,有 (2) 记R+=[0,+∞),令φ为R+上严格单调增函数,满足φ(0)=0,φ(1)=1及如下scaling性质: (3) 其中C1,C2>0为常数. 假设存在R+上有界递减正函数S,满足 (4) 其中d,α1,C1由(1)与(3)给出. 设(Pt)t≥0为L2(M,μ)上的对称马氏半群,其密度函数(亦称热核)为pt(x,y),即 (5) 其中Lp(M,μ)表示M上Lp-空间,其范数定义为 (6) 只需 〈f,(-L)f〉L2(M,μ), 定理1假设条件(A),(B)成立,其中 (A)热核pt(x,y)满足如下上界条件: (7) (B)(i)T具有次可加性且L2有界; (ii)存在(0,∞)上有界正函数F,使得 (8) 且 (9) 则算子T是弱(1,1)有界的,即对任意λ>0,f∈L1(M,μ)∩L2(M,μ),有 (10) 注1显然,若T满足弱(1,1)有界,则T是Lp有界的,这里p∈(1,2). 在给出定理1的证明之前,为便于论述先给出两个关键引理. 引理1对任意f∈L2(M,μ),t>0, (11) 其中: 进一步,若满足假设条件(B)- (ii),则 (12) 证明根据定义(6),对任意f∈L2(M,μ), 即有 即式(11)得证. 进一步,根据(8)可得 一方面,根据(9)可得 另一方面,利用F的有界性可知, 从而式(12)得证. 引理2存在常数c>0,使对任意t>0,x∈M,非负可测函数φ,有 其中:M为非中心Littlewood-Paley极大算子; (13) 一方面,由(7),S的有界性和体积倍增条件,对任意y∈B,有 (14) 另一方面,根据(7)与函数φ和S的单调性可知,对任意y∈B,j≥2,z∈Cj(B), 这样, (15) 其中,最后一个不等号利用 (2)和(4). 结合(13)及估计(14)、(15),有 由y与z的任意性可得所要的结论. 下面给出定理1的证明. 证明要证T满足弱(1,1)有界性,即需证明对任意λ>0,f∈L1(M,μ)∩L2(M,μ),有 根据著名的Calderón-Zygmund分解定理可知f=g+b[11].由T的次可加性可知,对任意λ>0, μ({x:|Tf(x)|>λ})≤μ({x:|Tg(x)|>λ/2})+μ({x:|Tb(x)|>λ/2}). 根据切比雪夫不等式、T的有界性及文献[11]可得 下面只要证明,对任意λ>0, (16) ‖bi‖1≤2n+1λμ(Bi) 和 记ti=φ(ri),则bi=etiLbi+(I-etiL)bi.由T的次可加性可知 (17) 注意到 (18) 由体积倍增条件及文献[11]定理可知 (19) 利用切比雪夫不等式及T的次可加性可得 为简单起见,省略下标i,记kt(x,y)为T(I-etiL)的热核.由supp(b)⊂B可知 再由引理1可得 从而 (20) 结合(18)、(19)和(20)可知 (21) 下面估计式(17)右边第二项.由切比雪夫不等式,对任意λ>0,有 (22) 根据对偶性和supp(bi)⊂Bi,有 (23) 进一步根据引理2及文献[11]定理可得 又利用Cauchy-Schwarz不等式,得 其中第一个不等式是根据上文构造球序列{Bi}i≥1所述M中每个点至多包含在2n+1个球Bi中这一事实. (24) 结合(22)、(23)和(24)估计,得 (25) 最后,根据(17)、(21)及(25),定理得证. 注2定理1的证明主要参考文献[10]命题3的证明,其思路源于文献[3,6]的讨论.文献[3,6]分别建立具有高斯、次高斯热核估计对称扩散算子对应Riesz变换的有界性.文献[10]命题3表明高斯或次高斯估计对建立Riesz变换的有界性是非必要的,即存在紧流形,在不具有高斯或次高斯估计条件下,其对应的Riesz变换是Lp有界的,其中1≤p<2.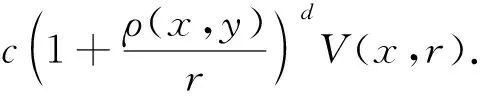









2 定理证明